课程传送门
L1 Overview of Computer Graphics
概述。不多讲。
L2 Review of Linear Algebra
线代复习,一些基本操作。不多讲。
变换。
直接上三维+齐次坐标版吧。
坐标\((x,y,z)\)表示为
\[\begin{bmatrix}
x\\
y\\
z\\
1\\
\end{bmatrix}
\]
以下所有矩阵使用时全部左乘在坐标矩阵上。
恒等变换(identity)
略。
平移变换(translation)
\[trans(d_x,d_y,d_z)=
\begin{bmatrix}
1&0&0&d_x \\
0&1&0&d_y \\
0&0&1&d_z \\
0&0&0&1
\end{bmatrix}\]
表示将坐标\((x,y,z)\)平移到\((x+d_x,y+d_y,z+d_z)\)
缩放变换(scaling)
\[scale(s_x,s_y,s_z)=
\begin{bmatrix}
s_x&0&0&0 \\
0&s_y&0&0 \\
0&0&s_z&0 \\
0&0&0&1 \\
\end{bmatrix}\]
表示将坐标\((x,y,z)\)缩放至\((x*s_x,y*s_y,z*s_z)\)
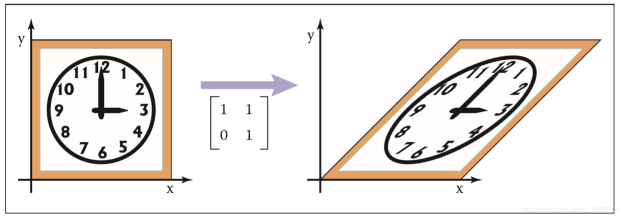
剪切变换(shearing)
这是对\(x\)轴作用的矩阵
\[shear(d_y,d_z)=
\begin{bmatrix}
1&d_y&d_z&0 \\
0&1&0&0 \\
0&0&1&0 \\
0&0&0&1
\end{bmatrix}\]
表示将坐标\((x,y,z)\)剪切至\((x+y*d_y+z*d_z,y,z)\)
可以想象为x轴被拉伸,其它轴不动。
二维的例子:
旋转变换(rotation)
注意,这里以右手系为例!
以下内容假定有对右手系和叉乘的认识

以下的绕某轴意思是:沿某轴正方向看过去,顺时针旋转多少
某轴正方向:从该轴负半轴取一个点,从该点指向原点
别问我为什么变成了顺时针,我也不知道
x->y(绕z轴)
\[rotate_z(\theta)=
\begin{bmatrix}
cos\theta& -sin\theta& 0& 0\\
sin\theta& cos\theta& 0& 0\\
0&0&1&0\\
0&0&0&1
\end{bmatrix}
\]
意思是\(z\)轴不动,\(x,y\)两个坐标按平面上的直接旋转。
y->z(绕x轴)
\[rotate_x(\theta)=
\begin{bmatrix}
1&0&0&0 \\
0& cos\theta& -sin\theta& 0\\
0& sin\theta& cos\theta& 0\\
0&0&0&1
\end{bmatrix}
\]
意思是\(x\)轴不动,\(y,z\)两个坐标按平面上的直接旋转。
x->z(绕y轴)
注意:仔细看上面那张坐标系的图,可以发现按照右手螺旋定则
\(z\times x=y\)
但是我们需要的是从\(x\)轴到\(z\)轴
所以我们从\(x\)轴转到\(z\)轴\(\theta\),实际上是从\(z\)轴转到\(x\)轴\(-\theta\)角,所以旋转矩阵写法稍微有一点变化
\[rotate_y(\theta)=
\begin{bmatrix}
cos\theta&0&sin\theta&0 \\
0&1&0&0 \\
-sin\theta&0&cos\theta&0\\
0&0&0&1
\end{bmatrix}
\]
绕任意轴的旋转
首先我们把这个轴旋转到\(x\)轴上(打个比方)
其次旋转角度直接分解成三根轴的角度,三个矩阵乘起来
最后再把这个轴转回去
听起来很简单是不是
这有个公式叫做\(\text{Rodrigues' rotation formula}\)
中文名:罗德里格斯旋转公式
\(V\)为待旋转向量,\(K\)为旋转轴(单位向量!所以不用考虑大小),\(\theta\)为旋转角,方向依右手螺旋定则
\[V_{rot}=Vcos\theta+(K\times V)sin\theta+K(K*V)(1-cos\theta)
\]
证明:

似乎都是从wiki上翻译的?不管了
所以首先对\(V\)分解为平行与\(K\)和垂直于\(K\)的两个分量
\[V_{\parallel}=K(K*V)
\]
\[V_{\bot}=-K\times(K\times V)
\]
这个可以看图理解
所以
\[V_{rot}=V_{\parallel}+V_{rot\bot} \\
V_{rot\bot}=cos\theta*V_{rot}+sin\theta*(K\times V_{\bot})\\
K\times V_{\bot}=K\times(V-V_{\parallel})=K\times V\]
所以把结果全部代回
\[V_{rot}=V_{\parallel}+cos\theta(V-V_{\parallel})+sin\theta(K\times V)
\]
整理得到上面那个公式
另外有一个矩阵形式
由于叉乘可以写成矩阵形式
对于\(K=[K_x,K_y,K_z]^{T}\),有叉积矩阵,用的时候直接左乘
\[\pmb{K}=\begin{bmatrix}
0&-K_z&K_y \\
K_z&0&-K_x \\
-K_y&K_x&0
\end{bmatrix}
\]
所以公式可以写成
\[\begin{aligned}
V_{rot}&=Vcos\theta+(K\times V)sin\theta+K(K*V)(1-cos\theta)\\
&=V-(1-cos\theta)(K*K)V+(1-cos\theta)(K*V)K+sin\theta \pmb{K}V\\
&=V+(1-cos\theta)[(K*V)K-(K*K)V]+sin\theta\pmb{K}V\\
&=V+(1-cos\theta)[K\times(K\times V)]+sin\theta\pmb{K}V\\
&=[\pmb{I}+(1-cos\theta)\pmb{K^2}+sin\theta \pmb{K}]V
\end{aligned}\]
第二行是因为\(K*K=1\)
第四行是向量三重积的性质
即
\[\pmb{R}=\pmb{I}+sin\theta\pmb{K}+(1-cos\theta)\pmb{K^2}\\
\pmb{V_{rot}}=\pmb{R}\pmb{V}\]






