[AGC005D]~K Perm Counting

题面：Luogu
题解：容斥
显然可以考虑设\(g[i]\)表示有至少\(i\)个位置符合\(|P[i]-i|=k\)

\[ans=\sum_{i=0}^{n}{(-1)^ig[i](n-i)!} \]

考虑怎么求出\(g[i]\)
考虑一个二分图，左边是位置，右边是该位置上的值，将冲突的边全部连起来

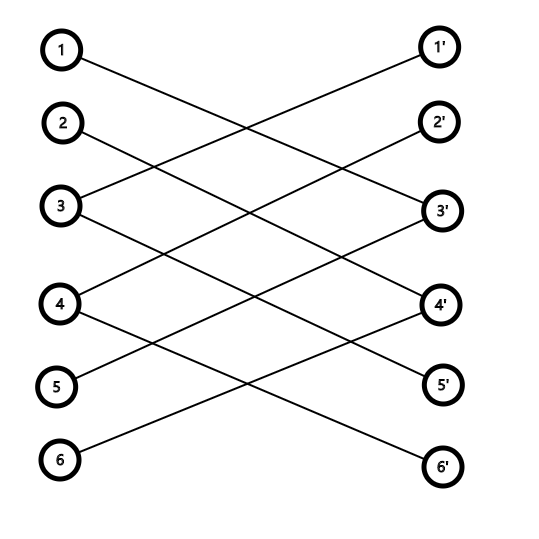
每一条链上，每个点只能连一条边
比如这个图是\(n=6,k=2\)
所以我们可以把链映射一下
对于这个图来说，也就是映射成\(1,3,5,1,3,5,2,4,6,2,4,6\)
然后直接对每一条链进行\(dp\)
设\(dp[i][j][0/1]\)表示递推第\(i\)个点，选了\(j\)条边，当前这条边选不选（就是和上一个点连不连）
判断是否是一条链上就是\(a[i]-a[i-1]==k\)
不选这条边的话很显然
\(dp[i][j][0]=dp[i-1][j][0]+dp[i-1][j][1]\)
选这条边也很显然（如果能选的话）
\(dp[i][j][1]=dp[i-1][j-1][0]\)
于是\(g[i]=dp[n*2][i][0]+dp[n*2][i][1]\)（选了一条边就代表一个位置上满足条件）

#include<bits/stdc++.h>
using namespace std;

inline void read(int& x)
{
	x = 0; char c = getchar();
	while (!isdigit(c)) c = getchar();
	while (isdigit(c)) x = x * 10 + c - '0', c = getchar();
}

#define P 924844033
#define maxn 2005
int dp[maxn << 1][maxn][2], fac[maxn];
int n, k, a[maxn << 1], cnt, ans;
inline int add(int x, int y) { return (0ll + x + y) % P; }
inline int dec(int x, int y) { return (0ll + x - y + P) % P; }
inline int mul(int x, int y) { return 1ll * x * y % P; }
int main()
{
	read(n), read(k);
	fac[0] = dp[1][0][0] = 1;
	for (int i = 1; i <= n; ++i) fac[i] = mul(i, fac[i - 1]);
	for (int i = 1; i <= k; ++i)
		for (int t = 0; t <= 1; ++t)
			for (int j = i; j <= n; j += k)
				a[++cnt] = j;
	for (int i = 2; i <= (n << 1); ++i)
		for (int j = 0; j <= (i >> 1); ++j)
		{
			dp[i][j][0] = add(dp[i - 1][j][0], dp[i - 1][j][1]);
			if (j && a[i] - a[i - 1] == k) dp[i][j][1] = dp[i - 1][j - 1][0];
		}
	for (int i = 0, tp; i <= n; ++i)
	{
		tp = add(dp[n << 1][i][0], dp[n << 1][i][1]);
		if (i & 1) ans = dec(ans, mul(tp, fac[n - i]));
		else ans = add(ans, mul(tp, fac[n - i]));
	}
	printf("%d\n", ans);
	return 0;
}