[NOI2011]阿狸的打字机

题意：Luogu
题解：AC自动机
对于fail树，我们有性质：如果有一条边\((u,v)\)，则\(u\)代表的字符串必然为\(v\)的后缀
对于trie树，我们有性质：如果有一条边\((u,v)\)，则\(u\)代表的字符串必然为\(v\)的前缀
还有一个性质：字串必定是某一后缀的一个前缀

---

询问是这样的：对于询问\((x,y)\)，求第\(x\)个打印的字符串在第\(y\)个打印的字符串中出现了多少次。
考虑对于每一组询问\((x,y)\)，我们可以先把询问离线，按y排序
我们还要预处理出每一个串的结束节点\(root\)和这个节点对应的编号\(id\)
按trie树建树的顺序dfs，每递归到一个点，如果这是一个结束节点，就处理掉这个点的所有询问

---

我们首先把fail树的dfs序求出来，设为\(dfs\_l\)和\(dfs\_r\)
在trie树上dfs时，先对这个点的\(dfs\_l[rt]\)的值+1
对于每个询问\(x\)，答案即为\(\big[dfs\_l[root[q[i].x]],dfs\_r[root[q[i].x]\big]\)的区间和
dfs回溯时再-1
所以上树状数组即可

---

问题来了，为什么可以这样？
下面是一个例子：插入的是hers his she i
这是连了fail指针的trie树（连向根节点的fail指针没放上去）

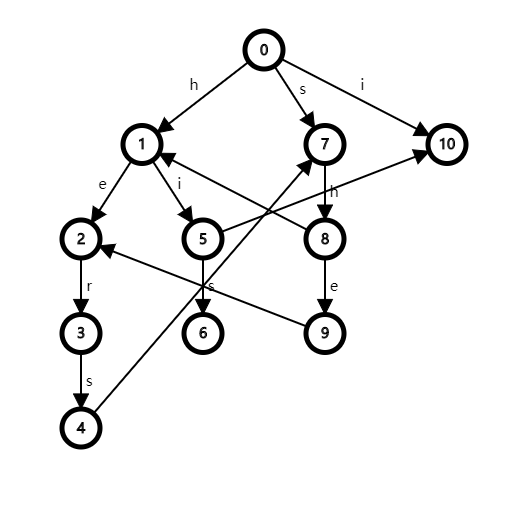
这是fail树

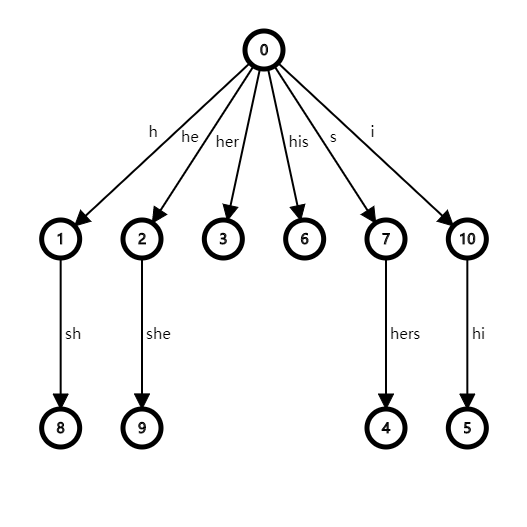
如果我们要查 i 在 his 中的出现次数
我们dfs到了6号节点，\(val[6]+=1\)
这是一个结束节点，所以我们开始处理询问
查询，查\([9,10]\)区间和（也就是10号节点的子树）
答案是1（因为此时trie树上4，5，6节点值都为1，对应在fail树上就是8，6，10节点为1）

---

统计区间保证了我们要找的模式串（i)是它子树中的所有串的后缀
trie树的dfs方式保证了我们统计的答案是所有原串（his）的前缀（h，hi，his）
两者的交就是所有原串的前缀的后缀是模式串的数量，也就是所求答案
最后上代码，大多数都封了namespace，应该能看懂吧

#include<bits/stdc++.h>
using namespace std;
inline void read(int& x)
{
	x = 0; char c = getchar();
	while (!isdigit(c)) c = getchar();
	while (isdigit(c)) x = x * 10 + c - '0', c = getchar();
}
#define maxn 100005
int root[maxn], id[maxn], ql[maxn], qr[maxn], ans[maxn];
struct Query
{
	int x, y, id, ans;
	bool operator < (const Query& p) const { return y < p.y; }
}q[maxn];
namespace Tree
{
	struct Edge
	{
		int fr, to;
	}eg[maxn << 1];
	int head[maxn], edgenum;
	inline void add(int fr, int to)
	{
		eg[++edgenum] = { head[fr],to };
		head[fr] = edgenum;
	}
	int dfn_clock, dfs_l[maxn], dfs_r[maxn];
	void dfs(int rt)
	{
		dfs_l[rt] = ++dfn_clock;
		for (int i = head[rt]; i; i = eg[i].fr) dfs(eg[i].to);
		dfs_r[rt] = dfn_clock;
	}
};
using namespace Tree;
namespace Bitarray
{
	int c[maxn];
	inline int lowbit(int& x) { return x & (-x); };
	inline void update(int& pos, int v) { for (int i = pos; i <= dfn_clock; i += lowbit(i)) c[i] += v; }
	inline int query(int pos) { int ans = 0; for (int i = pos; i; i -= lowbit(i)) ans += c[i]; return ans; }
}
using namespace Bitarray;
namespace AC_automaton
{
	int son[maxn][26], fail[maxn], fa[maxn], tot, Son[maxn][26];
	//有两个son是因为第一次会把原来的trie树补成图（也就是加了fail），然而第二次我们需要dfs的是树
	inline void getfail()//我把建fail树封到这里面了
	{
		queue<int> q;
		for (int i = 0; i < 26; ++i)
			if (son[0][i]) q.push(son[0][i]), add(0, son[0][i]);
		while (!q.empty())
		{
			int tp = q.front(); q.pop();
			for (int i = 0; i < 26; ++i)
			{
				if (son[tp][i])
				{
					fail[son[tp][i]] = son[fail[tp]][i];
					q.push(son[tp][i]);
					add(fail[son[tp][i]], son[tp][i]);
				}
				else son[tp][i] = son[fail[tp]][i];
			}
		}
	}
};
using namespace AC_automaton;
char s[maxn];
int cnt, Q;
void Dfs(int rt)//得到答案
{
	update(dfs_l[rt], 1);
	if (id[rt])
		for (int i = ql[id[rt]]; i <= qr[id[rt]]; ++i)
			q[i].ans = query(dfs_r[root[q[i].x]]) - query(dfs_l[root[q[i].x]] - 1);
	for (int i = 0; i < 26; ++i) if (Son[rt][i]) Dfs(son[rt][i]);
	update(dfs_l[rt], -1);
}
int main()
{
	scanf("%s", s);
	for (int i = 0, rt = 0; s[i]; ++i)
	{
		if (s[i] >= 'a' && s[i] <= 'z')
		{
			if (!son[rt][s[i] - 'a']) son[rt][s[i] - 'a'] = ++tot, fa[tot] = rt;
			rt = son[rt][s[i] - 'a'];
		}
		else if (s[i] == 'B') rt = fa[rt];
		else root[++cnt] = rt, id[rt] = cnt;
	}
	for (int i = 0; i <= tot; ++i)
		for (int j = 0; j < 26; ++j) Son[i][j] = son[i][j];
	getfail(); dfs(0);
	read(Q);
	for (int i = 1; i <= Q; ++i) read(q[i].x), read(q[i].y), q[i].id = i;
	sort(q + 1, q + Q + 1);
	for (int i = 1, pos = 1; i <= Q; i = pos)//合并询问
	{
		ql[q[i].y] = i;
		while (q[pos].y == q[i].y) ++pos;
		qr[q[i].y] = pos - 1;
	}
	Dfs(0);
	for (int i = 1; i <= Q; ++i) ans[q[i].id] = q[i].ans;
	for (int i = 1; i <= Q; ++i) printf("%d\n", ans[i]);
	return 0;
}