[POI2011]Lightning Conductor

JSOI2016灯塔跟这个一模一样（数据范围还比原题小）
题面：Luogu
60分题解：st表（也就是我上面说的那道题）
我们要对每个i求出

\[\max\left\{a_j+\left\lceil\sqrt{|i-j|}\right\rceil\right\}-a_i \]

\(\sqrt{|i-j|}\)只有\(\sqrt n\)种，直接枚举，用st表求出最大值
复杂度:\(O(n\sqrt n)\)

#include<bits/stdc++.h>
using namespace std;
inline void read(int& x)
{
	x = 0; char c = getchar();
	while (!isdigit(c)) c = getchar();
	while (isdigit(c)) x = x * 10 + c - '0', c = getchar();
}
#define maxn 500005
int lg[maxn], st[maxn][21], h[maxn], n;
inline int getans(int l, int r)
{
	int tp = lg[r - l + 1];
	return max(st[l][tp], st[r - (1 << tp) + 1][tp]);
}
inline void st_init()
{
	for (int i = 2; i <= n; ++i) lg[i] = lg[i >> 1] + 1;
	for (int i = 1; i <= n; ++i) st[i][0] = h[i];
	for (int i = 1; i <= 19; ++i)
		for (int j = 1; j + (1 << i) - 1 <= n; ++j)
			st[j][i] = max(st[j][i - 1], st[j + (1 << (i - 1))][i - 1]);
}
int main()
{
	read(n);
	for (int i = 1; i <= n; ++i) read(h[i]);
	st_init();
	for (int i = 1; i <= n; ++i)
	{
		int ans = 0;
		for (int j = 1;; ++j)
		{
			int l = (j - 1) * (j - 1) + 1, r = j * j;
			if (i + l <= n) ans = max(ans, getans(i + l, min(n, i + r)) + j - h[i]);
			if (i - l >= 1) ans = max(ans, getans(max(1, i - r), i - l) + j - h[i]);
			if (i - r <= 1 && i + r >= n) break;
		}
		printf("%d\n", ans);
	}
	return 0;
}

---

还有一种用决策单调性+分治/单调队列的，复杂度\(O(n\log n)\)
首先是单调队列
单调队列维护形如\(\sqrt{x-a}+b\)的一系列图像
转移时二分出两条曲线相交的点

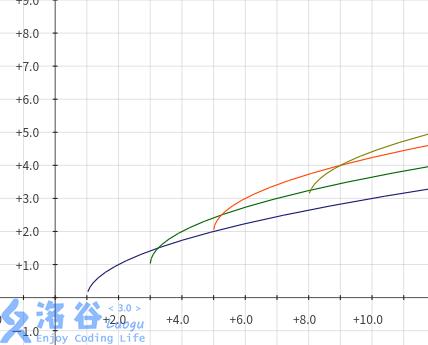
然后反过来再做一遍
因为上面的转移方程是

\[\max_{j=1}^{i}\left\{a_j+\left\lceil\sqrt{i-j}\right\rceil\right\}-a_i \]

#include<bits/stdc++.h>
using namespace std;

inline void read(int& x)
{
	x = 0; char c = getchar();
	while (!isdigit(c)) c = getchar();
	while (isdigit(c)) x = x * 10 + c - '0', c = getchar();
}
#define maxn 500005
double sq[maxn];
int n, a[maxn], p[maxn], maxp[maxn];
struct Node
{
	int a, b;
	inline friend double calc(Node x, int X) { return sq[X - x.a] + x.b; }
	inline friend int get(Node X, Node Y)
	{
		int l = Y.a, r = n + 1, mid;
		while (l < r)
		{
			mid = (l + r) >> 1;
			if (calc(Y, mid) >= calc(X, mid)) r = mid;
			else l = mid + 1;
		}
		return l;
	}
};
template<typename T>
struct Deque
{
	int head, tail;
	T val[maxn];
	void clear() { head = 1, tail = 0; }
	T back() { return val[tail]; }
	T front() { return val[head]; }
	void pop_back() { --tail; }
	void pop_front() { ++head; }
	void push_back(T v) { val[++tail] = v; }
	void push_front(T v) { val[++head] = v; }
	bool empty() { return head > tail; }
};
Deque<Node> q;
Deque<int> Q;
void work()
{
	q.clear(); Q.clear();
	Node tp;
	for (int i = 1; i <= n; ++i)
	{
		tp = { i,a[i] };
		while (!q.empty() && get(q.back(), tp) <= Q.back()) q.pop_back(), Q.pop_back();
		Q.push_back(!q.empty() ? get(q.back(), tp) : 1);
		q.push_back(tp);
		while (Q.head < Q.tail && i >= Q.val[Q.head + 1]) ++Q.head, ++q.head;
		maxp[i] = max(maxp[i], (int)ceil(calc(q.front(), i)) - a[i]);
	}
}
int main()
{
	read(n);
	for (int i = 1; i <= n; ++i) read(a[i]), sq[i] = sqrt(i);
	work();
	reverse(a + 1, a + n + 1), reverse(maxp + 1, maxp + n + 1);
	work();
	for (int i = n; i; --i) printf("%d\n", maxp[i]);
	return 0;
}

---

分治
设\(p[l]\sim p[r]\)的最优决策点在\([L,R]\)间
设\(mid=\frac{l+r}{2}\)，扫一遍扫出来\(mid\)的最优决策点
然后就可以分治了（由决策单调性，\(p[l]\sim p[mid-1]\)d的最优决策点在\([L,pos]\)间）
分治又好写又跑得快，真香（总时间分治0.77s,单调队列2.41s(也可能是我单调队列写丑了，因为最优解也是单调队列）

#include<bits/stdc++.h>
using namespace std;

inline void read(int& x)
{
	x = 0; char c = getchar();
	while (!isdigit(c)) c = getchar();
	while (isdigit(c)) x = x * 10 + c - '0', c = getchar();
}
#define maxn 500005
double sq[maxn], p[maxn];
int n, a[maxn];
void solve(int l, int r, int L, int R)
{
	if (l > r) return;
	int mid = (l + r) >> 1, pos = mid;
	double tmp, tmp_p;
	tmp_p = a[mid];
	for (int i = L; i <= min(R, mid); ++i)
	{
		tmp = a[i] + sq[mid - i];
		if (tmp > tmp_p) tmp_p = tmp, pos = i;
	}
	p[mid] = max(p[mid], tmp_p - a[mid]);
	solve(l, mid - 1, L, pos), solve(mid + 1, r, pos, R);
}

int main()
{
	read(n);
	for (int i = 1; i <= n; ++i) read(a[i]), sq[i] = sqrt(i);
	solve(1, n, 1, n);
	reverse(a + 1, a + n + 1), reverse(p + 1, p + n + 1);
	solve(1, n, 1, n);
	for (int i = n; i; --i) printf("%d\n", (int)ceil(p[i]));
	return 0;
}