基础线段树

线段树是一颗二叉树，支持区修区查，而且适用范围比较广泛 (不过常数略大)

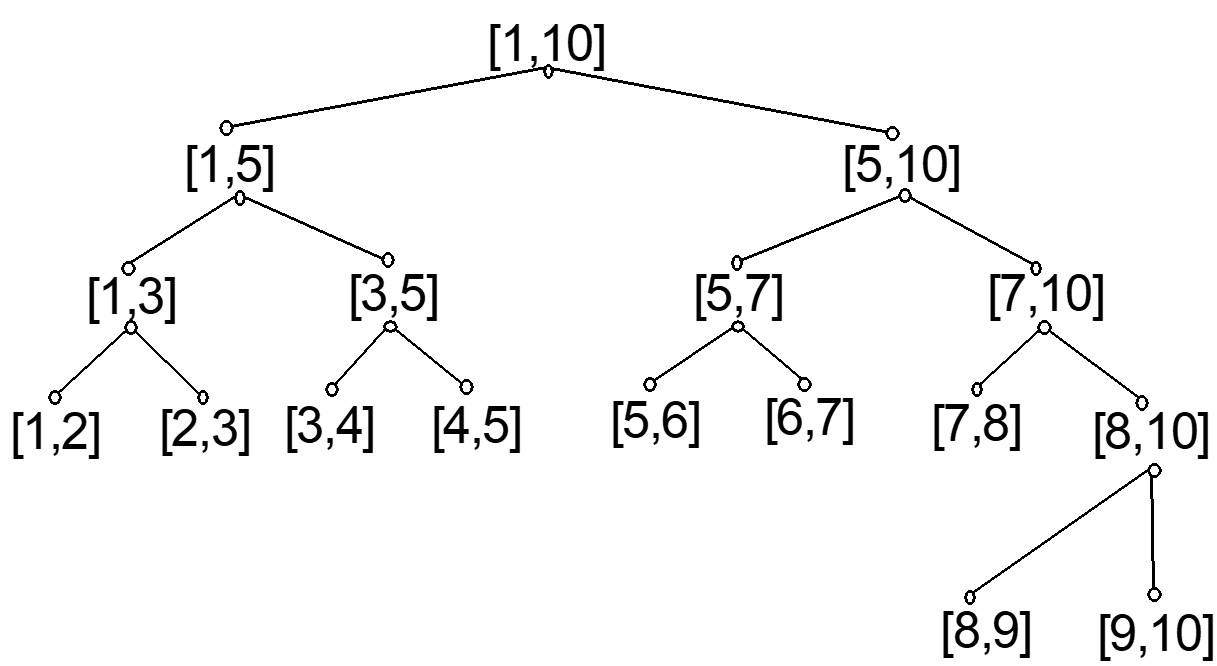
码风：结构体数组实现
首先建树，数组要开到最大数据的4倍
给个证明吧 (虽然挺简单的)
证明

---

以单点修改，区间查询求区间和为例
首先是上传和建树操作

struct Node
{
    int l,r,v;//可以加一堆数据上去
}node[MAX<<2];
#define lson rt<<1,l,mid
#define rson rt<<1|1,mid+1,r
void pushup(int rt)//更新父节点数据
{
    node[rt].v=node[rt<<1].v+node[rt<<1|1].v;
}
void construct(int rt,int l,int r)
{
    node[rt].l=l;
    node[rt].r=r;
    if(l==r)
        node[rt].v=a[l];//叶子节点,a数组是初始值
    construct(lson);
    construct(rson);
    pushup(rt);
}

其次是线段树的精髓：修改和查询。其实这两个非常像(直接CTRL+C再改一下就好了)

void modify(int rt,int l,int r,int fr,int to,int v)//l,r为当前节点的左右(也可以直接写成node[rt].l和.r省掉两个参数)。fr,to是要修改的区间
{
    if(fr<=l&&to>=r)//全部包含就直接修改
    {
        node[rt].v+=(r-l+1)*v；
        return;
    }
    int mid=(l+r)>>1;
    if(fr<=mid) modify(lson,fr,to,v);//修改左儿子
    if(to>mid) modify(rson,fr,to,v);//修改右儿子,注意这个原本是to>=mid+1，可以直接写成>mid
    pushup(rt);//不能漏了
}
int query(int rt,int l,int r,int fr,int to,int v)//fr,to是要查询的区间
{
    if(fr<=l&&to>=r)//全部包含就直接返回
        return node[rt].v;
    int mid=(l+r)>>1,ans=0;
    if(fr<=mid) ans+=query(lson,fr,to,v);//查询左儿子
    if(to>mid) ans+=query(rson,fr,to,v);//查询右儿子
    return ans;
}

---

接下来是区修区查
我们需要用到一个lazy标记
比方说我要更新一段区间，如果全部覆盖了node[rt]这一段区间我就不继续往下修改
而是在这个节点这里打一个lazy标记(延迟标记)
大概意思就是父节点欠了子节点多少，先不还，等查询时再还 (手动滑稽)
这样就可以让线段树维持在\(O(n\log n)\)的复杂度(否则会退化到\(O(n^{2})\))
代码修改的话我们需要加一个下传函数,结构体里面再定义一个lazy初始化为0

void pushdown(int rt)
{
    if(node[rt].lazy)
    {
        node[rt<<1].v+=(node[rt<<1].r-node[rt<<1].l+1)*node[rt].lazy;
        node[rt<<1|1].v+=(node[rt<<1|1].r-node[rt<<1|1].l+1)*node[rt].lazy;
        node[rt<<1].lazy+=node[rt].lazy;
        node[rt<<1|1].lazy+=node[rt].lazy;
        node[rt].lazy=0;
    }
}

同时modify和query需要一点小修改
modify函数：

void modify(int rt,int l,int r,int fr,int to,int v)
{
    if(fr<=l&&to>=r)
    {
        node[rt].lazy+=v;//更新lazy标记
        node[rt].v+=(r-l+1)*v；
        return;
    }
    int mid=(l+r)>>1;
    pushdown(rt);//修改子节点前先下传
    if(fr<=mid) modify(lson,fr,to,v);
    if(to>mid) modify(rson,fr,to,v);
    pushup(rt);//不能漏了
}

query函数：

int query(int rt,int l,int r,int fr,int to,int v)
{
    if(fr<=l&&to>=r)
        return node[rt].v;
    int mid=(l+r)>>1,ans=0;
    pushdown(rt);//查询子节点前先下传
    if(fr<=mid) ans+=query(lson,fr,to,v);
    if(to>mid) ans+=query(rson,fr,to,v);
    return ans;
}

来一个模板题洛谷P3372