树状数组简介

简单讲一下我对树状数组的理解

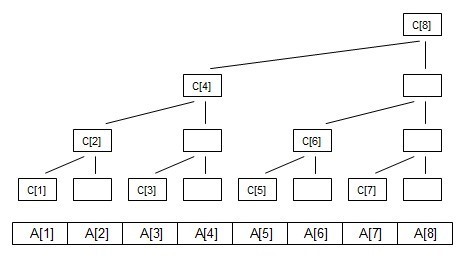
c[i]等于它所管辖区域的a的和(或者其他的)
这就是树状数组的原理
树状数组的优势在于代码好写且常数较小
缺点是适用范围较小，只适用于可以从\([1,r]\)和\([1,l]\)推出\([l,r]\)的问题
最常用的就是维护区间和

---

以下代码以求前缀和(单点修改，区间查询)为例,数组下标从1开始,a[i]为初始数组，c[i]为树状数组
1.最基本的\(O(1)lowbit\)
这可以得到当前数字二进制表示下的最后一个1是代表的多大的数
例如\(25_{(2)}=11001 \quad lowbit(25)=1\),\(24_{(2)}=1100 \quad lowbit(24)=8\)

int lowbit(int x)
{
    return x&(-x);//eg:25=11001,-25=00110(按位取反)+1=00111,25&(-25)=1(与运算就是两个二进制数按位比较，都为1则为1）
}

2.\(O(\log{n})\)修改

void modify(int place,int val)
{
    for(int i=place;i<=n;i+=lowbit(i))//i+=lowbit(i)可以这么理解:把最后一个1的位置加一个1并进位,如6会变成8,5会变成6等,对照上面的图相当于往上走一级
            c[i]+=val;
}

3.\(O(\log{n})\)查询

int getsum(int x)//求[1,x]的和
{
    int ans=0;
    for(int i=x;i;i-=lowbit(i))//比如求[1,6]的和，就相当于先加上[5,6](c[6]),再加上[1,4](c[4])
        ans+=c[i];
    return ans;
}

求\([l,r]\)的和就相当于先求出\([1,r]\)的和再减去\([1,l-1]\)的和
是不是板子极其好背啊

---

再就是区间修改
利用差分
设差分数组为\(d[i]=a[i]-a[i-1] \quad d[1]=a[1]\)
则

\[\begin{split} \sum_{i=1}^{x} a[i] & =\sum_{i=1}^{x} \sum_{j=1}^{i}d[j] \newline & =\sum_{i=1}^{x}(x-i+1)* d[i] \newline & =(x+1)* \sum_{i=1}^{x}d[i]-\sum_{i=1}^{x}i* d[i] \newline \end{split} \]

所以我们只要维护两个树状数组c[i]为a[i]的前缀和，c2[i]为\(i*a[i]\)所产生的新数列的前缀和
代码只需在初始化时\(\text modify(i,a[i]-a[i-1])\),查询时再设一个\(\text ans2+=i*c2[i]\)并\(\text return (x+1)*ans-ans2\)
注意在修改\([l,r]\)时是在l修改+val,r+1是修改-val(因为这是一个差分数组）
两道模板题LuoguP3374 LuoguP3368
一般这种题都要开long long
贴两个代码

// 单修区查,P3374
#include<bits/stdc++.h>
using namespace std;
#define N 500005
long long a[N],c[N];
int n,m,y,z,op;
int lowbit(int i)
{
    return i&(-i);
}
void modify(int place,int value)
{
    for(int i=place;i<=n;i+=lowbit(i))
        c[i]+=value;
}
int getsum(int place)
{
    int ans=0;
    for(int i=place;i;i-=lowbit(i))
        ans+=c[i];
    return ans;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
    	scanf("%d",&op);
    	modify(i,op);
    }
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&op,&y,&z);
        if(op==1)
            modify(y,z);
        else
            printf("%d\n",getsum(z)-getsum(y-1));
    }
    return 0;
}

// 区修单查(和上一道题结合就是区修区查),P3368
#include<bits/stdc++.h>
using namespace std;
#define N 500005
long long a[N],c[N],c2[N];
int n,m,x,y,z,op;
int lowbit(int i)
{
    return i&(-i);
}
void modify(int place,int value)
{
    for(int i=place;i<=n;i+=lowbit(i))
        c[i]+=value,c2[i]+=place*value;
}
int getsum(int place)
{
    int ans1=0,ans2=0;
    for(int i=place;i;i-=lowbit(i))
        ans1+=c[i],ans2+=c2[i];
    return (place+1)*ans1-ans2;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
    	scanf("%lld",&a[i]);
    	modify(i,a[i]-a[i-1]);
    }
    for(int i=1;i<=m;i++)
    {
        scanf("%d",&op);
        if(op==1)
            scanf("%d%d%d",&y,&z,&x),modify(y,x),modify(z+1,-x);
        else
            scanf("%d",&x),printf("%d\n",getsum(x)-getsum(x-1));
    }
    return 0;
}