JAVA程序设计-有理数类的设计
1.有理数类代码
package rationalNumber;
public class Rational {// 类中含有方法
private int numerator; // 分子
private int denominator; // 分母
public int getNumerator() { // 获取分子
return numerator;
}
public int getDenominator() { // 获取分母
return denominator;
}
public Rational() { // 构造方法
this.numerator = 0;
this.denominator = 1;
}
public Rational(int x) { // 传入参数为整数时,构造有理数
if (x < 0) {
this.numerator = -x; // 分子为正数
this.denominator = -1;
} else {
this.numerator = x;
this.denominator = 1;
}
}
public Rational(int numerator, int denominator) { // 参数为两整数,以分数形式构造有理数
if (denominator == 0) {
System.out.println("错误,分母不能为零!");
System.exit(0);
} else if (numerator == 0) {
this.numerator = 0;
this.denominator = denominator;
return;
}
int numMax = getNumMax(numerator, denominator);// numMax为分子分母的最大公约数
this.numerator = numerator / numMax;
this.denominator = denominator / numMax;
}
public Rational(Double x) { // 参数含有小数点时构造有理数
int flag = 0;
if (x < 0) {
flag = 1;
x = -x;
}
String str = x.toString(); // 把小数分割成两部分
String[] st = new String[2];
st = str.split("\\.");
int numOne = (int) (Integer.parseInt(st[0]) * Math.pow(10, st[1].length()) + Integer.parseInt(st[1])); // 小数化为分数时的分子
int numTwo = (int) Math.pow(10, st[1].length()); // 小数化为分数时的分母
int numMax = getNumMax(numOne, numTwo);
this.numerator = numOne / numMax;
if (flag == 1) { // 小数为负数
this.denominator = (-1) * numTwo / numMax;
} else {
this.denominator = numTwo / numMax;
}
}
private int getNumMax(int a, int b) { // 获取最大公约数
int temp;
temp = a % b;
while (temp != 0) {
a = b;
b = temp;
temp = a % b;
}
return b;
}
public Rational add(Rational anOther) { // 相加运算
int numOne = anOther.numerator * this.denominator + anOther.denominator * this.numerator; // 相加所得分数的分子
int numTwo = anOther.denominator * this.denominator; // 相加所得分数的分母
Rational result = new Rational(numOne, numTwo);
return result;
}
public Rational minus(Rational anOther) { // 相减运算
int numOne = this.numerator * anOther.denominator - this.denominator * anOther.numerator; // 相减所得分数的分子
int numTwo = anOther.denominator * this.denominator; // 相减所得分数的分母
Rational result = new Rational(numOne, numTwo);
return result;
}
public Rational multiply(Rational anOther) { // 相乘运算
int numOne = anOther.numerator * this.numerator; // 相乘所得分数的分子
int numTwo = anOther.denominator * this.denominator; // 相乘所得分数的分母
Rational result = new Rational(numOne, numTwo);
return result;
}
public Rational divide(Rational anOther) { // 相除运算
int numOne = this.numerator * anOther.denominator; // 相除所得分数的分子
int numTwo = this.denominator * anOther.numerator; // 相除所得分数的分母
Rational result = new Rational(numOne, numTwo);
return result;
}
public Rational abs() { // 取绝对值
int numOne, numTwo;
if (this.numerator < 0) {
numOne = -this.numerator;
} else {
numOne = this.numerator;
}
if (this.denominator < 0) {
numTwo = -this.denominator;
} else {
numTwo = this.denominator;
}
Rational result = new Rational(numOne, numTwo);
return result;
}
public Rational getPow(Rational number, int n) { // 获取有理数number的n次方
int numOne = number.numerator;
int numTwo = number.denominator;
for (int i = 1; i < n; i++) {
numOne = numOne * number.numerator;
numTwo = numTwo * number.denominator;
}
Rational result = new Rational(numOne, numTwo);
return result;
}
public Rational remain(Rational number) { // 取余
if (this.divide(number).denominator == 1) { // 能够整除
Rational result = new Rational(0, 1);
return result;
}
Rational result;
if (this.divide(number).denominator == this.denominator * number.numerator) {
result = new Rational(this.numerator * number.denominator, 1);
} else {
result = new Rational(this.numerator, 1);
}
return result;
}
public void compare(Rational number) { // 比较大小
if (number.judgeSign().equals("此有理数是正数") && this.judgeSign().equals("此有理数是负数")) {
System.out.println(number.toString() + "更大");
} else if (number.judgeSign().equals("此有理数是负数") && this.judgeSign().equals("此有理数是正数")) {
System.out.println(this.toString() + "更大");
} else { // 两个有理数同号
if (number.toDouble() == this.toDouble()) {
System.out.println("两个有理数大小相等");
} else if (number.toDouble() > this.toDouble()) {
System.out.println(number.toString() + "更大");
} else if (number.toDouble() < this.toDouble()) {
System.out.println(this.toString() + "更大");
}
}
}
public String judgeSign() { // 判断有理数的正负性
String str = "";
if (this.numerator == 0) {
str = "此有理数为0";
}
if ((this.numerator < 0 && this.denominator < 0) || (this.numerator > 0 && this.denominator > 0)) {
str = "此有理数是正数";
} else if (this.denominator < 0 || this.numerator < 0) {
str = "此有理数是负数";
}
return str;
}
public int toInt() { // 有理数转化为int类型
return (int) this.numerator / this.denominator;
}
public double toDouble() { // 有理数转化为double类型
return (double) this.numerator / this.denominator;
}
public String toString() // 转化为字符串
{
Rational num = new Rational(0, 1);
String str = new String();
num.numerator = this.numerator;
num.denominator = this.denominator;
if (num.numerator * num.denominator < 0) { // 有理数为负数
str = str + "-";
}
num = abs();
if (num.denominator == 1) {
str = str + num.numerator;
} else {
str = str + num.numerator + "/" + num.denominator;
}
return str;
}
}
2.实现及测试代码
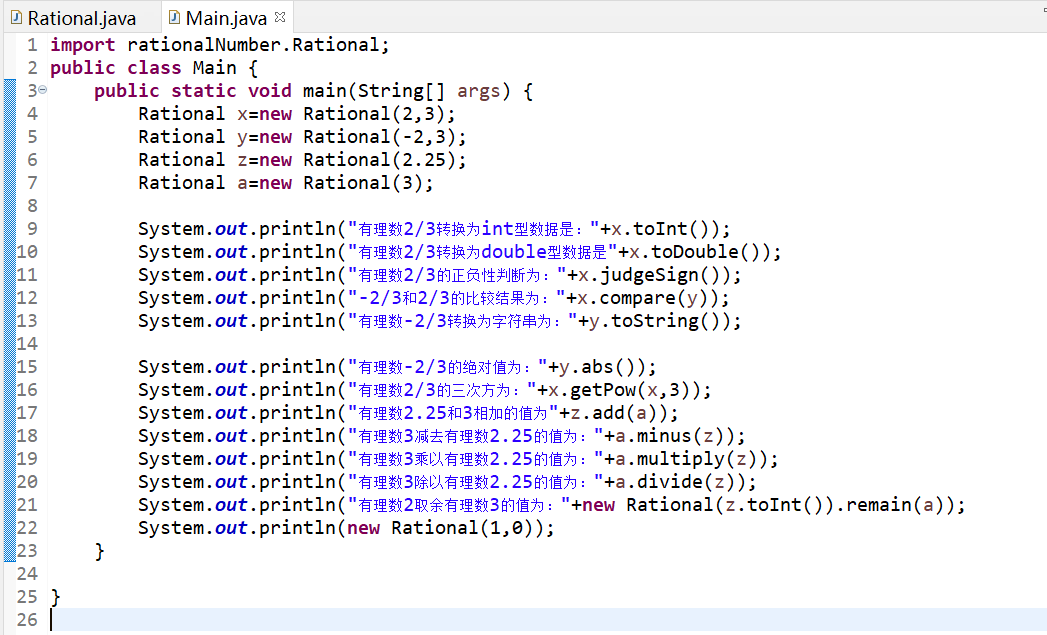
2.1 结果如下:
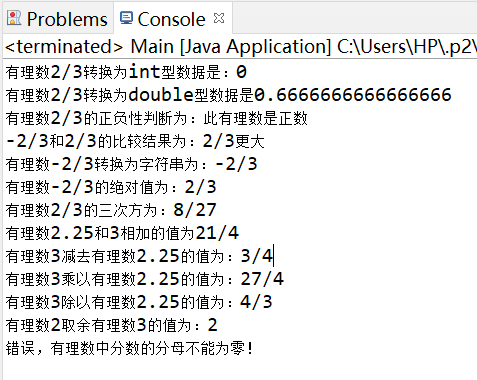
3. 尝试描述怎么与c语言的有理数代码相比较,为什么你设计的类更加面向对象?
- 新建一个对象(类的实例)时,此对象具有相应的属性,可以调用设计的类中的方法。而C语言中的有理数代码会更注重于函数的设计,更注重于编译过程中对于每个函数模块的调用,而不是面向对象的属性和方法进行相应的处理。
4. 尝试从代码复用的角度来描述你设计的有理数类。从几个方面讨论。
4.1 别人如何复用你的代码?
- 只需要在程序开头加上语句"import rationalNumber.Rational;",通过import关键字导入包rationalNumber中的类Rational。
4.2 别人的代码是否依赖你的有理数类的属性?当你的有理数类的属性修改时,是否会影响他人调用你有理数类的代码?
- 会依赖有理数类的属性;会影响他人调用有理数类的代码,比如类中构造时,参数若改变,那么就要输入不同的参数。
4.3 有理数类的public方法是否设置合适?为什么有的方法设置为private?
- 合适,这样不同包中的其他类也可以调用有理数类;因为他人无需访问此方法,比如求最大公约数的方法getNumMax,他人调用有理数类时,创建对象时,无需访问此方法,只需要了解构造方法就行。






