最小生成树
最小生成树
就是在一个 n 个点的连通图里
取 n-1 条边
使 n 个点 连通
并且 这 n-1 条边 的和 最小
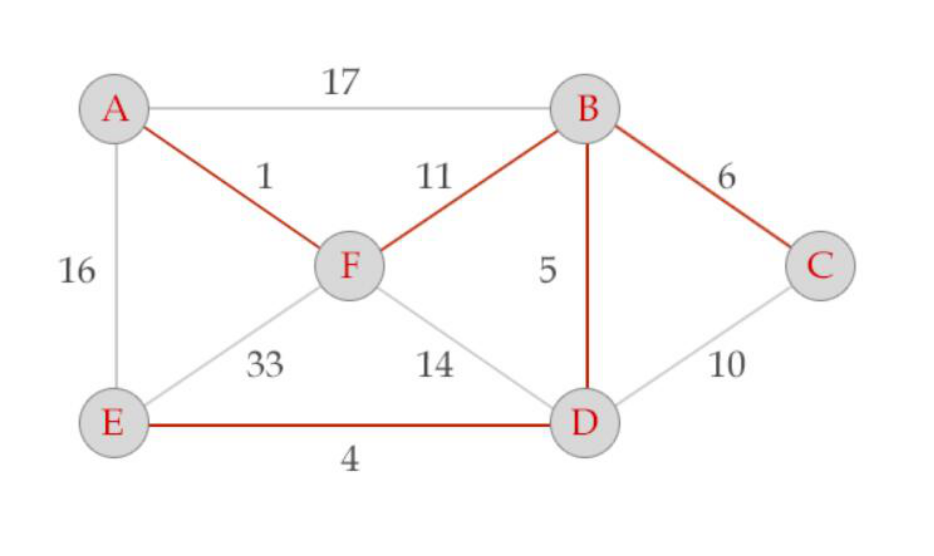
如 红边 是 最小生成树
最小生成树 主要就是通过 下面的两种方法
Prim算法 和 Kruskal算法 来解决
然后 这两种算法 采用的思路 不同
但是 到达同样的 结果
具体选择
可以根据题目的 特点 或者 个人喜好
我个人觉得 K算法 写起来很爽
但理性地讲
P算法 的复杂度 主要取决于 节点数
K算法 的复杂度 主要取决于 边数
所以 当点一样多时 比较稀疏(边少)的图 用 K算法
比较稠密(边多)的图 用 P算法
Kruskal算法
两步就能解决的
相当容易理解的
个人情有独钟的
K算法
两步
既然最小生成树 一定要取 n-1 条边
那么 取边的时候 就 能小则小 喽
所以 第一步
将所有的边 按边权 从小到大排序
过
第二步
选边的时候 很明显地 “ 选前 n-1 条边” 是错的
所以 从小到大 能选则选 直到选了 n-1 条为止
第二步过 简单的要死
注释
所谓 “能选则选” :
因为 最小生成树 是树 是没有环的
所以 选边的时候也不能出现 环
每次成功 选出一条边 就把 边连接的两个连通块 合并
所谓 “ 成功 选出 ”:
该边的 两个端点 不在同一连通块里
如果在同一个连通块里 就成环了
代码

#include <bits/stdc++.h> using namespace std; const int maxn=100000+15; const int maxm=100000+15; struct Edge { int x,y,z; }edge[maxm]; int n,m,tot; // 由小到大 bool cmp(Edge a,Edge b) { return a.z<b.z; } int top[maxn]; // 判断连通块 的 时候 用到了 并查集 int found(int x) { if (top[x]==x) return x; return top[x]=found(top[x]); } int main() { scanf("%d%d",&n,&m); tot=n-1;// 需要 取 tot 条边 for (int i=1;i<=m;i++) { scanf("%d%d%d",&edge[i].x,&edge[i].y,&edge[i].z); } sort(edge+1,edge+m+1,cmp); // 第一步 排序 for (int i=1;i<=n;i++) top[i]=i; // 初始化 连通块 int ans=0; for (int i=1;tot;i++) { int fx=found(edge[i].x),fy=found(edge[i].y); // 可以 把 fx 理解为 x 所在 连通块 编号 fy 同理 if (fx!=fy) { tot--; // 计数器 -1 ans+=edge[i].z; //累加 答案 top[fx]=fy; //连通块合并 } } printf("%d\n",ans); return 0; }
Prim算法
先选取一个 蓝点
然后不断 把白点 加入蓝点 的一个过程
1 初始化 V’={x} E’={} V'是蓝点
x是随便一个节点
2 重复下列操作 直到V’=V
在E集合当中 选择最小的边 <u,v>
使得 u∈V’ 但是 v∉V’ u是蓝点 v是白点
V’ 中加入节点 v E’ 中加入<u,v>
3 (V’,E’)则为所求的最小生成树。
分析
1 中 的 x 随便 一个点 即可
2 一直 选最小的 连接 V' 与 !V’ 的 边
这一步可用 heap 堆 (优先队列) 优化
维护一个 u∈V’ 但是 v∉V’ 的边集
就能 迅速取出 满足要求 的边
代码

#include <bits/stdc++.h> using namespace std; const int maxn=100000+15; const int maxm=100000+15; struct Edge { int x,y,z,next; Edge(int x=0,int y=0,int z=0,int next=0):x(x),y(y),z(z),next(next) {} }edge[maxm*2]; const bool operator < (const Edge &a,const Edge &b)//定义 小根堆 { return a.z>b.z; } int n,m; int sumedge,head[maxn]; int ins(int x,int y,int z) { edge[++sumedge]=Edge(x,y,z,head[x]); return head[x]=sumedge; } priority_queue <Edge> que; int ans; bool boo[maxn]; int main() { scanf("%d%d",&n,&m); for (int i=1;i<=m;i++) { int x,y,z; scanf("%d%d%d",&x,&y,&z); ins(x,y,z); ins(y,x,z); } memset(boo,false,sizeof(boo)); // 初始 全为 白点 boo[1]=true; // 1 置为蓝点 for (int u=head[1];u;u=edge[u].next) que.push(edge[u]);// 堆中加边 for (int i=1;i<n;i++) //总共要取出 n-1 条边 { Edge temp; temp=que.top(); // 找到 满足 v 是 白点 for (;boo[temp.y];que.pop(),temp=que.top()); que.pop(); ans+=temp.z; boo[temp.y]=true;// 变蓝 for (int u=head[temp.y];u;u=edge[u].next) if (!boo[edge[u].y]) que.push(edge[u]);// 继续加 } printf("%d\n",ans); return 0; }




