计算编辑距离

编辑距离，又称Levenshtein距离，是指两个字串之间，由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。

例如将kitten一字转成sitting：

1. sitten （k→s）
2. sittin （e→i）
3. sitting （→g）

 

问题：找出字符串的编辑距离，即把一个字符串s1最少经过多少步操作变成编程字符串s2，操作有三种，添加一个字符，删除一个字符，修改一个字符

 

解析：

首先定义这样一个函数——edit(i, j)，它表示第一个字符串的长度为i的子串到第二个字符串的长度为j的子串的编辑距离。

显然可以有如下动态规划公式：

• if i == 0 且 j == 0，edit(i, j) = 0
• if i == 0 且 j > 0，edit(i, j) = j
• if i > 0 且j == 0，edit(i, j) = i
• if i ≥ 1  且 j ≥ 1 ，edit(i, j) == min{ edit(i-1, j) + 1, edit(i, j-1) + 1, edit(i-1, j-1) + f(i, j) }，当第一个字符串的第i个字符不等于第二个字符串的第j个字符时，f(i, j) = 1；否则，f(i, j) = 0。

参考代码：

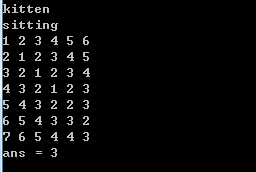
#include <math.h>
#include <stdio.h>
#include <string.h>
#include <iostream>
using namespace std;

#define N 50

void EditDistance(char *ch1, char *ch2)
{
    int len1 = strlen(ch1);
    int len2 = strlen(ch2);
    int **p = new int*[len2 + 1];                    // 二维数组空间动态分配
    for(int i = 0; i < len2+1; i++)
        p[i] = new int[len1 + 1];

    for(int i = 0; i < len2+1; i++)
        p[i][0] = i;
    for(int j = 1; j < len1+1; j++)
        p[0][j] = j;

    int flag;                                        // 记录ch2第i个数和ch1第i个数是否相等
    for(int i = 1; i < len2+1; i++)
    {
        for(int j = 1; j < len1+1; j++)
        {
            flag = (ch2[i-1]==ch1[j-1]) ? 0 : 1;     // 注意下标错位影响
            p[i][j] = min(min(p[i-1][j]+1, p[i][j-1]+1), p[i-1][j-1]+flag);
            printf("%d ", p[i][j]);
        }
        printf("\n");
    }
    printf("ans = %d\n", p[len2][len1]);

    for(int i = 0; i < len2+1; i++)                  /* 二维数组空间动态释放先内层后外层 */
    {
        delete p[i];
        p[i] = NULL;                                 // 避免野指针
    }
    delete [] p;
    p = NULL;                                        // 避免野指针
}

int main()
{
    char ch1[N], ch2[N];
    scanf("%s", ch1);
    scanf("%s", ch2);
    EditDistance(ch1, ch2);
    return 0;
}