SM3算法流程
注意：采用draw.io画的配图，插到博客园这里打开后真的好大，对不起各位看官。 ○|￣|_
1. SM3简介
SM3算法也是一种哈希算法，中国国家密码管理局在2010年发布，其名称是SM3密码杂凑算法，密码管理局有该算法的详细说明，可以到其网站下载《GBT 32905-2016 信息安全技术 SM3密码杂凑算法》和《GMT 0004-2012 SM3密码杂凑算法》。
-
算法的本质给任意长度的数据(\(l\le 2^{64}\))经过填充、迭代压缩后，生成固定长度的杂凑值,这个固定长度就是256比特。
-
处理过程：
- 第一步：填充。使填充后的数据的长度是512的整数倍。在数据的末尾上加一个1；然后把原始数据的长度用64比特表示，放在最后面；再看看现在的数据的长度值离512的整数还差多少个，差多少个就填多少个0在加的这个1和64比特的长度之间。
- 第二步：分组。把填充后的信息按照512比特一个分组进行分组。如果分成了n组，就是\(B^0,B^1,\dots,B^{n-1}\)个分组。
- 第三步：迭代压缩。对每一个分组都进行消息扩展，再借助寄存器得到最后的杂凑值（哈希值）。迭代压缩这里有很多中间变量和寄存器的操作，具体还是看一下算法。
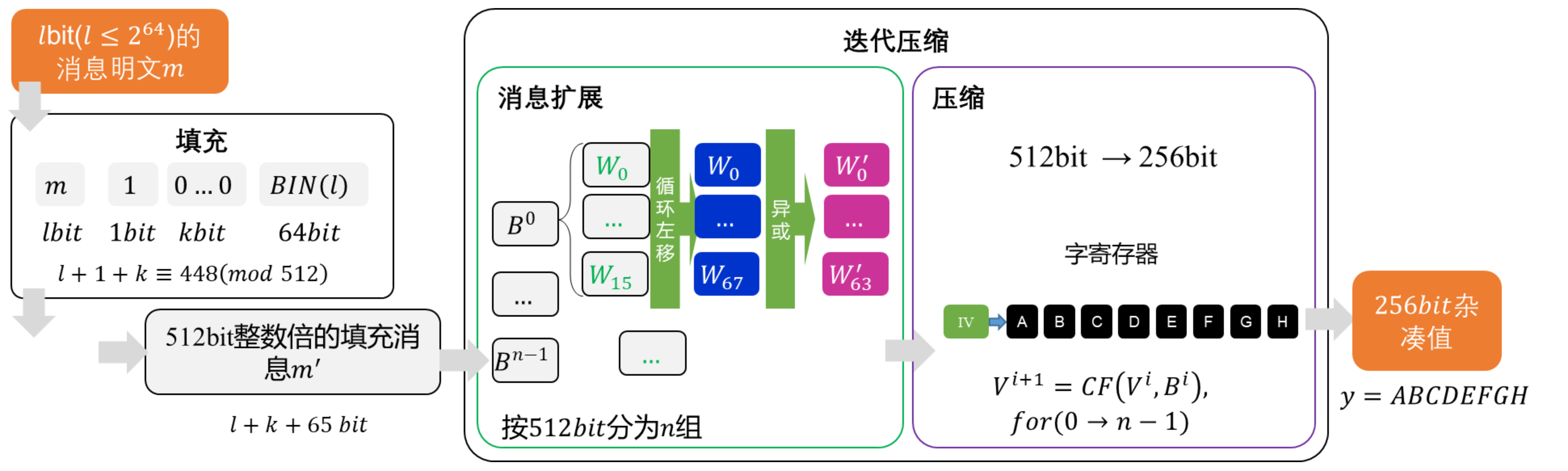
分组的目的是为了把填充后的消息\(m^{'}\)能拆成512比特，在对每个512比特分别进行扩展和迭代压缩。
前一个分组的结果会参与下一个分组的迭代压缩计算。
经过一连串的迭代计算后，最终寄存器中的结果为SM3算法处理得到的杂凑值。
2. 相关符号和函数
2.1 一些符号定义
| mod | 模运算 |
|---|---|
| \(\land\) | 32比特与运算 |
| \(\vee\) | 32比特或运算 |
| \(\neg\) | 32比特非运算 |
| \(\oplus\) | 32比特异或运算 （由于输入法打不出这个符号，因此下面的配图里用\(xor\)代替了） |
| \(+\) | \(mod2^{23}\)算数加运算 |
| \(\lll k\) | 循环左移k比特运算 |
| \(\leftarrow\) | 左向赋值运算符 |
2.2 一些固定值和函数
初始值：
\(IV = 7380166f\ 4914b2b9\ 172442d7\ da8a0600\ a96f30bc\ 163138aa\ e38dee4d\ b0fb0e4e\)
常量：
\(T_j=\begin{cases} 79cc4519 & 0 \le j\le 15 \\ 7a879d8a & 16 \le j \le 63 \end{cases}\)
布尔函数：
\(FF_j(X,Y,Z)=\begin{cases}X\oplus Y\oplus Z & 0\le j\le 15 \\ (X\land Y)\vee (X\land Z)\vee (Y\land Z) & 16\le j \le 63\end{cases}\)
\(GG_j(X,Y,Z)=\begin{cases}X\oplus Y\oplus Z & 0\le j\le 15 \\ (X\land Y)\vee (\neg X\land Z) & 16\le j \le 63\end{cases}\)
式中\(X,Y,Z\)为字。
置换函数：
\(P_0(X) = X\oplus (X\lll 9)\oplus (X\lll 17)\)
\(P_1(X) = X\oplus (X\lll 15)\oplus (X\lll 23)\)
式中\(X\)为字。
3. 算法流程
3.1 填充
假设消息\(m\)的长度为l比特。
首先将比特“1”添加到消息的末尾，再添加k个"0",k是满足\(l+1+k\equiv 448 mod 512\)的最小非负整数。
然后再添加一个64位比特串，该比特串是长度\(l\)的二进制表示。
填充后的消息\(m^{'}\)的比特长度为512的倍数。
3.2 分组
将填充后的消息\(m^{'}\)按512比特进行分组：\(m'=B^{0}B^{1}\dots B^{n-1},n=(l+k+65)/512\)
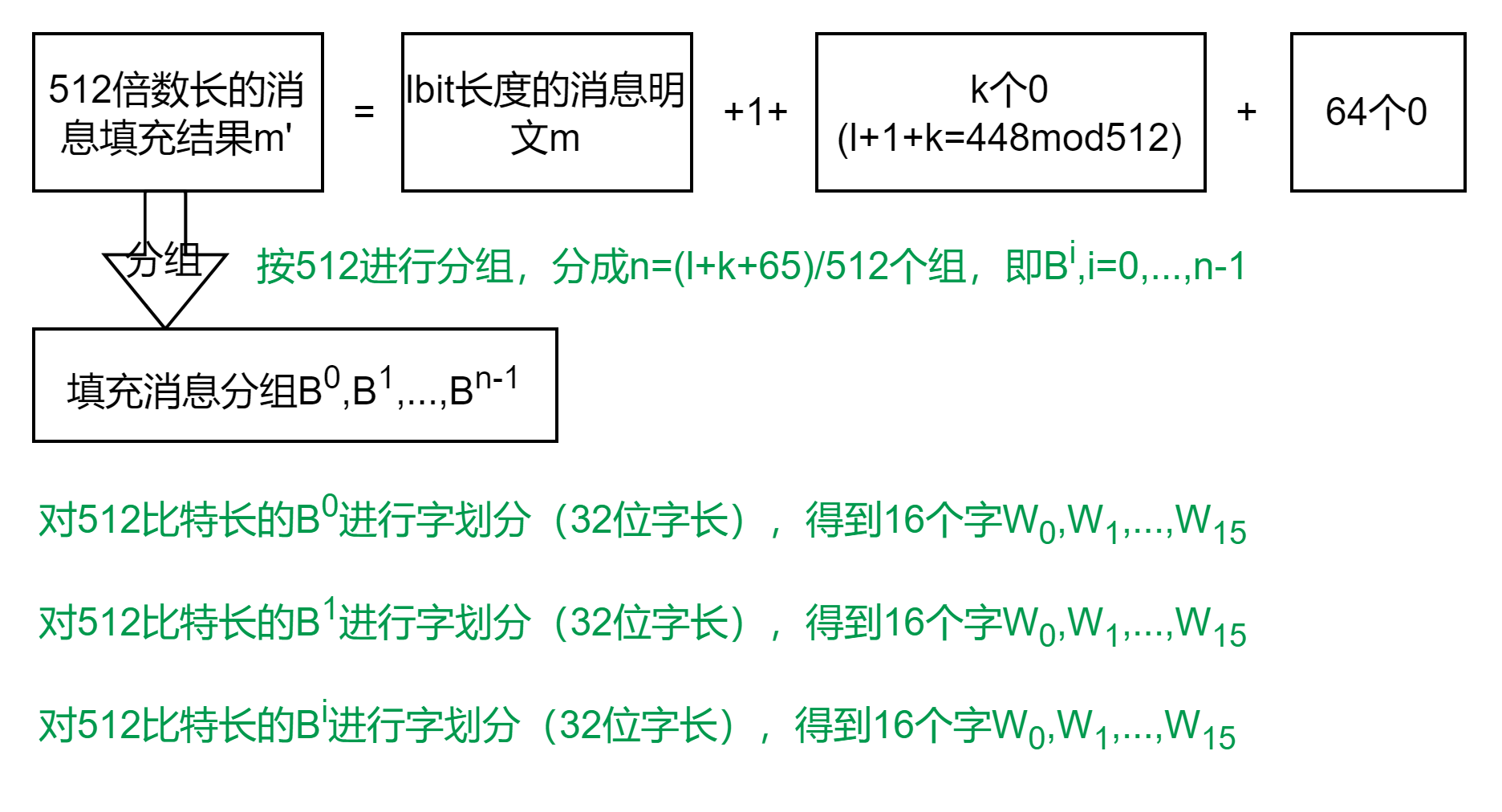
3.3 迭代压缩
3.3.1 消息扩展
将消息分组\(B^{i}\)按以下方法扩展生成132个字\(W_0,W_1,\dots,W_{67},W_0^{'},W_1^{'},\dots，W_{63}^{'}\)。
每一个分组\(B^i\)都需要扩展成这么多的字，每一个结果都会作为压缩函数的中间参数参与迭代计算。
a) 将消息分组\(B^i\)划分为16个字\(W_0,W_1,\dots,W_{15}\)；
b) FOR j=16 TO 67
\(W_j \leftarrow P_1 (W_{j-16}\oplus W_{j-9}\oplus (W_{j-3}\lll 15))\oplus(W_{j-13}\lll 7)\oplus W_{j-6}\)
ENDFOR
c) FOR j=0 TO 63
\(W_j^{'}=W_j \oplus W_{j+4}\)
ENDFOR
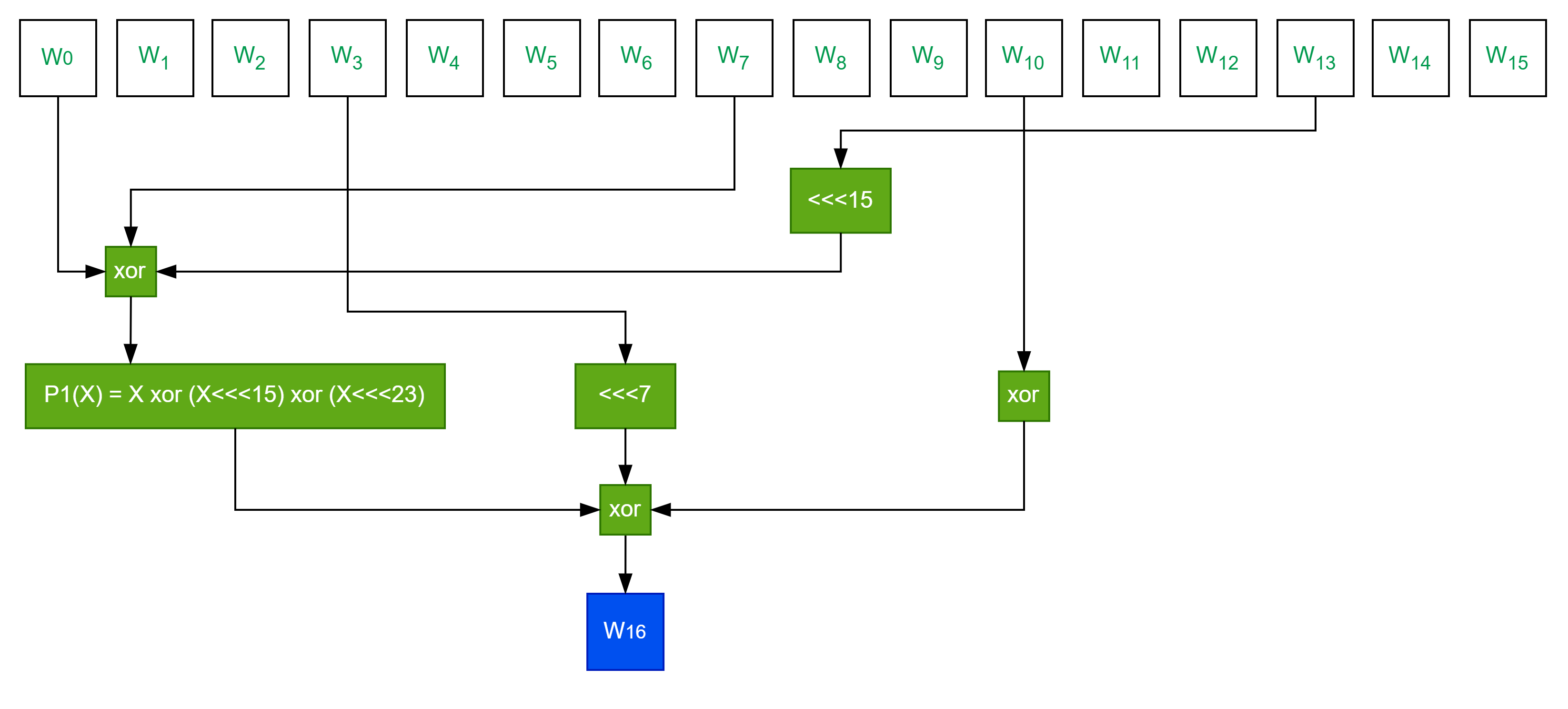
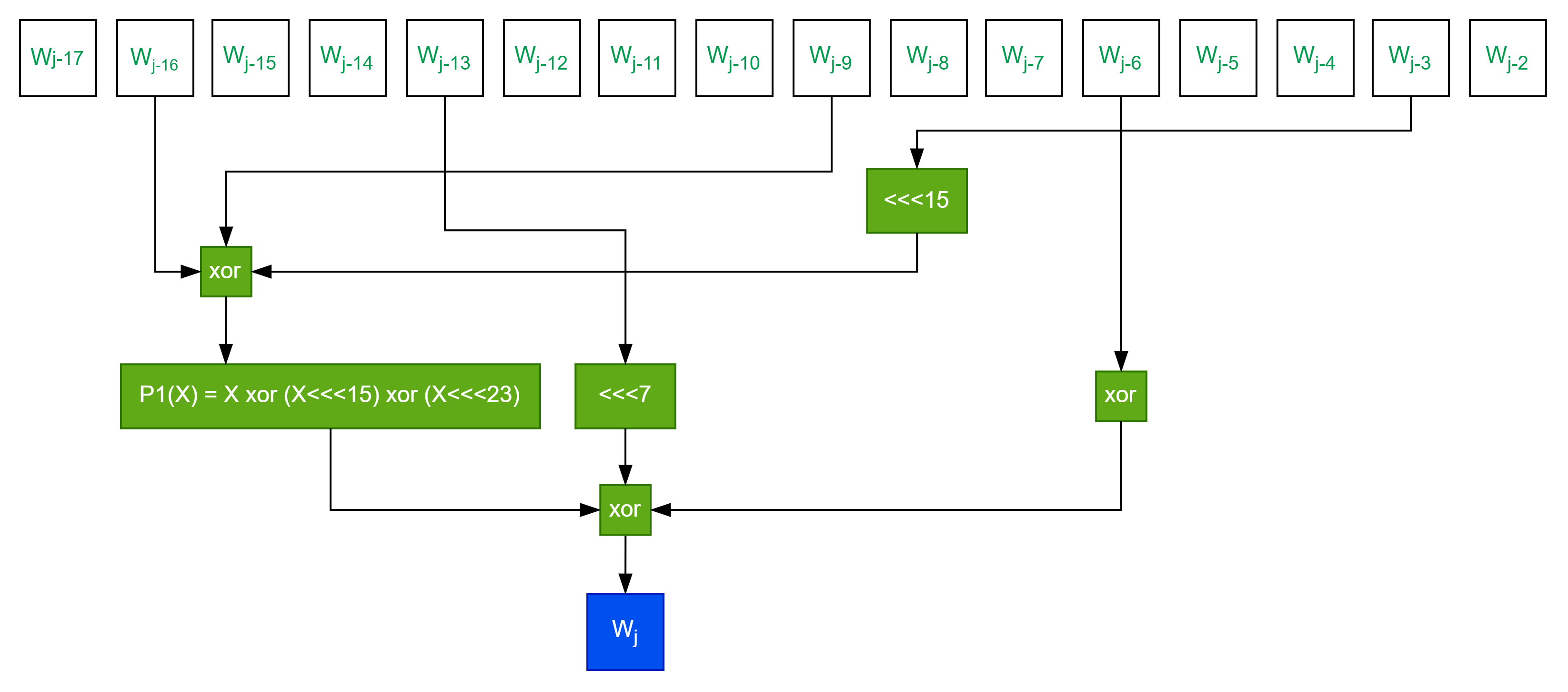
3.3.2 压缩函数
令A,B,C,D,E,F,G,H为字寄存器，SS1, SS2, TT1, TT2为中间变量，压缩函数\(V^{i+1}=CF(V^{(i)},B^{(i)}),0\le i\le n-1\)
计算过程如下：
\(ABCDEFGH \leftarrow V^{(i)}\)
FOR j=0 TO 63
$SS1 \leftarrow ((A\lll 12)+E+(T_j \lll j)) \lll 7 $
\(SS2 \leftarrow SS1 \oplus (A\lll 12)\)
\(TT1 \leftarrow FF_j (A,B,C)+D+SS2+W_j^{'}\)
\(TT2 \leftarrow (E,F,G)+H+SS1+W_j\)
\(D \leftarrow C\)
\(C \leftarrow B\lll 9\)
\(B \leftarrow A\)
\(A \leftarrow TT1\)
\(H \leftarrow G\)
\(G \leftarrow F \lll 19\)
\(F \leftarrow E\)
\(E \leftarrow P_0(TT2)\)
ENDFOR
\(V^{i+1} \leftarrow ABCDEFGH \oplus V^{(i)}\)
其中，字的存储为大端（big-endian）格式。
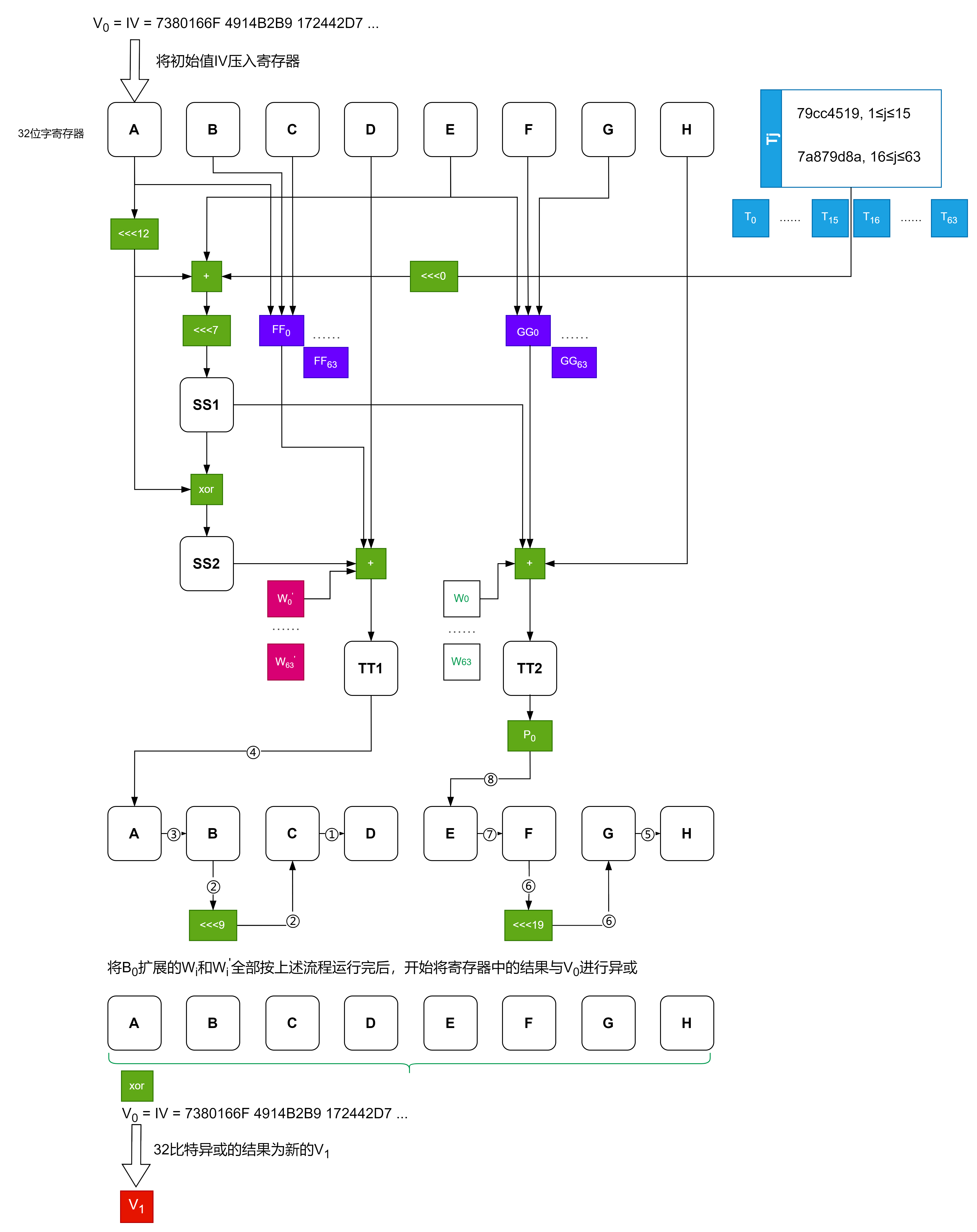
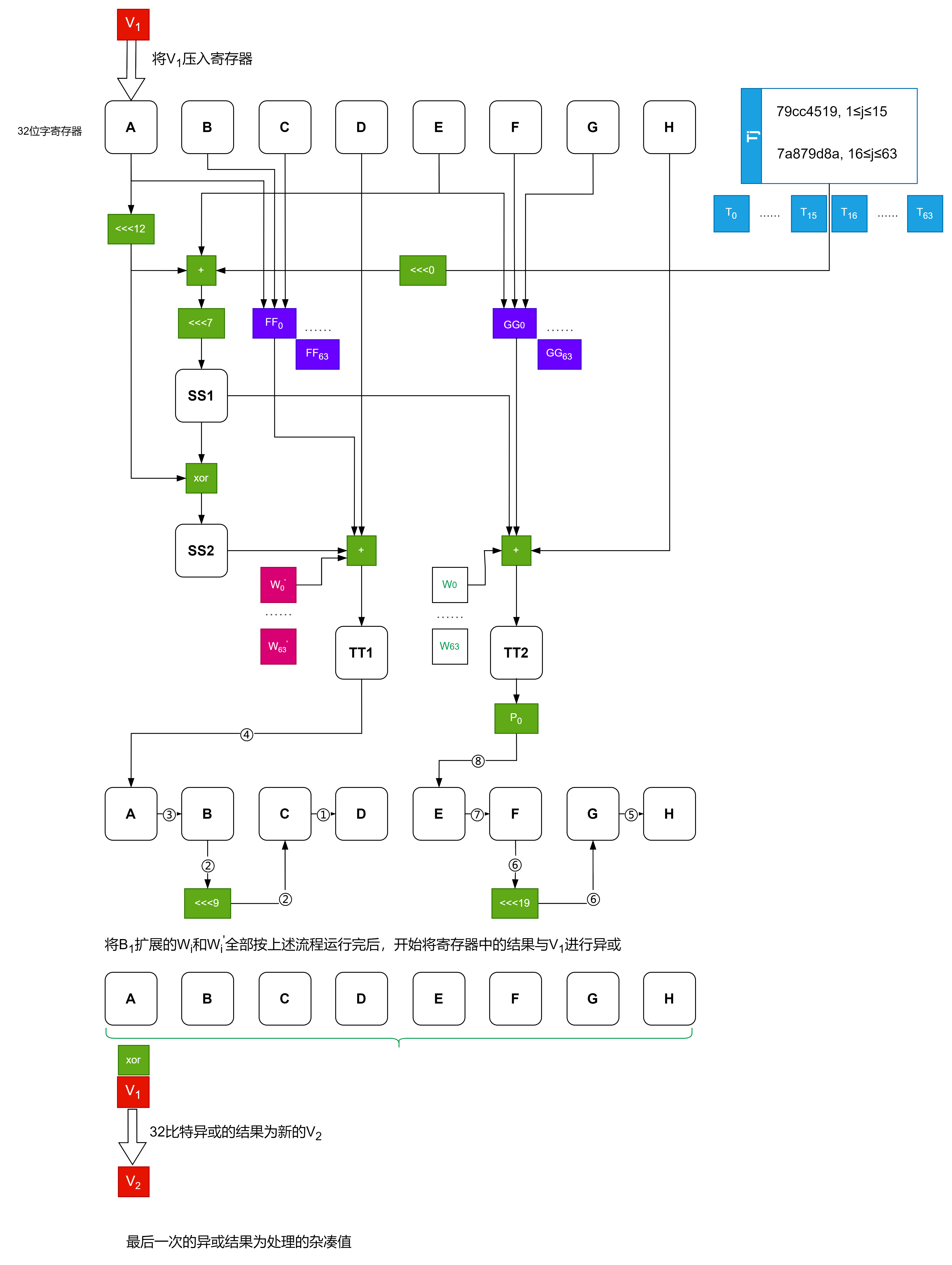
3.3.3 杂凑值结果
\(ABCDEFGH\leftarrow V^{(n)}\)
输出256比特的杂凑值\(y=ABCDEFGH\)。
