可能是多项式模板全家桶/(不到)万字长文/或许是较好理解的板子讲解/阅读本文约需9分钟

可能是多项式模板全家桶

(不到)万字长文

或许是较好理解的板子讲解

本文无代码 否则您将学习每天一个常数爆炸小技巧

qwq

阅读本文约需9分钟:

前置知识:

复数

虚数单位

虚数单位\(i=\sqrt{(-1)}\)

定义

复数是形如\(a+bi\)的数

运算

加法

复数 \(x=(a+bi),y=(c+di)\)的和定义为 \(x+y=(a+bi)+(c+di)=a+c+(d+b)i\)

乘法

复数 \(x=(a+bi),y=(c+di)\)的积定义为\(xy=(a+bi)(c+di)=ac-bd+(ad+cb)i\)

发现复数可以用座标表示 如\(x=(a+bi)\)可表示为\((a,b)\) 这样也可以表示为向量 我们记模长为\(r=\sqrt{a^2+b^2}\) 俯角为\(\alpha\) 于是向量表示为\((rcos\alpha,rsin\alpha)\) 发现一个性质 两向量的积\((rcos\alpha,rsin\alpha)(Rcos\beta,Rsin\beta)\)等于\((rRcos(\alpha+\beta),rRsin(\alpha+\beta))\) 模长相乘俯角相加

单位根

单位根是形如这样的方程的所有的根:

\[x^n=1 \]

根据算数基本定理 这样的根在复数域上有n个

我们记第一个为\(w_n\) 它应当是某个复数 我们知道 复数乘法满足模长相差俯角相加 那么它在复数域上的几何表示就是单位圆\(n\)等分后从(0,1)开始转的第一份

我么发现 第一个单位根的k次方\((0<=k<=n-1)\)也是一个单位根

单位根具有以下性质 希望读者自行验证:

1 \(w_n^k=w_{n/2}^{k/2}\)

2 \(w_n^{k+n}=w_n^k\)

3 \(w_n^{k+n/2}=-w_n^k\)

4 \(w_n^0=w_n^n=1\)

原根

阶

对于一个数 a 一个模数 p 存在最小的 y使得

\[a^y\equiv1\pmod p \]

定义

若对于一个模数p 存在一个a使得a对p的阶等于phi(p) 那么a就叫做p的原根

性质

\(a^0,a^1,a^2,⋯,a^{\varphi(p)}\) 模 p 两两不同余，且 \(a^k\equiv a^{k+\varphi(p)}\pmod p\)

泰勒展开

回忆微分法

熟知对于一点\(x_0\) 我们试图寻找其邻域的某点\(x\)及其函数值\(f(x)\) 我们应该构造关于\((x-x_0)\)的一次多项式 \(p(x)=f(x_0)+f'(x_0)(x-x_0)\) 使得\(p'(x-x_0)=f'(x_0)\)

发现该微分法存在以下突出问题:

• 精度损失不确定
• 精度损失较大

于是我们期望能够得到一个多项式\(p(x)\) 使得

\[p(x)=\sum_{i=0}^{n}a_i(x-x_0)^i \]

并且\(p^{(i)}(x-x_0)=f^{(n)}(x_0)\)

于是设x=0连续求导后 \(a_i=\frac{f^{(i)}(x)}{i!}\)

牛顿迭代

发现我们在对精度要求不高时可以使用导数(直线)近似代替原函数来近似求解函数根

若对精度要求更高重复使用即可

这样我们引出迭代公式

\[在(x_0,f(x_0))处的切线方程为y-f(x_0)=f'(x_0)(x-x_0) \\ 于是x=x_0-\frac{f(x_0)}{f'(x_0)} \]

FFT

fft是解决多项式乘法(加法卷积)的一种方法

我们发现加法卷积复杂度极高 这是不能被我们承受的

考虑讲要卷的两个多项式求出点值表示 然后把点值相乘 然后插值回答案多项式

DFT

dft是进行多项式多点求值的算法 我们发现多项式

\[f(x)=a_0+a_1x^1+a_2x^2+a_3x^3+a_4x^4+a_5x^5... \\ 可以拆分为 \\ fl(x)=a_0+a_2x^1+a_4x^2+a_6x^3... \\和\\ fr(x)=a_1+a_3x^1+a_5x^2+a7x^3... \\于是\\ f(x)=fl(x^2)+xfr(x^2) \\我们试着将单位根带入\\ f(w_n^k)=fl(w_n^{2k})+w_n^kfr(w_n^{2k})=fl(w_{n/2}^{k})+w_n^kfr(w_{n/2}^{k}) \\并且有\\ f(w_n^{k+n/2})=fl(w_n^{2k+n})+w_n^{k+n/2}fr(w_n^{2k+n})=fl(w_{n/2}^{k})-w_n^kfr(w_{n/2}^{k}) \]

我们可以分治求解 复杂度\(O(nlogn)\)

IDFT

idft是进行多项式多点插值的算法

\((y_0,y_1,y_2...y_{n-1})\)为\((a_0,a_1,a_2,...a_{n-1})\)的点值表示

那么设另一组数列\(\{c_k\}\)满足\(c_k=\sum_{i=0}^{n-1}y_i(w_n^{-k})^i\)

那么

\[c_k=\sum_{i=0}^{n-1}y_i(w_n^{-k})^i \\ =\sum^{n-1}_{i=0}(\sum^{n-1}_{j=0}a_j(w^i_n)^j)(w_n^{-k})^i \\ =\sum^{n-1}_{i=0}(\sum^{n-1}_{j=0}a_j(w^j_n)^i)(w_n^{-k})^i \\ =\sum^{n-1}_{i=0}\sum^{n-1}_{j=0}a_j(w^{j-k}_n)^i \\ =\sum^{n-1}_{j=0}a_j(\sum^{n-1}_{i=0}(w^{j-k}_n)^i) \]

那么 我们发现 对于后半个合式 若\(j=k\) 取值为\(n\)

若不等呢:

设\(j-k=s\)

利用等比数列求和公式

后半个合式等于\(\frac{(w_n^s)^n-1}{w_n^s}\)

上半部等于0

于是\(c_k=na_k\)

把n除过去即可

NTT

发现整个fft的过程中都是在做实数运算 精度误差存在且不小 并且复数运算很慢 甚至某些时候需要蝴蝶优化减少递归带来的巨大常数 我们的推导用到了单位根的如下性质:

1 \(w_n^k=w_{n/2}^{k/2}\)

2 \(w_n^{k+n}=w_n^k\)

3 \(w_n^{k+n/2}=-w_n^k\)

4 \(w_n^0=w_n^n=1\)

5 n次方内互不相等

惊喜的发现这些性质在模意义下的时原根也具有

于是在代码中将复数全部换为原根即可

FWT

fwt是用于解决一类位运算卷积的算法

基本思想与概览

熟知fft是线性的 我们期望fwt也可以得到一个线性函数

我们首先写出位运算卷积的一般形式:

\[S[k]=\sum_{i\oplus j=k}A[i]B[j] \]

记作

\[S=A*B \]

其中\(\oplus\)是某种位运算

设FWT变换系数为\(c(i,j)\) 我们设FWT(A)是A经过FWT变换后的数列

需满足:

\[A*B=C \iff FWT(A)\cdot FWT(B)=FWT(B) \]

于是

\[FWT(A)[i]=\sum^{n-1}_{j=0}c(i,j)A_j \]

依

\[FWT(A)\cdot FWT(B)=FWT(B) \]

得

\[FWT(A)[i]FWT(B)[i]=FWT(c)[I] \\ \sum^{n-1}_{j=0}c(i,j)A[j]\sum^{n-1}_{k=0}c(i,k)B[k]=\sum^{n-1}_{p=0}c(i,p)C[p] \\ \sum^{n-1}_{j=0}\sum^{n-1}_{k=0}c(i,j)c(i,k)A[j]B[k]=\sum^{n-1}_{p=0}c(i,p)C[p] \]

依

\[C[p]=\sum_{t_1\oplus t_2=p}A[t_1]B[t_2] \]

又得

\[\sum^{n-1}_{p=0}c(i,p)C[p]=\sum^{n-1}_{p=0}c(i,p)\sum_{t_1\oplus t_2=p}A[t_1]B[t_2] \\ \sum^{n-1}_{j=0}\sum^{n-1}_{k=0}c(i,j)c(i,k)A[j]B[k]=\sum^{n-1}_{p=0}c(i,p)\sum_{t_1\oplus t_2=p}A[t_1]B[t_2] \\ \sum^{n-1}_{j=0}\sum^{n-1}_{k=0}c(i,j)c(i,k)A[j]B[k]=\sum^{n-1}_{t_1=0}\sum_{t_2=0}^{n-1}A[t_1]B[t_2]c(i,t_1\oplus t_2) \]

对比发现只需使\(c(i,j)c(i,k)=c(i,j\oplus k)\)

另外 由位运算只考虑独立位的特殊性 我们有:

对于一个二进制数a 它的每一位表示为\(a_0,a_1,a_2,a_3,a_4,....\)

设我们已经知道所有满足要求的c([0,1],[0,1])

那么

\[c(i,j)=c(i_0,j_0)c(i_1,j_1)c(i_2,j_2),... \]

于是

\[\prod_p c(i_p,j_p)c(i_p,k_p)=\prod_p c(i_p,j_p\oplus k_p) \\ c(i,j)c(i,k)=c(i,j\oplus k) \]

由此 只要我们构造出单位的c函数 我们就可以构造出所有数的c函数

我们如何快速求位运算卷积呢

依然考虑分治

首先折半

\[FWT(A)[i]=\sum_{j=0}^{(n/2)-1}c(i,j)A[j]+\sum_{j=(n/2)}^{n-1}c(i,j)A[j] \]

对于i,j的首位 我们分开考虑 设i'为i去掉二进制首位的数

于是

\[=\sum_{j=0}^{(n/2)-1}c(i_0,j_0)c(i',j')A[j]+\sum_{j=(n/2)}^{n-1}c(i_0,j_0)c(i',j')A[j] \\ =c(i_0,0)\sum_{j=0}^{(n/2)-1}c(i',j')A[j]+c(i_0,1)\sum_{j=(n/2)}^{n-1}c(i_0,j_0)c(i',j')A[j] \]

加号两边柿子分别递归处理 我们成功缩小了问题的规模

一些例子

针对不同位运算 我们需要构造出不同的c([0,1],[0,1]) 再结合上面的推导 问题就得到了解决

Or卷积

c([0/1],[0/1])的矩阵

\[\begin{bmatrix} c(0,0)&c(0,1)\\ c(1,0)&c(1,1) \end{bmatrix} \]

应满足条件 \(c(i,j)c(i,k)=c(i,j|k)\)

• \(c(0,0)=c(0,0|0)\Rightarrow c(0,0)=1或0\)
• \(c(0,1)c(0,0)= c(0,1|0)\Rightarrow c(0,1)=0或c(0,0)=c(0,1)=1\)
• \(c(1,1)c(1,0)=c(1,1|0)\Rightarrow c(1,1)=0或c(1,0)=c(1,1)=1\)

并且这个矩阵应当是有逆的 否则就无法回去 我们最终选取

\(c(0,0)=1,c(0,1)=0,c(1,0)=1,c(1,1)=1\)

逆变换其实只需矩阵求逆即可

或者考虑算式的反算式即可

那么同理对于

And卷积

有矩阵

\[\begin{bmatrix} 1&1\\ 0&1 \end{bmatrix} \]

和

Xor卷积

有矩阵

\[\begin{bmatrix} 1&1\\ 1&-1 \end{bmatrix} \]

既得易见平凡 仿照上例显然 留作习题答案略 读者自证不难

反之亦然同理 推论自然成立 略去过程Q E D 由上可知证毕

​ 西江月/证明

多项式乘法逆

多项式求逆即对于多项式\(f(x)\)

我们求一个\(g(x)\)

使得

\[g(x)*f(x)\equiv1 \pmod {x^n} \]

倍增法

边界

当界为\(\pmod{x^1}\) 即多项式只有常数项时 直接数字逆元即可

转移

假设我们得到了\(T(x)\equiv F(x)^{-1} \pmod {x^{n/2}}\)

显然有\(G(x)\equiv T(x)\pmod{x^{n/2}}\)

那么 \((G(x)-T(x))^2\equiv0\pmod{x^n}\)

\(G(x)^2-2G(x)T(x)+T(x)^2\equiv0\pmod{x^n}\)

同乘\(F(x)\)

\(R(x)-2G(x)-G(x)^2F(x)\equiv0\pmod{x^n}\)

运用多项式乘法倍增即可

多项式开根

给定\(g(x)\) 求\(f(x)\)满足

\[f^2(x)\equiv g(x)\pmod{x^n} \]

倍增法

假设已求出\(g(x)\)在模\(x^{[n/2]}\)意义下的平方根\(f_0(x)\) 则有

\[f_0^2(x)\equiv g(x) \pmod{x^{[n/2]}} \\ f_0^2(x)-g(x)\equiv 0\pmod{x^{[n/2]}} \\ (f_0^2(x)-g(x))^2\equiv 0\pmod{x^{n}} \\ (f_0^2(x)+g(x))^2\equiv 4f_0^2(x)g(x)\pmod{x^{n}} \\ (\frac{f_0^2(x)+g(x)}{2f_0(x)})\equiv g(x)\pmod{x^{n}} \\ \frac{f_0^2(x)+g(x)}{2f_0(x)}\equiv f(x) \pmod{x^n} \\ \frac 1 2f_0(x)+2^{-1}f_0^{-1}(x)g(x)\equiv f(x) \pmod{x^n} \]

多项式除法

给定多项式\(f(x),g(x)\) 求\(g(x)\)除\(f(x)\)的商\(q(x)\)和余数\(r(x)\)

若能消去\(r(x)\)的影响则可直接多项式乘法逆

考虑构造

\[f_r(x)=x^nf(\frac 1 x) \]

容易发现其为反转\(f(x)\)系数

设\(n=\deg f,m=\deg g\)

则

\[f(x)=q(x)g(x)+r(x)\Rightarrow \\ x^nf(\frac 1 x)=x^{n-m}q(\frac 1 x)x^mg(\frac 1 x)+x^{n-m+1}x^{m-1}r(\frac 1 x) \\ f_r(x)=q_r(x)g_r(x)+x^{n-m+1}r_r(x) \\ 于是 \\ f_r(x)\equiv q_r(x)g_r(x)\pmod{x^{n-m+1}} \]

多项式求逆\(g_r(x)\)即可 然后求出\(q_r(x)\)和\(r_r(x)\)

多项式ln

给定多项式\(f(x)\) 求模\(x^n\)意义下\(lnf(x)\)

解法本质就是暴力

对多项式先求导再积分即可

\[\frac {\text{d}\ln f(x)}{dx}\equiv \frac {1}{f(x)} f'(x)\pmod{x^n} \]

多项式牛顿迭代

对于给定\(g(x)\) 求\(f(x)\) 使得其满足\(g(f(x))\equiv 0 \pmod{ x^n}\)

假设已经得到了模\(x^{[n/2]}\)次方的解\(f_0(x)\) 要求模\(x^n\)的解\(f(x)\)

跟据定义我们知道 \(f(x)\)与\(f_0(x)\)在前\([n/2]-1\)位上相等

那么我们写出\(g(f(x))\)在\(f_0(x)\)处的泰勒展开

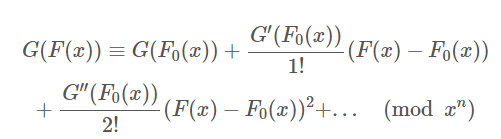
发现从第三项往后全部被模掉了 没有意义 我们即可直接用牛顿迭代式计算

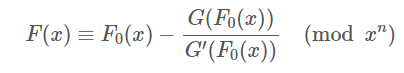
应用

多项式求逆

给定多项式\(h(x)\) 有方程

\[g(f(x))=\frac1 {f(x)}-h(x)\equiv0\pmod0 \]

应用牛顿迭代有

\[\begin{aligned} f\left(x\right)&\equiv f_{0}\left(x\right)-\frac{\frac{1}{f_{0}\left(x\right)}-h\left(x\right)}{-\frac{1}{f_{0}^{2}\left(x\right)}}&\pmod{x^{n}}\\ &\equiv 2f_{0}\left(x\right)-f_{0}^{2}\left(x\right)h\left(x\right)&\pmod{x^{n}} \end{aligned} \]

多项式开方

给定多项式\(h(x)\) 有方程

\[g(f(x))=f^2(x)-h(x)\equiv0\pmod{x^n} \]

应用牛顿迭代有

\[f(x)\equiv f_0(x)-\frac{f_0^2(x)-h(x)}{2f_0(x)}\pmod{x^n} \\ \equiv\frac{f_0^2(x)+h(x)}{2f_0(x)}\pmod{x^n} \]

多项式exp

给定多项式\(h(x)\) 有方程

\[g(f(x))=\ln f(x)-h(x)\pmod {x^n} \]

应用牛顿迭代有

\[f(x)\equiv f_0(x)-\frac{\ln f_0(x)-h(x)}{\frac1{f_0(x)}} \\ f_0(x)(1-ln f_0(x)+h(x))\pmod{x^n} \]