澡堂游记DAY2

5月2日主要内容为树形dp与状压dp

感觉今天讲的也没什么可写的qwq

但是插头dp我是真没听懂 在此做一些整理

本篇依例题https://www.luogu.com.cn/problem/P5056【模板】插头dp讲解

插头dp是为了解决网格链接性问题的一种算法 由某thu爷发明

要素

轮廓线

插头dp的dp顺序时从上到下 从左向右进行的
我们需要一条称之为轮廓线的分界线区分已进行完dp的区域与未进行完dp的区域
如图所示：

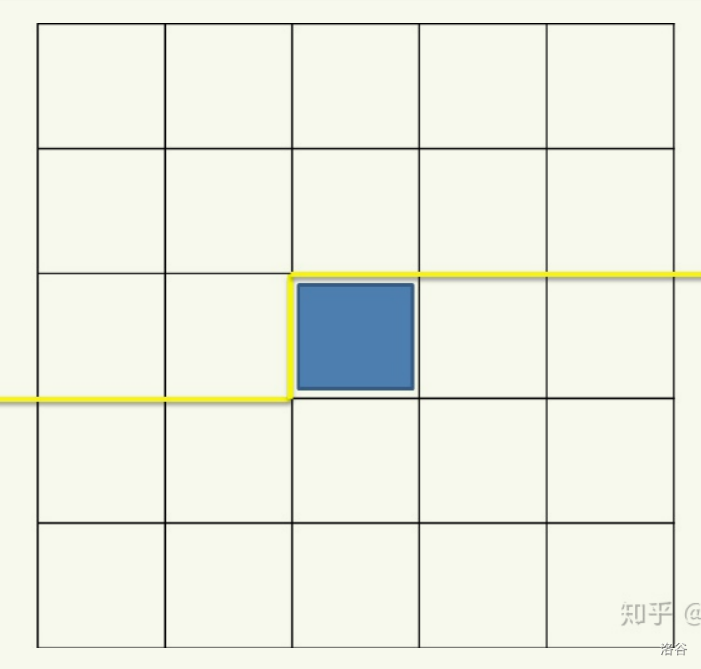
黄线即为轮廓线
可以发现 轮廓线长度即m+1
我们的大多数dp操作都是以轮廓线为准进行的

插头

插头表示不同方块的见的链接状态
比如格子[i][j]与格子[i][j+1]连通，那么[i][j]就有一个右插头[i][j+1]就有一个左插头

注意插头一定是成对存在的，它是一种实际状态，即两个格子之间确实连通了，并不是一种“将要连通过去”的虚拟状态。简单的说，产生一对插头，必须要有两个格子“两情相悦”

轮廓线的状态

容易看出，例题轮廓线上的插头一定是偶数个，我们可以让插头两两配对（因为只有当插头上的点时偶数个时 下面的格子才会有可能链接

于是我们将轮廓线上的插头分为两类：左括号插头和右括号插头

一个左括号插头和一个右括号插头配对，当且仅当：当前状态下，在已考虑部分中，这两个插头所在格子已经连通

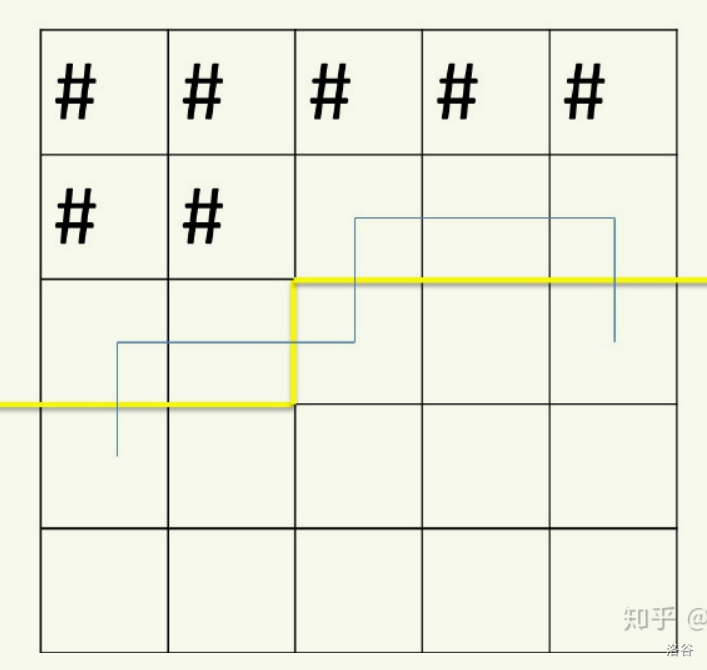
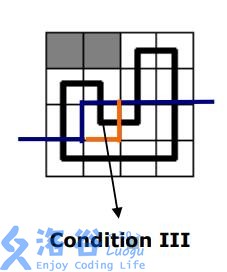
图中蓝线就是已考虑部分的一种可能的连通情况（也包括了轮廓线的插头情况），那么此时轮廓线的状态就是：(0)(0)

我们可以用三进制来表示轮廓线状态，0表示没有插头，1表示左插头，2表示右插头

三进制的运算非常慢，我们把它变成四进制，然后就可以进行位运算了

那么轮廓线的连通情况，状态最大值会高达\(4^{m+1}\) ，把\(m=12\)代入计算就是67108864，如果要开那么大的数组，显然空间爆炸。幸运的是，在所有情况中，有效情况的数量其实只有20万左右，因此我们可以开一个20万的数组，然后搞一个哈希表来对有效状态编号

当然，有一些题目不一定要求插头两两配对，比如Park II那道题，具体情况具体分析吧

转移

分情况讨论 以本例为例

合并两联通分量

如果当前轮廓线上既有右插又有下插，那你只能当前格做左插和上插，要不然就不是回路了。

然后如果右插和下插联通，那这种情况只能是在最后一个非障碍格是合法的。

不连通的话，当然这样做会把他们变联通，看图：

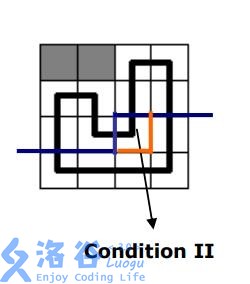
新建一个连通分量

这个情况只出现在转移位置的轮廓线上没有下插头和右插头。

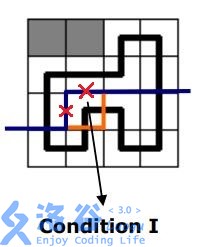
如图。然后我们只有一种转移方式就是当前格做右插头和下插头。

括号表示法就是新建一对紧挨着的左右括号。最小表示法就直接解码重编一下。

保持原来的连通分量

当轮廓线上只有下插或者右插，就只能当前格做一个左插/上插来满足回路性质，剩下一个插头是随便安排的。

图：

括号表示法的话就把下插/右插对应的括号移到你加的插头上就行了。

最小表示法也类似，把下插/右插位置的记号移到你加的插头对应位置就行（因为是延续了一个连通分量）。

注意当从一行的最后一个格子转移到下一行的第一个格子的时候，轮廓线需要特殊处理。这个看代码最好解释了。

（还要多啰嗦一句，一般状态编码的左右和轮廓线的左右是反着对应的……也就是编码最右面一位是对应轮廓线最左面格子）

( 这样大概比较好写? )

代码实现略