题解 小p的新牧场 详解斜率优化

题面

背景

小 P 是个特么喜欢玩 MC 的孩纸。。。

描述

小 P 在 MC 里有 n 个牧场，自西向东呈一字形排列（自西向东用 1…n 编号），于是 他就烦恼了：为了控制这 n 个牧场，他需要在某些牧场上面建立控制站，每个牧场 上只 能建立一个控制站，每个控制站控制的牧场是它所在的牧场一直到它西边第一个控 制站 的所有牧场（它西边第一个控制站所在的牧场不被控制）（如果它西边不存在控制站， 那么它控制西边所有的牧场），每个牧场被控制都需要一定的花费（毕竟在控制站到 牧 场间修建道路是需要资源的嘛~），而且该花费等于它到控制它的控制站之间的牧场 数目 （不包括自身，但包括控制站所在牧场）乘上该牧场的放养量，在第 i 个牧场建立 控制 站的花费是 ai，每个牧场 i 的放养量是 bi，理所当然，小 P 需要总花费最小，但 是小 P 的智商有点不够用了，所以这个最小总花费就由你来算出啦。

输入格式

第一行一个整数 n 表示牧场数目 第二行包括 n 个整数，第 i 个整数表示 ai 第三行包括 n 个整数，第 i 个整数表示 bi 输出格式 只有一行，包括一个整数，表示最小花费

样例输入

4

2 4 2 4

3 1 4 2

样例输出

9

样例解释

选取牧场 1，3，4 建立控制站，最小费用为 2+( 2 + 1 * 1 ) + 4 = 9。

数据范围与约定

对于 10%的数据，1 <= n <= 10 对于 30%的数据，1 <= n <= 1000 对于 100%的数据，1 <= n <= 1000000 , 0 < ai,bi <= 10000

O(n³)做法

显而易见 设 dp[ i ] 表示到 i 为止的最小费用 转移时只需枚举上一个控制站 j 即可

方程

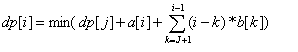
O(n²)做法

化简原方程发现：

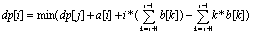
设su[ i ]为b[ i ]的前缀和 ts[ i ]为b[ i ] * i 的前缀和

则方程可表示为

dp[ i ] = min( dp[ j ] + i *（su[ i - 1 ] - su[ j ]）- ( ts[ i - 1 ] - ts[ j ] ) + a[ i ] )

因i在枚举j时相当于定值 进一步有

dp[ i ] = min( dp[ j ] - i * su[ j ] + ts[ j ] ) + i * su[ i - 1 ] - ts[ i - 1 ] + a[ i ] 

枚举j即可

O(n) （斜率优化）

将min函数忽略 j的相关项移至等号左边  i与j的乘积项仍保留在右边

ts[ j ] + dp[ j ] = i * su[ j ]- i * su[ i - 1 ] + ts[ i - 1 ] - a[ i ] + dp[ i ]

可以发现 这是一个以i为斜率的一次函数 左边视为纵坐标 su[ j ]为横坐标 i即为斜率  - i * su[ i - 1 ] + ts[ i - 1 ] - a[ i ] + dp[ i ]则为截距

使dp[i]最小 即使截距最小

我们要做的 就是找到哪个j使得截距最小

因为纵坐标单调上升 横坐标也单调上升 斜率为定值

显而易见 用单调队列维护一个关于横坐标与纵坐标的下凸包 

并使下凸包两点间的斜率大于i 最左边的点即为所要找的j

再将i插入单调队列 将队尾与i不符合下凸包性质的点弹出使i插入后队列仍满足下凸包性质即可 

代码

#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
using namespace std;
long long a[1000001],T[1000001],n,dp[1000001],su[1000001],ts[1000001];
long long dl[1000001];
double count(long long a,long long b)
{
    return 1.0*(ts[a]+dp[a]-(ts[b]+dp[b]))/(double)(su[a]-su[b]);
}
int  main()
{
    //freopen("pasture.in","r",stdin);
    //freopen("pasture.out","w",stdout);
    cin>>n;
    memset(dp,0x3f,sizeof(dp));
    for(long long i=1;i<=n;i++)
        scanf("%lld",&a[i]);
    for(long long i=1;i<=n;i++)
        scanf("%lld",&T[i]);
    for(long long i=1;i<=n;i++)
    su[i]=su[i-1]+T[i];
  for(long long i=1;i<=n;i++)
    ts[i]=ts[i-1]+1ll*i*T[i];
    long long rt=1,lf=1;
    dp[0]=0;
  for (long long i=1;i<=n;i++)
    { 
        while(i>=count(dl[lf],dl[lf+1])&&rt>lf)    lf++;
        dp[i]=dp[dl[lf]]+i*(su[i-1]-su[dl[lf]])-ts[i-1]+ts[dl[lf]]+a[i];
        while(lf<rt&&count(i,dl[rt])<=count(dl[rt],dl[rt-1])) rt--;;
        dl[++rt]=i;
  }
    cout<<dp[n];
    return 0;
}