R_Studio(教师经济信息)逻辑回归分析的方法和技巧

 

　　

使用R语言对"教师经济信息"进行逻辑回归分析

 

　　（1）按3:1的比例采用简单随机抽样方法，创建训练集和测试集

　　（2）用训练集创建逻辑回归模型

　　（3）用测试集预测贷款结果，并用table统计分类的最终结果

　　（4）计算 评价指标：总体准确率、准确（分类）率、误分类率、正例的覆盖率、正例的命中率、负例的命中率

　　（5）采用逐步寻优法后，重新用测试集预测贷款结果，并评估模型

 

 

setwd('D:\\data')

list.files()

dat=read.csv(file="bankloan.csv",header=TRUE)[2:701,]

#数据命名
colnames(dat)<-c("x1","x2","x3","x4","x5","x6","x7","x8","y")
#logistic回归模型

n=nrow(dat)

#按3:1的比例采用简单随机抽样方法，创建训练集和测试集
split<-sample(n,n*(3/4))
traindata=dat[split,]
testdata=dat[-split,]

#用训练集创建逻辑回归模型
glm=glm(y~x1+x2+x3+x4+x5+x6+x7+x8,family=binomial(link=logit),traindata)
summary(glm)

#用测试集预测贷款结果
predict=predict(glm,type="response",newdata=testdata)
res1<-data.frame(testdata$y,predict=ifelse(predict>0.5,1,0))

#用table统计分类的最终结果
table(res1)
test<-table(res1)  
a<-test[1,1]
b<-test[1,2]
c<-test[2,1]
d<-test[2,2]

#准确（分类）率=正确预测的正反例数/总数：
Accuracy<-(a+d)/(a+b+c+d)
#误分类率=错误预测的正反例数/总数：
Errorrate<-(b+c)/(a+b+c+d)

#正例的覆盖率=正确预测到的正例数/实际正例总数：
Recall<-d/(c+d)

#正例的命中率=正确预测到的正例数/预测正例总数：
Precision<-d/(b+d)
# 负例的命中率=正确预测到的负例个数/预测负例总数：
Negative<-a/(a+c)
print(data.frame(指标=c("准确率","误分类率","正例的覆盖率","正例的命中率","负例的命中率"),值=c(Accuracy,Errorrate,Recall,Precision,Negative)))



#####逐步寻优法
logit.step<-step(glm,direction="both")
summary(logit.step)
#####前向选择法
logit.step<-step(glm,direction="forward")
summary(logit.step)
#####后向选择法
logit.step<-step(glm,direction="backward")
summary(logit.step)

 

 

实现过程

 

（1）按3:1的比例采用简单随机抽样方法，创建训练集和测试集。

    split<-sample(n,n*(3/4))
    traindata=dat[split,]
    testdata=dat[-split,]

 

　　sample(x,size,replace=F)

　　x：数据集

　　size：从对象中抽出多少个数，size应该小于x的规模，否则会报错

　　replace：默认是F，表示每次​抽取后的数就不能在下一次被抽取；T表示抽取过的数可以继续拿来被抽取

 

（2）用训练集创建逻辑回归模型

    glm=glm(y~x1+x2+x3+x4+x5+x6+x7+x8,family=binomial(link=logit),traindata)
    summary(glm)

　　

　　glm(formula, family = gaussian, data, weights, subset,

    　　　　na.action, start = NULL, etastart, mustart, offset,

  　　 　　 control = list(...), model = TRUE, method = "glm.fit",

  　　 　　 x = FALSE, y = TRUE, contrasts = NULL, ...)

 

　　formula为拟合公式，与函数lm()中的参数formula用法相同;
　　family用于指定分布族，包括正态分布(gaussian)、二项分布(binomial)、泊松分布(poisson)和伪伽马分布(Gamma)；
　　分布族还可以通过选项link来指定连接函数，默认值为family=gaussian (link=identity),二项分布默认值为family=binomial(link=logit);
　　data指定数据集
　　offset指定线性函数的常数部分，通常反映已知信息
　　control用于对待估参数的范围进行设置 

 

（3）用测试集预测贷款结果，并用table统计分类的最终结果

    #用测试集预测贷款结果
    predict=predict(glm,type="response",newdata=testdata)
    res1<-data.frame(testdata$y,predict=ifelse(predict>0.5,1,0))

    #用table统计分类的最终结果
    table(res1)
    test<-table(res1)  

　　predict(model,newdata)

　　model：模型，把新的自变量按照变量名放在一个data frame里（newdata）

 

　　

 

 

（4）计算 评价指标：总体准确率、准确（分类）率、误分类率、正例的覆盖率、正例的命中率、负例的命中率

    a<-test[1,1]
    b<-test[1,2]
    c<-test[2,1]
    d<-test[2,2]

    #准确（分类）率=正确预测的正反例数/总数：
    Accuracy<-(a+d)/(a+b+c+d)
    #误分类率=错误预测的正反例数/总数：
    Errorrate<-(b+c)/(a+b+c+d)

    #正例的覆盖率=正确预测到的正例数/实际正例总数：
    Recall<-d/(c+d)

    #正例的命中率=正确预测到的正例数/预测正例总数：
    Precision<-d/(b+d)
    # 负例的命中率=正确预测到的负例个数/预测负例总数：
    Negative<-a/(a+c)
    print(data.frame(指标=c("准确率","误分类率","正例的覆盖率","正例的命中率","负例的命中率"),值=c(Accuracy,Errorrate,Recall,Precision,Negative)))

 

 

（5）采用逐步寻优法后，重新用测试集预测贷款结果，并评估模型

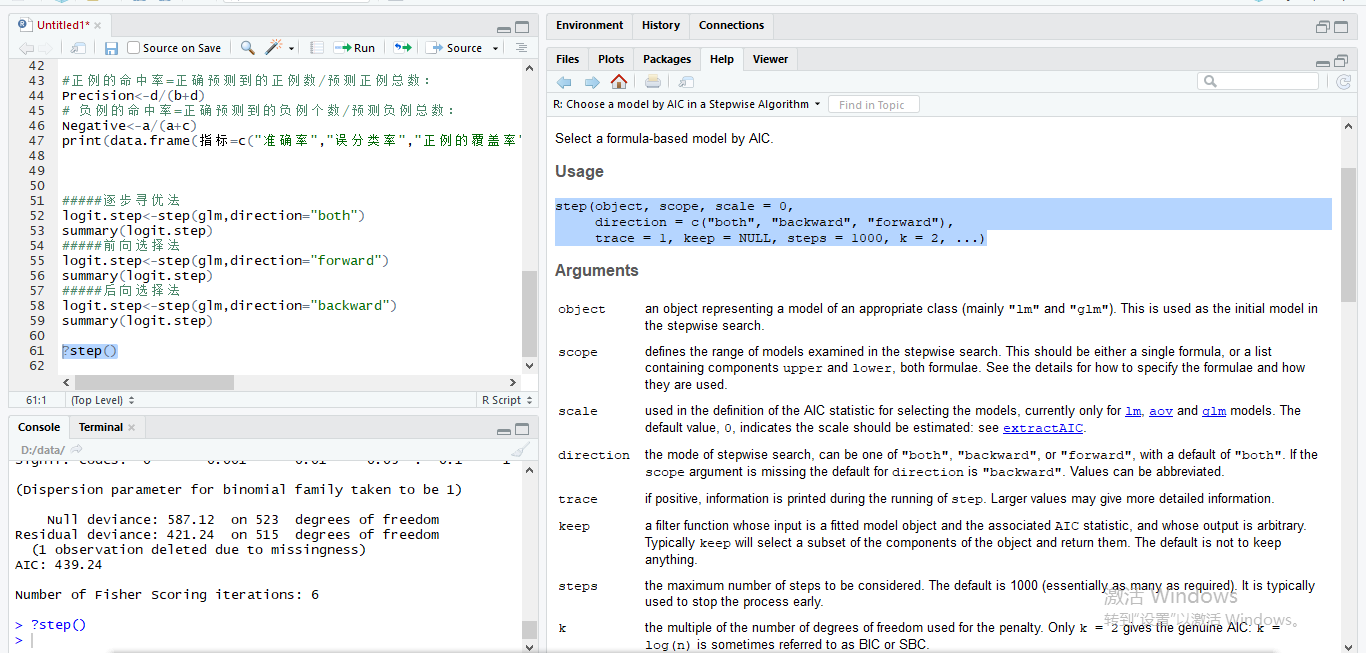
    #####逐步寻优法
    logit.step<-step(glm,direction="both")
    summary(logit.step)
    #####前向选择法
    logit.step<-step(glm,direction="forward")
    summary(logit.step)
    #####后向选择法
    logit.step<-step(glm,direction="backward")
    summary(logit.step)

 

 

    ?step()

 

 

　　看来学好英语还是很重要的Σ(= = !)　　期待中文文档ing!!!