R_Studio(神经网络)BP神经网络算法预测销量的高低

 

 

　　BP神经网络　　百度百科：传送门

　　BP(back propagation)神经网络：一种按照误差逆向传播算法训练的多层前馈神经网络，是目前应用最广泛的神经网络

 

　　

 

#设置文件工作区间
setwd('D:\\dat') 
#读入数据
Gary=read.csv("sales_data.csv")[,2:5]
#数据命名
library(nnet)
colnames(Gary)<-c("x1","x2","x3","y")

###最终模型
model1=nnet(y~.,data=Gary,size=6,decay=5e-4,maxit=1000)  

pred=predict(model1,Gary[,1:3],type="class")    
(P=sum(as.numeric(pred==Gary$y))/nrow(Gary))
table(Gary$y,pred)
prop.table(table(Gary$y,pred),1)

 

 

实现过程

 

　　目的：通过BP神经网络预测销量的高低

 

　　数据预处理，对数据进行重命名并去除无关项

> #设置文件工作区间
> setwd('D:\\dat') 
> #读入数据
> Gary=read.csv("sales_data.csv")[,2:5]
> #数据命名
> library(nnet)
> colnames(Gary)<-c("x1","x2","x3","y")
> Gary
     x1  x2  x3    y
1   bad yes yes high
2   bad yes yes high
3   bad yes yes high
4   bad  no yes high
5   bad yes yes high
6   bad  no yes high
7   bad yes  no high
8  good yes yes high
9  good yes  no high
10 good yes yes high
11 good yes yes high
12 good yes yes high
13 good yes yes high
14  bad yes yes  low
15 good  no yes high
16 good  no yes high
17 good  no yes high
18 good  no yes high
19 good  no  no high
20  bad  no  no  low
21  bad  no yes  low
22  bad  no yes  low
23  bad  no yes  low
24  bad  no  no  low
25  bad yes  no  low
26 good  no yes  low
27 good  no yes  low
28  bad  no  no  low
29  bad  no  no  low
30 good  no  no  low
31  bad yes  no  low
32 good  no yes  low
33 good  no  no  low
34 good  no  no  low

 

　　nnet：包实现了前馈神经网络和多项对数线性模型。前馈神经网络是一种常用的神经网络结构，如下图所示

　　

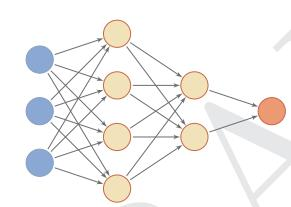
　　前馈网络中各个神经元按接受信息的先后分为不同的组。每一组可以看作一个神经层。每一层中的神经元接受前一层神经元的输出，并输出到下一层神经元。整个网络中的信息是朝一个方向传播，没有反向的信息传播。前馈网络可以用一个有向无环路图表示。前馈网络可以看作一个函数，通过简单非线性函数的多次复合，实现输入空间到输出空间的复杂映射。这种网络结构简单，易于实现。前馈网络包括全连接前馈网络和卷积神经网络等

 

使用neet()方法创建模型

 

　　neet()方法：

　　decay: 权重衰减parameter for weight decay. Default 0.

　　maxit: 最大迭代次数

 

x: 训练样本数据集的输入集合
y: x对应的训练样本数据集的标签（类）集合
weights: 
size: 隐层节点数， Can be zero if there are skip-layer units.
data:训练数据集.
subset: An index vector specifying the cases to be used in the training sample. (NOTE: If given, this argument must be named.)
na.action: A function to specify the action to be taken if NAs are found. The default action is for the procedure to fail. An alternative is na.omit, which leads to rejection of cases with missing values on any required variable. (NOTE: If given, this argument must be named.)
contrasts:a list of contrasts to be used for some or all of the factors appearing as variables in the model formula.
Wts: 边的权重. If missing chosen at random.
mask: logical vector indicating which parameters should be optimized (default all).
linout: 是否为逻辑输出单元，若为FALSE，则为线性输出单元
entropy: switch for entropy (= maximum conditional likelihood) fitting. Default by least-squares.
softmax: switch for softmax (log-linear model) and maximum conditional likelihood fitting. linout, entropy, softmax and censored are mutually exclusive.
censored: A variant on softmax, in which non-zero targets mean possible classes. Thus for softmax a row of (0, 1, 1) means one example each of classes 2 and 3, but for censored it means one example whose class is only known to be 2 or 3.
skip: switch to add skip-layer connections from input to output.
rang: Initial random weights on [-rang, rang]. Value about 0.5 unless the inputs are large, in which case it should be chosen so that rang * max(|x|) is about 1.
decay: 权重衰减parameter for weight decay. Default 0.
maxit: 最大迭代次数
Hess: If true, the Hessian of the measure of fit at the best set of weights found is returned as component Hessian.
trace: switch for tracing optimization. Default TRUE.
MaxNWts: The maximum allowable number of weights. There is no intrinsic limit in the code, but increasing MaxNWts will probably allow fits that are very slow and time-consuming.
abstol: Stop if the fit criterion falls below abstol, indicating an essentially perfect fit.
reltol: Stop if the optimizer is unable to reduce the fit criterion by a factor of at least 1 - reltol.

 

model1=nnet(y~.,data=Gary,size=6,decay=5e-4,maxit=1000)
# weights:  31
initial  value 27.073547 
iter  10 value 16.080731
iter  20 value 15.038060
iter  30 value 14.937127
iter  40 value 14.917485
iter  50 value 14.911531
iter  60 value 14.908678
iter  70 value 14.907836
iter  80 value 14.905234
iter  90 value 14.904499
iter 100 value 14.904028
iter 110 value 14.903688
iter 120 value 14.903480
iter 130 value 14.903450
iter 130 value 14.903450
iter 130 value 14.903450
final  value 14.903450 
converged

 

评估模型

> pred=predict(model1,Gary[,1:3],type="class")
> (P=sum(as.numeric(pred==Gary$y))/nrow(Gary))
[1] 0.7647059
> table(Gary$y,pred)
      pred
       high low
  high   14   4
  low     4  12
> prop.table(table(Gary$y,pred),1)
      pred
            high       low
  high 0.7777778 0.2222222
  low  0.2500000 0.7500000

 

　　得到混淆矩阵图后可以看出

　　检测样本为34个，预测正确的个数为26个，预测准确率为76.5%，预测准确率较低

　　原因：由于神经网络训练时需要较多的样本，而这里训练集比较少