mysql索引原理及优化(二)
2019-08-12 00:19 清风软件测试开发 阅读(363) 评论(0) 收藏 举报索引原理分析:数据结构
索引是最常见的慢查询优化方式
其是一种优化查询的数据结构,MySql中的索引是用B+树实现,而B+树就是一种数据结构,可以优化查询速度,可以利用索引快速查找数据,优化查询。
可以提高查询速度的数据结构:
哈希表、完全平衡二叉树、B树、B+树等等。
哈希:select* from sanguo where name>'周瑜 哈希表的特点是可以快速的精确查询,但是不支持范围查询。
完全平衡二叉树:对于数据量大情况,它相比于哈希或者B树、B+树需要查找次数更多。
B树:比完全平衡二叉树要矮,查询速度更快,所需索引空间更小。
B+树:B+树比B树要胖,B+树的非叶子节点会冗余一份在叶子节点中,并且也在叶子节点会用指针相连。
B树相比完全平衡二叉树查询次数更少,即有更少的磁盘IO次数,性能更优;
B+树是B树的升级版,其为了提高范围查找的效率。
总结:Mysql选用B+树这种数据结构作为索引,可以提高查询索引时的磁盘IO效率,并且可以提高范围查询的效率,并且B+树里的元素也是有序的。
索引的最左前缀原则:当建立多个字段联合索引时,如(a,b,c) 查询条件只会走三类索引 即 a 、 ab 、 abc, ac也走,但是只走a索引。
为什么哈希表、完全平衡二叉树、B树、B+树都可以优化查询,为何Mysql独独喜欢B+树?
哈希表有什么特点?
假如有这么一张表(表名:sanguo):
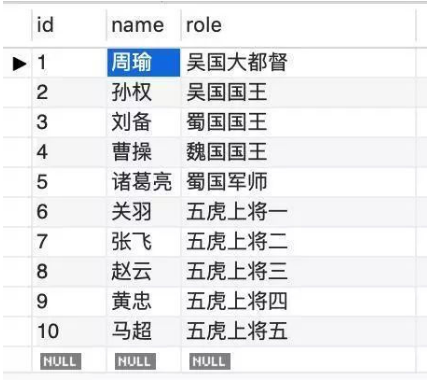
现在对 name 字段建立哈希索引:
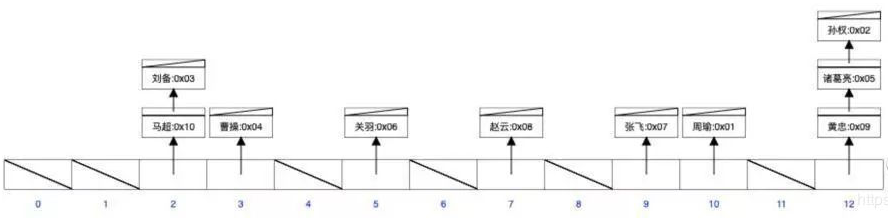
注意字段值所对应的数组下标是哈希算法随机算出来的,所以可能出现哈希冲突。那么对于这样一个索引结构,现在来执行下面的sql语句:
select * from sanguo where name='周瑜'
可以直接对‘周瑜’按哈希算法算出来一个数组下标,然后可以直接从数据中取出数据并拿到所对应那一行数据的地址,进而查询那一行数据。 那么如果现在执行下面的sql语句:
select * from sanguo where name>'周瑜'
则无能为力,因为哈希表的特点就是可以快速的精确查询,但是不支持范围查询。
如果用完全平衡二叉树呢?
还是上面的表数据用完全平衡二叉树表示如下图(为了简单,数据对应的地址就不画在图中了。):
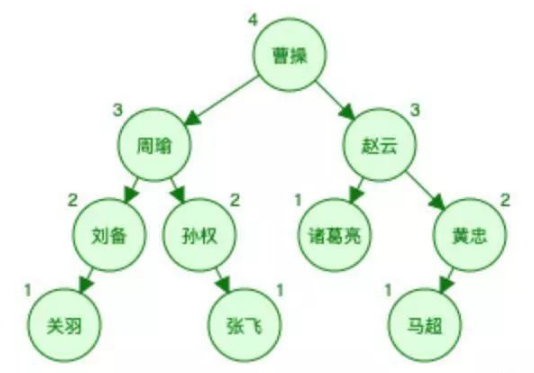
图中的每一个节点实际上应该有四部分:
-
左指针,指向左子树
-
键值
-
键值所对应的数据的存储地址
-
右指针,指向右子树
另外需要提醒的是,二叉树是有顺序的,简单的说就是“左边的小于右边的”假如我们现在来查找‘周瑜’,需要找2次(第一次曹操,第二次周瑜),比哈希表要多一次。
而且由于完全平衡二叉树是有序的,所以也是支持范围查找的。
如果用B树呢?
还是上面的表数据用B树表示如下图(为了简单,数据对应的地址就不画在图中了。):
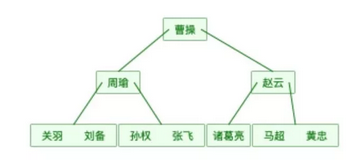
可以发现同样的元素,B树的表示要比完全平衡二叉树要“矮”,原因在于B树中的一个节点可以存储多个元素。
如果用B+树呢?
还是上面的表数据用B+树表示如下图(为了简单,数据对应的地址就不画在图中了。):
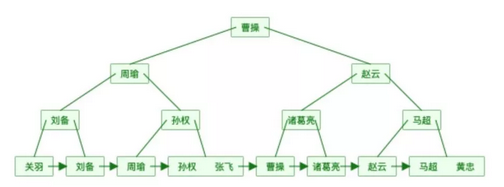
我们可以发现同样的元素,B+树的表示要比B树要“胖”,原因在于B+树中的非叶子节点会冗余一份在叶子节点中,并且叶子节点之间用指针相连。
那么B+树到底有什么优势呢?
这里我们用“反证法”,假如我们现在就用完全平衡二叉树作为索引的数据结构,我们来看一下有什么不妥的地方。实际上,索引也是很“大”的,因为索引也是存储元素的,我们的一个表的数据行数越多,那么对应的索引文件其实也是会很大的,实际上也是需要存储在磁盘中的,而不能全部都放在内存中,所以我们在考虑选用哪种数据结构时,我们可以换一个角度思考,哪个数据结构更适合从磁盘中读取数据,或者哪个数据结构能够提高磁盘的IO效率。回头看一下完全平衡二叉树,当我们需要查询“张飞”时,需要以下步骤:
-
从磁盘中取出“曹操”到内存,CPU从内存取出数据进行比较,“张飞”<“曹操”,取左子树(产生了一次磁盘IO)
-
从磁盘中取出“周瑜”到内存,CPU从内存取出数据进行比较,“张飞”>“周瑜”,取右子树(产生了一次磁盘IO)
-
从磁盘中取出“孙权”到内存,CPU从内存取出数据进行比较,“张飞”>“孙权”,取右子树(产生了一次磁盘IO)
-
从磁盘中取出“黄忠”到内存,CPU从内存取出数据进行比较,“张飞”=“张飞”,找到结果(产生了一次磁盘IO)
从上面可以发现:完全平衡二叉树,当我们需要查询“张飞”时需要4次磁盘IO,也就是4次从磁盘中取出数据(磁盘块)到内存
同理,回头看一下B树,我们发现只发送三次磁盘IO就可以找到“张飞”了,这就是B树的优点:一个节点可以存储多个元素,相对于完全平衡二叉树所以整棵树的高度就降低了,磁盘IO效率提高了。
而B+树是B树的升级版,只是把非叶子节点冗余一下,这么做的好处是为了提高范围查找的效率。
Mysql中MyISAM和innodb 的B+树结构如下图:
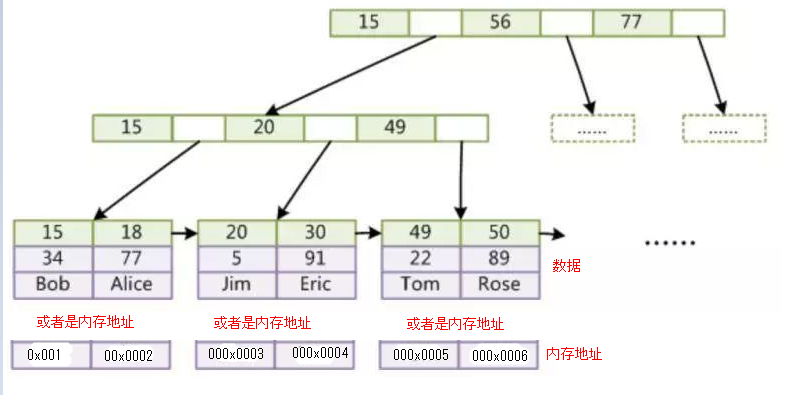
通常我们认为B+树的非叶子节点不存储数据,只有叶子节点才存储数据;而B树的非叶子和叶子节点都会存储数据,会导致非叶子节点存储的索引值会更少,树的高度相对会比B+树高,平均的I/O效率会比较低,所以使用B+树作为索引的数据结构,再加上B+树的叶子节点之间会有指针相连,也方便进行范围查找。上图的data区域两个存储引擎会有不同。
那么,一个B+树的节点中到底存多少个元素合适呢?
其实也可以换个角度来思考B+树中一个节点到底多大合适?
答案是:B+树中一个节点为一页或页的倍数最为合适。因为如果一个节点的大小小于1页,那么读取这个节点的时候其实也会读出1页,造成资源的浪费;如果一个节点的大小大于1页,比如1.2页,那么读取这个节点的时候会读出2页,也会造成资源的浪费;所以为了不造成浪费,所以最后把一个节点的大小控制在1页、2页、3页、4页等倍数页大小最为合适。
那么,Mysql中B+树的一个节点大小为多大呢?
这个问题的答案是“1页”,这里说的“页”是Mysql自定义的单位(其实和操作系统类似),Mysql的Innodb引擎中一页的默认大小是16k(如果操作系统中一页大小是4k,那么Mysql中1页=操作系统中4页),可以使用命令SHOW GLOBAL STATUS like 'Innodb_page_size'; 查看。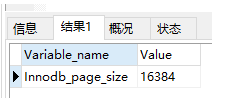
对着上面Mysql中Innodb中对B+树的实际应用(主要看主键索引),可以发现B+树中的一个节点存储的内容是:
非叶子节点:主键+指针
叶子节点:数据
那么,假设我们一行数据大小为1K,那么一页就能存16条数据,也就是一个叶子节点能存16条数据;再看非叶子节点,假设主键ID为bigint类型,那么长度为8B,指针大小在Innodb源码中为6B,一共就是14B,那么一页里就可以存储16K/14=1170个(主键+指针),那么一颗高度为2的B+树能存储的数据为:117016=18720条,一颗高度为3的B+树能存储的数据为:11701170*16=21902400(千万级条)。所以在InnoDB中B+树高度一般为1-3层,它就能满足千万级的数据存储。在查找数据时一次页的查找代表一次IO,所以通过主键索引查询通常只需要1-3次IO操作即可查找到数据。所以也就回答了我们的问题,1页=16k这么设置是比较合适的,是适用大多数的企业的,当然这个值是可以修改的,所以也能根据业务的时间情况进行调整。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号