第八章

8.4
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

def system(z,t):
x,y=z
dxdt=-x3-y
dydt=x-y3

return [dxdt,dydt]

z0=[1,0.5]
t = np.linspace(0, 30, 1000)

sol=odeint(system,z0,t)

x_sol=sol[:,0]
y_sol=sol[:,1]

plt.subplot(2, 1, 1)
plt.plot(t, x_sol)
plt.xlabel('t')
plt.ylabel('x(t)')
plt.title('Solution of x(t)')

plt.subplot(2, 1, 2)
plt.plot(t, y_sol)
plt.xlabel('t')
plt.ylabel('y(t)')
plt.title('Solution of y(t)')

plt.tight_layout()
plt.show()

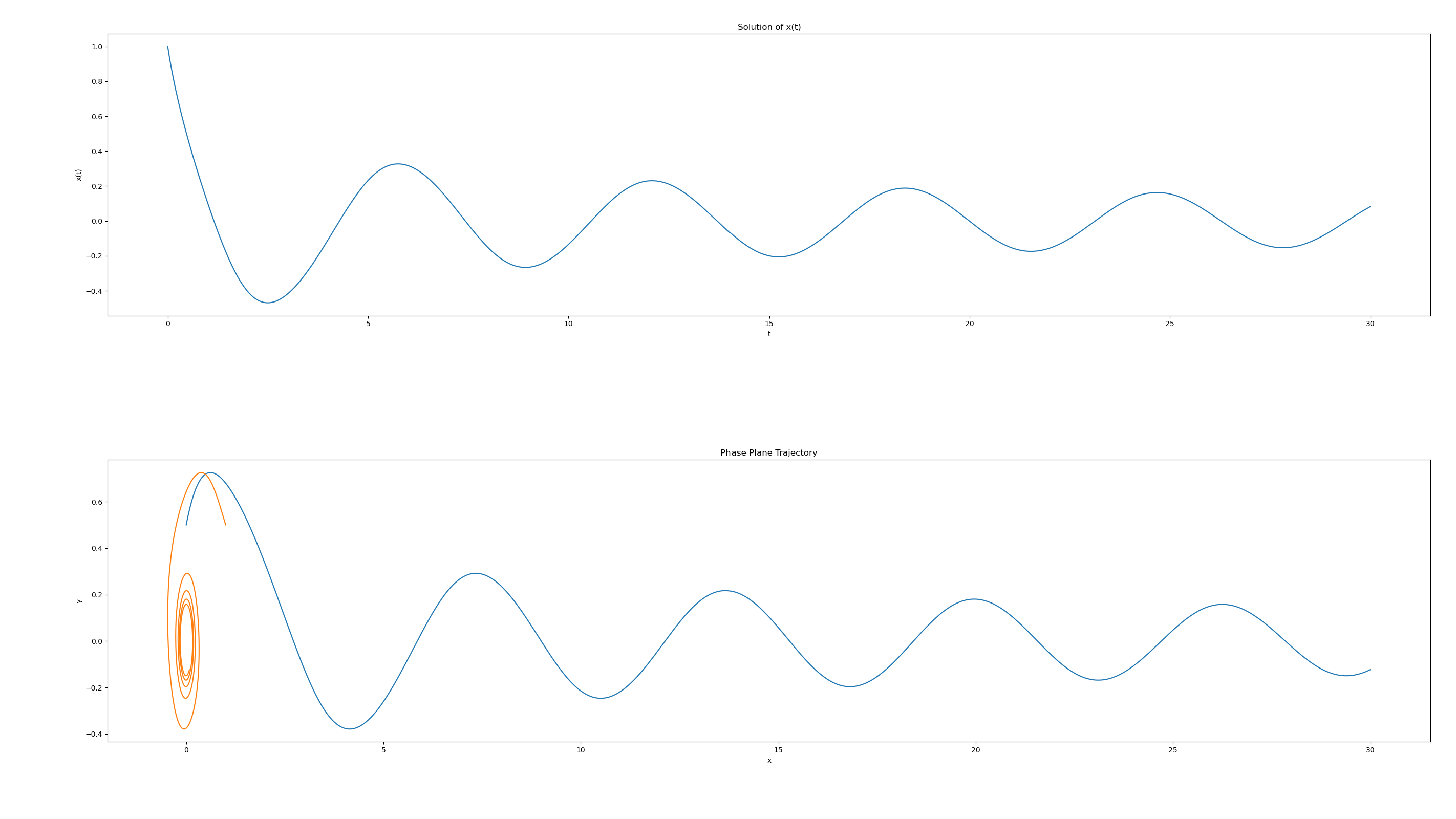
plt.plot(x_sol, y_sol)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Phase Plane Trajectory')
plt.show()
print("3023")
结果

8.5
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

plt.rcParams['text.usetex'] = False

def model(t, y):
f, df_dm, d2f_dm2, T, dT_dm = y
d3f_dm3 = -3 * f * d2f_dm2 + 2 * (df_dm) ** 2 - T
d2T_dm2 = -2.1 * f * dT_dm
return [df_dm, d2f_dm2, d3f_dm3, dT_dm, d2T_dm2]

y0 = [0, 0, 0.68, 1, -0.5]

t_span = (0, 10)
t_eval = np.linspace(t_span[0], t_span[1], 1000)

try:
sol = solve_ivp(model, t_span, y0, t_eval=t_eval, method='RK45')
if not sol.success:
raise ValueError(f"求解微分方程组失败: {sol.message}")
except Exception as e:
print(f"发生错误: {e}")
exit(1)

f = sol.y[0]
T = sol.y[3]

plt.figure(figsize=(12, 6))

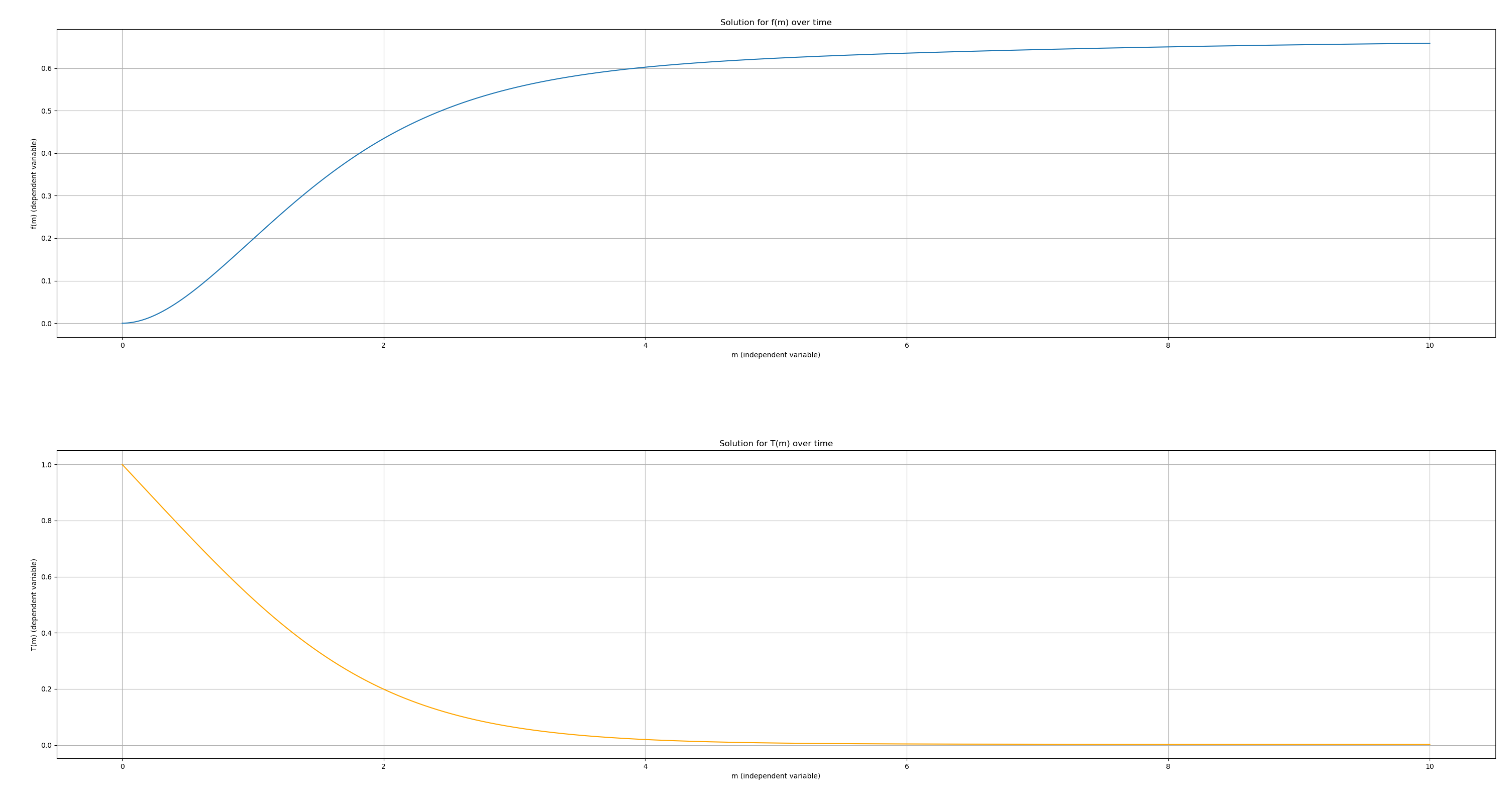
plt.subplot(2, 1, 1)
plt.plot(sol.t, f, label='f(m)')
plt.xlabel('m (independent variable)')
plt.ylabel('f(m) (dependent variable)')
plt.title('Solution for f(m) over time')
plt.grid(True)

plt.subplot(2, 1, 2)
plt.plot(sol.t, T, label='T(m)', color='orange')
plt.xlabel('m (independent variable)')
plt.ylabel('T(m) (dependent variable)')
plt.title('Solution for T(m) over time')
plt.grid(True)

plt.tight_layout()
plt.show()
print("3023")
结果

8.8
loan_principal = (600000 - 200000)

monthly_interest_rate = 0.0036

total_months = 30 * 12

monthly_payment = (loan_principal * monthly_interest_rate * (1 + monthly_interest_rate) ** total_months) / ((1 + monthly_interest_rate) ** total_months - 1)
print("等额还款时月还款额为：{:.2f}元".format(monthly_payment))
print("3023")
结果

8.9
import numpy as np
import matplotlib.pyplot as plt

a = 1 - 0.2 * (1 / 12)
m = 1.109 * 10 ** 5
w3 = 17.86
w4 = 22.99

X = []
Z = []

for k in np.arange(0, 0.875, 0.001):

x1 = 1.221011 * (1 - 1 / (m * (1 - a - 0.42 * k) ** 8 * (1 - a) ** 24 * (0.5 + (1 - a - k) ** 8 * (1 - a) ** 4)))


x2 = (1 - a) ** 12 * x1


x3 = (1 - a) ** 12 * x2


x4 = (1 - a - 0.42 * k) ** 8 * (1 - a) ** 4 * x3


X.append([x1, x2, x3, x4])


z = (0.42 * k * w3 * (1 - (1 - a - 0.42 * k) ** 8) / (a + 0.42 * k) * x3 +
     k * w4 * (1 - (1 - a - k) ** 8) / (a + k) * x4)
Z.append(z)

mz = max(Z)
ind = Z.index(mz)

print('最大生产量：', mz)
print('各年龄组鱼群数（在最大生产量对应的 k 值下）：', X[ind])
print('对应的 k 值（用于索引计算，可能需要根据实际情况转换为实际 k 值）：', ind * 0.001)

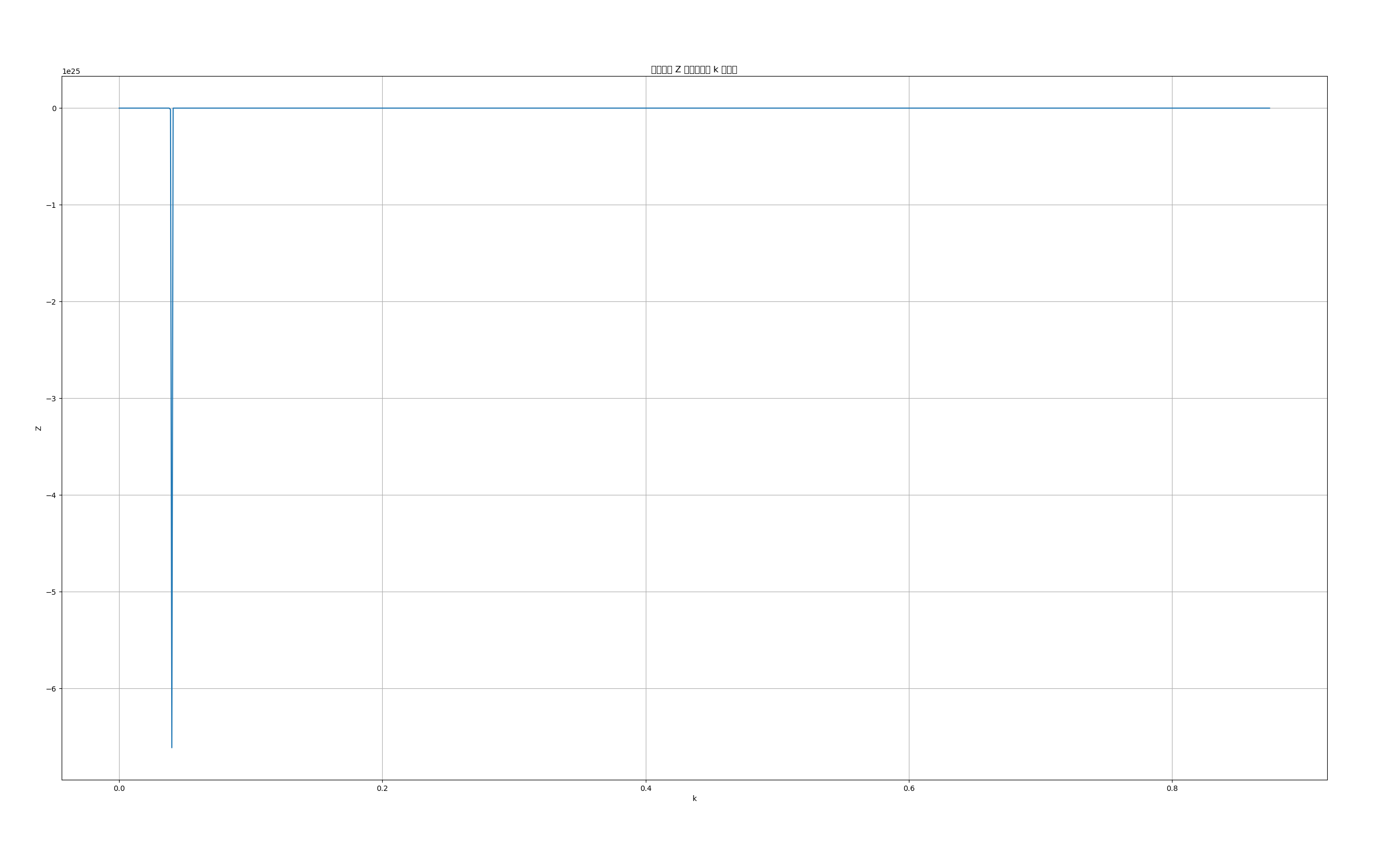
plt.plot(np.arange(0, 0.875, 0.001), Z)
plt.ylabel('Z')
plt.xlabel('k')
plt.title('总生产量 Z 随捕捞强度 k 的变化')
plt.grid(True)
plt.show()
print("3023")
结果