匀速圆周运动向心加速度推导
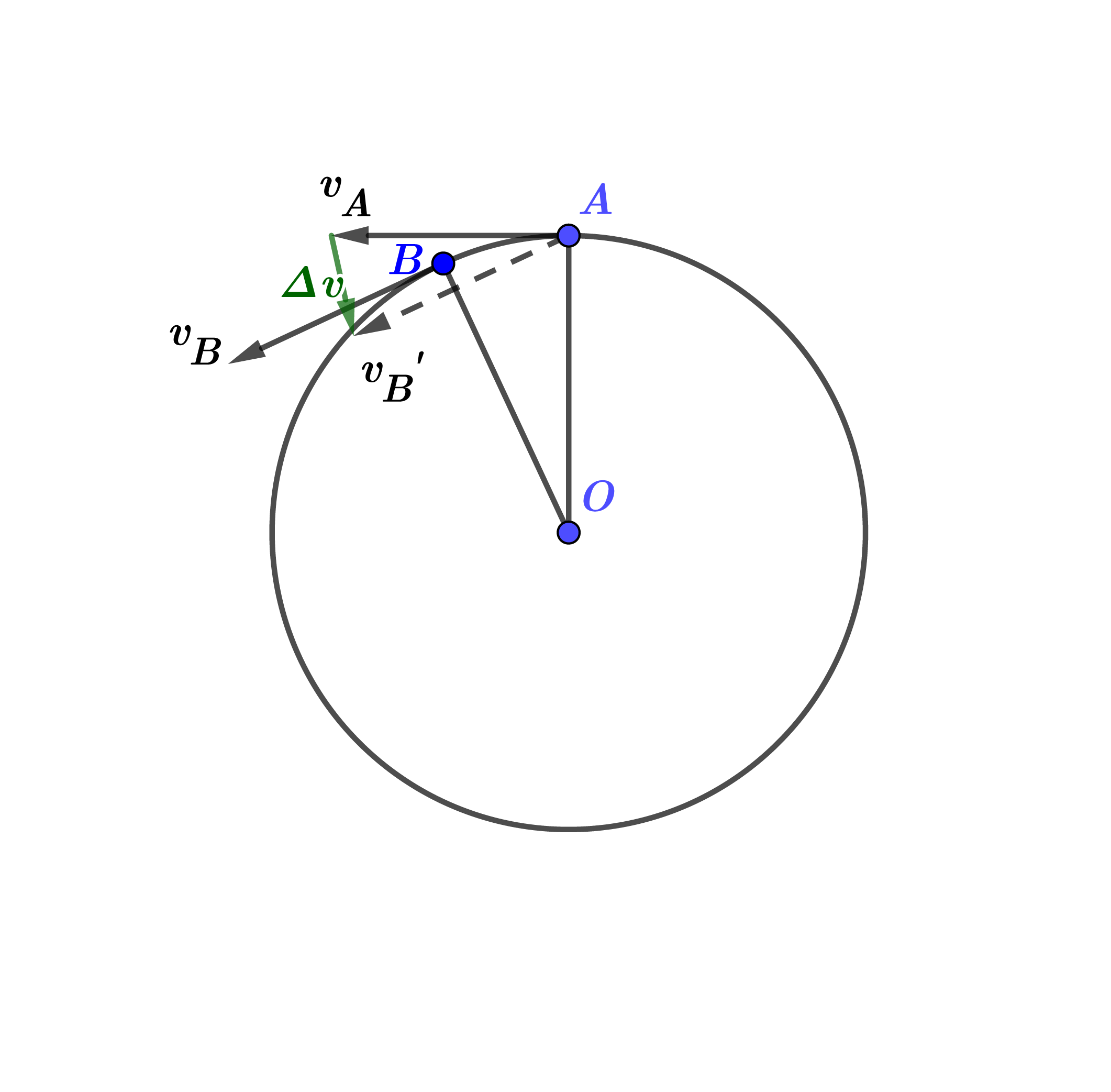
某时刻质点位于\(A\)点，速度为\(v_A\)。经过\(\Delta t\)时间，运动到\(B\)点。
把\(v_B\)矢量的始端移至\(A\)点（\(v_B'\)），速度改变量\(\Delta v=v_B-v_A\)。
速度\(v_A,v_B',\Delta v\)围成的三角形与\(\triangle OAB\)相似，则
\[\Delta v=\Delta s\frac{v}{r}
\]
同除以\(\Delta t\)得
\[\frac{\Delta v}{\Delta t}=\frac{\Delta s}{\Delta t} \cdot \frac{v}{r}
\]
当\(\Delta t\)趋近于零时，\(\frac{\Delta v}{\Delta t}\)表示向心加速度\(a\)的大小，\(\frac{\Delta s}{\Delta t}\)表示线速度的大小\(v\)。
于是得到
\[a=\frac{v^2}{r}
\]
