UnicodeMath编码教程

参考UnicodeMath官方文档，原文看这。
word插入公式不自动斜体的解决办法
建议先看：微软官网Word 中使用 UnicodeMath 和 LaTeX 的线性格式公式
本文持续更新。

目录

• 1. 简介
• 2. 编码简单数学表达式
  • 2.1 分数
  • 2.3 空白（空格）字符使用
• 3. 编码其他数学公式
  • 3.1 open/close分隔符
    • 关于大括号方程组（cases）
    • 关于缩放
    • 关于绝对值
  • 3.2 转义
  • 3.3 向上/向下操作符
  • 3.4 第三个参数（n-aryand）
• 4. 输入方法

1. 简介

用UnicodeMath写数学表达式很简单，而且编码非常易读，比较接近手写的数学表达式。因此这种编码叫做“近纯文本格式”。

后文中近纯文本格式称为 线性格式 ，将构建的表示格式称为 构建格式。

线性格式比[La]TeX或MathML更紧凑、易读。来个对比：

公式：\(\frac{(a+c)}{d}\)

线性格式：((a+c))/d

[La]Tex：$\frac{(a+c)}{d}$

MathML：

<mfrac>
    <mrow>
        <mi>a</mi>
        <mo>+</mo>
        <mi>c</mi>
    </mrow>
    <mi>d</mi>
</mfrac>

大多数数学表达式可以用线性格式明确表示，线性格式也可导出为[La]TeX、MathML格式。线性格式借用了部分TeX的符号，用来表示自己表示不了的东西，例如矩阵。

提示：后文中或将出现许多键盘上没有的Unicode符号，但它们大都可以用word的数学符号自动更正输入。你可以查看word的所有数学符号自动更正：

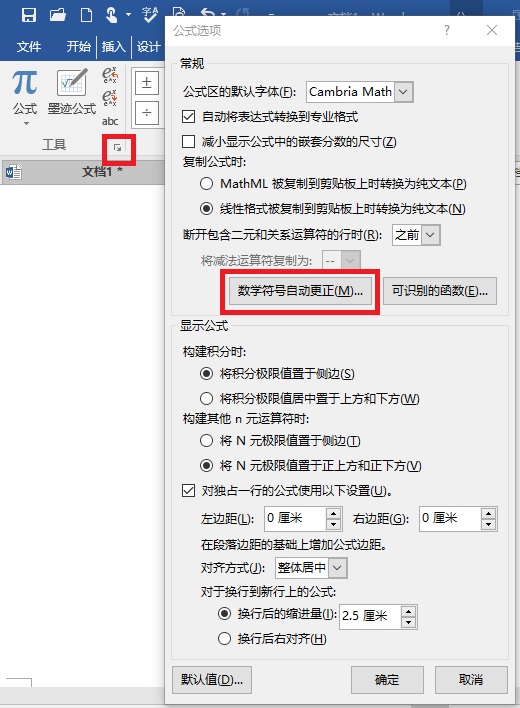
部分自动更正附在文后的自动更正列表

2. 编码简单数学表达式

2.1 分数

表示分数可以用LaTeX的\frac{numerator} {denominator}。

在线性格式中：输入a/b，再敲个空格，完事。比Tex快多了。

给几个例子：

\[\frac{abc}{d}$$ 线性格式是`abc/d`。要强制显示正常大小的线性分数（横着写），可以使用`\ /`（反斜杠后跟斜杠）。 线性格式`(a+c)/d`显示为$\frac{a+b}{d}$。 那问题来了，怎么才能输入$\frac{(a+b)}{d}$？很简单，再打一对括号：`((a+b))/d` 另外，分数线样式有三种： 1. “分数斜线”U+2044（可以通过`\sdiv`输入） 1. “除法斜线”U+2215（`\ldiv`） 1. 带圆圈的斜线（U+2298,`\ndiv`） 三种分别显示成  **提示**：由于分数线`/`后面不可能跟着运算符，所以`/`号被定义为取反，即键入`/=`就可得到`≠`（类似编程语言中的`!=`）。类似的有： | Operator | Negated op | Input | |----------|------------|--------------| | < | ≮ | /< | | = | ≠ | /= | | > | ≯ | /> | | ∃ | ∄ | /\exists | | ∈ | ∉ | /\in | | ∋ | ∌ | /\ni | | ∼ | ≁ | /\sim | | ≃ | ≄ | /\simeq | | ≅ | ≇ | /\cong | | ≈ | ≉ | /\approx | | ≍ | ≭ | /\asymp | | ≡ | ≢ | /\equiv | | ≤ | ≰ | /\le | | ≥ | ≱ | /\ge | | ≶ | ≸ | /\lessgtr | | ≷ | ≹ | /\gtrless | | ≽ | ⋡ | /\succeq | | ≺ | ⊀ | /\prec | | ≻ | ⊁ | /\succ | | ≼ | ⋠ | /\preceq | | ⊂ | ⊄ | /\subset | | ⊃ | ⊅ | /\supset | | ⊆ | ⊈ | /\subseteq | | ⊇ | ⊉ | /\supseteq | | ⊑ | ⋢ | /\sqsubseteq | | ⊒ | ⋣ | /\sqsupseteq | 分数的另一个技巧是两个数字之间或斜杠和数字之间的句点或逗号被认为是数字的一部分，而不是终结符。例如，`1/3.1416`为 $\frac{1}{3.1416}$，而不是$\frac{1}{3}.1416$。 ## 2.2 上标和下标 `_`实现下标：$\delta_{\mu\nu}$ 写为`δ_μν`。 类似地，`^`实现上标。所以 `a^b` 表示 $a^b$ 。 复杂一点，加个括号： $\delta_{\mu+\nu}$ 写为`δ_(μ+ν)`。 上/下标的嵌套：`a_b_c`代表$a_{b_c}$。类似地，`a^b^c` 代表$a^{b^c}$。 $a^{b_c}$ 写为`a^(b_c)`，而不是`a^b_c`。因为`a^b_c`(或`a_c^b`)显示为$a^b_c$。 稍微复杂的例子，想想这个表达式怎么写？ $W^{3\beta}_{\delta_1\rho_2\sigma_3}$ 其线性格式为`W^(3β)_(δ_1ρ_1σ_2)`。而在TeX中，需要这样输入 `$W^{3\beta}_{\delta_1\rho_1\sigma_2}$` 对于 $$\alpha_2^3\over\beta_2^3+ \gamma_2^3\]

线性格式文本可以为α_2^3/(β_2^3+γ_2^3)，而标准的TeX版本为$$\alpha_2^3 \over \beta_2^3 + \gamma_2^3$$。

更长的：

\[W_{\delta_1\rho_1\sigma_2}^{3\beta}= U_{\delta_1\rho_1}^{3\beta}+ {1 \over 8\pi^2} \int_{\alpha_1}^{\alpha_2} d\alpha_2’ \left[ {U_{\delta_1\rho_1}^{2\beta}-\alpha_2’ U_{\rho_1\sigma_2}^{1\beta}\over U_{\rho_1\sigma_2}^{0\beta}} \right] \]

它的线性格式版本为
W_(δ1ρ1σ2)^(3β)=U_(δ1ρ1)^(3β)+1/8π^2 ∫_α1^α2▒dα'_2 [(U_(δ1ρ1)^(2β)-α'_2U_(ρ1σ2)^(1β))/U_(ρ1σ2)^(0β)]
而标准的TeX版本为

$$W_{\delta_1\rho_1\sigma_2}^{3\beta}=
 U_{\delta_1\rho_1}^{3\beta}+ {1 \over 8\pi^2}
 \int_{\alpha_1}^{\alpha_2} d\alpha_2’ \left[
     {U_{\delta_1\rho_1}^{2\beta}-\alpha_2’
     U_{\rho_1\sigma_2}^{1\beta}\over
     U_{\rho_1\sigma_2}^{0\beta}} \right] $$

2.3 空白（空格）字符使用

输入\alpha跟一个空格将获得α，当α替换\alpha时，空格被消除。类似地，a_1 b_2 会显示\(a_1b_2\)（中间没有空格）。

空格可以理解为局部写完了，进行提交。推荐一篇在Word中使用UnicodeMath和Latex优雅地输入线性公式对空格的叙述比较详细。
补充：x=(-b\pm<space>\sqrt(b^2-4ac))/(2a)<space>输入时在这两处空格。

在嵌套的下标/上标表达式中，空格一次构建一个上/下标。例如，要用编码a^b^c建立\(a^{b^c}\)，需要两个空格。

像+这样的其他运算符会构建整个表达式，因为这些运算符明确地终止了操作。

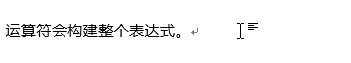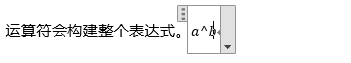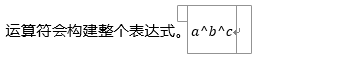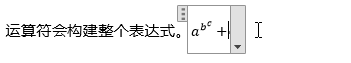
3. 编码其他数学公式

3.1 open/close分隔符

├(\open)和┤(\close)用于标志分隔（类似LaTeX的“\begin” “\end”）。

关于\open \close:4.6 线性格式自动更正列表

关于大括号方程组（cases）

分段函数
\(\left|x\right|=\begin{cases}x & x \geq 0\\-x & x < 0\end{cases}\)
的线性格式为：|x|={█(x &x≥0@-x &x<0)┤

关于操作符“ █ ”见3.19 方程组

补充：输入大括号括起来的方程组，还可以先输入\close，后输入方程组内容：

也可使用“&”进行对齐：

由于cases（分类讨论）很常见，线性格式v3中将符号“ Ⓒ ”(\cases)定义为cases的标志（类似于Tex的{cases}环境）。上面的编码等效于：|x|=Ⓒ(x &x≥0@-x &x<0)

也就是说，{█和┤(\close)可以用一个Ⓒ(\cases)替代。

关于缩放

UnicodeMath提供了类似于LaTeX\big \Big \bigg \Bigg的对符号进行放大的用法。

Latex代码：

\Bigg\{
  \bigg\{
    \Big[
      \big(
       (x)
     \big)
    \Big]
  \bigg\}
\Bigg\}

效果：

\[\Bigg\{ \bigg\{ \Big[ \big( (x) \big) \Big] \bigg\} \Bigg\} \]

UnicodeMath编码：在├后加一个数字‘0’-‘4’，代表放大值。对照表：

Digit	Meaning
0	Don't grow
1	big
2	Big
3	bigg
4	Bigg

因此上面例子线性格式为：
├4{├3{├2[├1(├0(x))]}}

但实际上，如果不是必须，不建议使用这种办法。因为不说明大小，程序也会自动进行放大。

关于绝对值

UnicodeMath中绝对值直接用竖杆“|”(U+007C)表示（LaTeX是\left| \right|），按空格构建。

然而，如何输入\(\big| \left| x \right| - \left| y \right| \big|\)?

如果直接输入||x|-|y||，结果将会是\(\left|\right|x\left|-\right|y\left|\right|\).

正确的线性格式为：|(|x|-|y|)|

从中我们了解到，不指明层级（使用括号）时，默认竖杆|与其后跟的第一个|为一对绝对值。

3.2 转义

如果你想把UnicodeMath中某个“关键字”当作普通文本识别的话，在他前面加反斜杠\。

例如，\[将显示为原原本本的方括号，程序不会为它匹配]。

3.3 向上/向下操作符

线性格式(_c^b)a或_c^a b显示为\({_c^b}a\)。

线性格式lim┬(n→∞)a_n显示为\(\lim_{n \rightarrow 0}{a_n}\)。

\above(┴)\below(┬)表示上下标。

3.4 第三个参数（n-aryand）

像积分、求和、极限这样的运算符含有上/下标（\above \below ^ _），同时还含有第三个参数（n-aryand）。对于积分，n-aryand是被积函数，对于求和，它是加数。为了识别，符号“▒”(U+2592)作为链接n-aryand的“胶水”。

线性格式∫_0^a▒xⅆx/(x^2+a^2)显示为$$\int_{0}^{{a}\frac{x,dx}{x}2+a^2}$$

中间的“ⅆ”（双线斜体小写d）在word中可用\dd输入。注意这个“ⅆ”在显示时前面有一个小空格（而直接打字母d就不会有这个效果）。

其实在word中打\int会自动匹配第三个参数（显示成虚框）。这个“胶水”了解就好。

3.19 方程组

操作符“ █ ”(\eqarray)使一个方程相对于另一个方程垂直对齐。“&”符号标志对齐位置。
例如：

\[\begin{eqnarray*}10&x+&3&y=2\\ 3&x+&13&y=4\end{eqnarray*} \]

线性格式：
█(10&x+&3&y=2@3&x+&13&y=4)

4. 输入方法

4.6 线性格式自动更正列表

输入"word"再空格，将替换为"Control"。

Control	word	Character	Control	word	Character
\int	∫	(U+222B)	\underbrace	︸	(U+23DF)
\oint	∮	(U+222E)	\overbrace	︷	(U+23DE)
\sum	∑	(U+2211)	\begin	〖	(U+3016)
\prod	∏	(U+220F)	\end	〗	(U+3017)
\funcapply		(U+2061)	\phantom	⟡	(U+27E1)
\naryand,\of	▒	(U+2592)	\box	□	(U+25A1)
\rect	▭	(U+25AD)	\hphantom	⬉	(U+2B04)
\sqrt	√	(U+221A)	\vphantom	⇳	(U+21F3)
\open	├	(U+251C)	\asmash	⬆	(U+2B06)
\close	┤	(U+2524)	\dsmash	⬇	(U+2B07)
\above	┴	(U+2534)	\hsmash	⬌	(U+2B0C)
\below	┬	(U+252C)	\smash	⬈	(U+2B0D)
\underbar	▁	(U+2581)	\matrix	■	(U+25A0)
\overbar	̄	(U+00AF)	\eqarray	█	(U+2588)