FFT

\(\text{Fast Fourier Transformation}\)（快速傅里叶变换），用来加速多项式乘法。朴素算法的时间复杂度：\(O(n^2)\)，而 \(\text{FFT}\) 则为 \(n\log n\)。

多项式的系数表示法和点值表示法

\(\text{FFT}\) 其实是一个用 \(O(n\log_2n)\) 的时间将一个用系数表示的多项式转换成它的点值表示的算法。

系数表示法

一个 \(n\) 次的多项式 \(f(x)\) 可以表示为:

\[f(x)=\sum_{i=0}^{n}{a_ix^i} \]

即可以用每一项的系数来表示 \(f(x)\)：

\[f(x)=\{a_0,a_1,\dots,a_{n-1},a_{n} \} \]

点值表示法

点值表示法是把这个多项式看成一个函数，放在平面直角坐标系中，从上面选取 \(n+1\) 个点，那么这 \(n+1\) 个点就可以唯一确定该多项式，也就是有且仅有一个多项式满足：\(\forall k,f(x_k)=y_k\)，从而利用这 \(n+1\) 个点来唯一地表示这个函数。因为，将这 \(n+1\) 个点的坐标代入，可以得到一个\(n+1\) 条 \(n+1\) 元的线性方程组，有唯一解。

即：

\[f(x)=\{(x_0,f(x_0)),(x_1,f(x_1)),\dots,(x_n,f(x_n)) \} \]

通俗地说，多项式由系数表示法转为点值表示法的过程，就是 \(\text{DFT}\) 的过程。相对地，把一个多项式的点值表示法转化为系数表示法的过程，就是 \(\text{IDFT}\)。而 \(\text{FFT}\) 就是通过取某些特殊的 \(x\) 的点值来加速 \(\text{DFT}\) 和 \(\text{IDFT}\) 的过程。

对于用系数表示的两个多项式，相乘的复杂度为：\(O(n^2)\)，而用点值表示的多项式相乘则需要 \(O(n)\)。

假设两个多项式的点值表示如下：

\[f(x)=\{(x_0,f(x_0)),(x_1,f(x_1)),\dots,(x_n,f(x_n)) \}\\ g(x)=\{(x_0,g(x_0)),(x_1,g(x_1)),\dots,(x_n,g(x_n)) \}\\ \]

若它们的乘积为 \(h(x)\)，则：

\[h(x)=\{(x_0,f(x_0)\times g(x_0)),(x_1,f(x_1)\times g(x_1)),\dots,(x_n,f(x_n)\times g(x_n)) \} \]

目测复杂度为 \(O(n)\)。

但是朴素的系数表示法转点值表示法的算法还是 \(O(n^2)\) 的，逆过程也是如此，即 \(\text{DFT}\) 和 \(\text{IDFT}\)。

复数

对于任意系数多项式转点值，当然可以取任意 \(n\) 个 \(x\) 值代入计算，但是暴力计算 \(x_k^0,x_k^1,\cdots,x_k^{n-1}\) 的复杂度还是 \(O(n^2)\) 的。可以代入一组特殊的 \(x\) ，用来简化计算。因此，我们不要去算 \(x^i\)，可以发现 \(-1\) 和 \(1\) 的幂很好算，但是只有两个完全不够，至少需要 \(n\) 个，使得 \(x\) 的若干次方等于 \(\pm1\)。联系到虚数，长度为 \(1\) 的虚数，不管怎么乘，长度都是 \(1\)，即下图圆（以原点为圆心，\(1\) 为半径的单位圆）上的点均满足要求。

同时，在此处要求 \(n\) 为 \(2\) 的次幂，且要把圆进行 \(n\) 等分。

复数的运算

设两个复数：\(z_1=a+bi,z_2=c+di\)，

则：

\[z_1+z_2=(a+c)+(b+d)i\\ z_1-z_2=(a-c)+(b-d)i\\ z_1\times z_2=(ac-bd)+(ad+bc)i \]

复数相加满足平行四边形法则。

复数相乘的小性质：

\[(\alpha_1,\theta_1)*(\alpha_2,\theta_2)=(\alpha_1\alpha_2,\theta_1+\theta_2) \]

即模长相乘，极角相加。

复根

我们称 \(x^n=1\) 在复数意义下的解是 \(n\) 次单位复根，显然这样的解有 \(n\) 个。设 \(\omega_n^k=e^{\frac{2\pi ki}{n}}\)，则 \(x^n=1\) 的解集为 \(\{\omega_n^k|k=0,1,\cdots,n-1 \}\)。根据复平面的知识，\(n\) 次单位复根是复平面把单位圆 \(n\) 等分的第一个角所对应的向量。其他复根均可以用单位复根的幂表示。

同时，根据欧拉公式，有：

\[\omega_n=e^{\frac{2\pi i}{n}}=\cos\left(\frac{2\pi}{n} \right)+i·\sin\left(\frac{2\pi}{n} \right) \]

如下图中，\(n=4\) 时，\(\omega_n=i\) 就是 \(4\) 次单位复根。

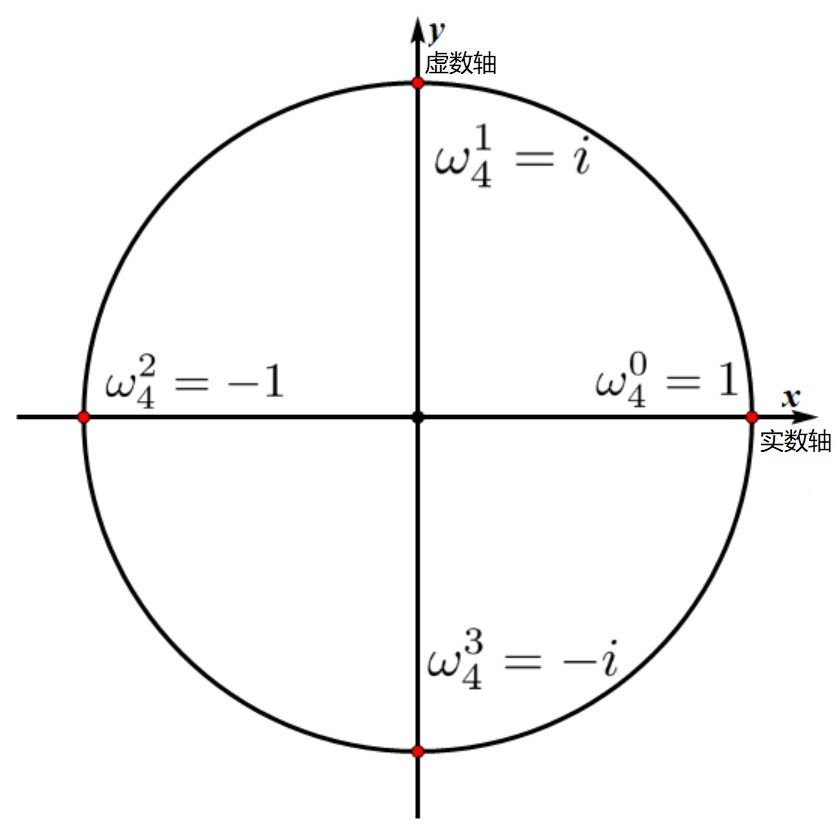
将圆上的点从 \((1,0)\) 开始逆时针进行编号（从 \(0\) 开始），记编号为 \(k\) 的点代表的复数值为 \(\omega_n^k\)，根据复数相乘的性质，有：

\[(\omega^1_n)^k=\omega^k_n \]

其中，\(\omega^1_n\) 称为 \(n\) 次单位复根，而且每一个 \(\omega\) 都可以求出（欧拉公式）。

\[\omega^k_n=\cos\left(\frac{k}{n}2\pi\right)+i· \sin\left(\frac{k}{n}2\pi\right) \]

那么，\(\omega_n^0,\omega_n^1,\omega_n^2,\dots,\omega_n^{n-1}\) 就是要代入 \(x_0,x_1,x_2,\dots ,x_{n-1}\) 的值。

单位复根的性质

• \(\omega_n^k=\omega_{2n}^{2k}\)

• \(\omega_n^{k+\frac{n}{2}}=-\omega_n^k\)

• \(\omega_n^0=\omega_n^n=1\)

上述性质结合图理解应该很好理解，证明的话要利用上面的 \(\omega_n^k\) 的公式。

以上，我们只是对 \(x_i\) 取了一些特殊的值，但最后由 \(h(x)\) 的点表示法求系数表示法时，还是要将值代入 \(O(n^2)\) 去算。

分治

利用分治来进行 \(\text{DFT}\) ，就得到了 \(\text{FFT}\)。

设多项式 \(A(x)\) （\(n\) 为偶数）:

\[A(x)=\sum_{i=0}^{n-1}{a_ix^i}=a_0+a_1x+a_2x^2+\dots+a_{n-1}x^{n-1} \]

按幂的奇偶来将多项式划分为两部分，然后右边提出一个 \(x\)：

\[f(x)=(a_0+a_2x^2+a_4x^4+\dots+a_{n-2}x^{n-2})+x(a_1+a_3x^2+a_5x^4+\dots+a_{n-1}x^{n-2}) \]

可以发现，两边很相似，可以再设两个多项式：\(A_1(x),A_2(x)\)，有：

\[A_1(x)=a_0+a_2x+a_4x^2+\dots+a_{n-2}x^{\frac{n-2}{2}}\\ A_2(x)=a_1+a_3x+a_5x^2+\dots+a_{n-1}x^{\frac{n-2}{2}} \]

可以得出：

\[A(x)=A_1(x^2)+xA_2(x^2) \]

假设 \(k<\frac{n}{2}\)，将 \(\omega_n^k\) 作为 \(x\) 代入到 \(A(x)\) 中，有：

\[\begin{align} A(\omega_n^k) &= A_1(\omega_n^{2k})+\omega_n^kA_2(\omega_n^{2k})\\ &=A_1(\omega_{\frac{n}{2}}^k)+\omega_{n}^kA_2(\omega_{\frac{n}{2}}^k) \end{align} \]

再将 \(\omega_{n}^{k+\frac{n}{2}}\) 作为 \(x\) 代入到 \(A(x)\) 中，有：

\[\begin{align} A(\omega_{n}^{k+\frac{n}{2}}) &=A_1(\omega_{n}^{2k+n})+\omega_{n}^{k+\frac{n}{2}}A_2(\omega_{n}^{2k+n})\\ &=A_1(\omega_{n}^{2k}\omega_{n}^{n})-\omega_{n}^{k}A_2(\omega_{n}^{2k}\omega_n^n)\\ &=A_1(\omega_\frac{n}{2}^k)-\omega_n^kA_2(\omega_{\frac{n}{2}}^k) \end{align} \]

对比上述的两个式子可以发现，只是加减的不同，只要求出了 \(A_1(\omega_\frac{n}{2}^k)\) 和 \(\omega_n^kA_2(\omega_{\frac{n}{2}}^k)\) 的值，就可以同时获得 \(A(\omega_n^k)\) 和 \(A(\omega_{n}^{k+\frac{n}{2}})\) 的值。如果采用递归分治的方式来实现，每次回溯的时候只扫前面一半的序列，即可得出后面一半序列的答案。\(n=1\) 时，只有一个常数，直接\(\text{return}\) 即可，复杂度：\(O(n\log_2n)\)。

IFFT（快速傅里叶逆变换）

通过 \(\text{FFT}\) ，我们可以得出两个多项式相乘的积的点值表示法，接下来考虑如何将点值表示法转化为系数表示法。

IDFT

将单位复根代入多项式后，可得：

\[\left[ \begin{matrix} y_0\\ y_1\\ y_2\\ y_3\\ \vdots \\ y_{n-1} \end{matrix} \right]= \left[ \begin{matrix} 1 &1 &1 &1 &\cdots &1\\ 1 &\omega_n^1 &\omega_n^2 &\omega_n^3 &\cdots &\omega_n^{n-1}\\ 1 &\omega_n^2 &\omega_n^{4} &\omega_n^6 &\cdots &\omega_n^{2(n-1)}\\ 1 &\omega_n^3 &\omega_n^{6} &\omega_n^9 &\cdots &\omega_n^{3(n-1)}\\ \vdots &\vdots &\vdots &\vdots &\ddots &\vdots\\ 1 &\omega_n^{n-1} &\omega_n^{2(n-1)} &\omega_n^{3(n-1)} &\cdots &\omega_n^{(n-1)^2}\\ \end{matrix} \right] \left[ \begin{matrix} a_0\\ a_1\\ a_2\\ a_3\\ \vdots\\ a_{n-1} \end{matrix} \right] \]

其中，代入的 \(x_i=\omega_n^i\)。

现在，我们已知最左边的值和中间的大矩阵中 \(x\) 对应的各个值。根据矩阵的知识可以知道，只要在左右两边同时左乘上中间大矩阵的逆矩阵，即可求出系数矩阵。而中间的矩阵的元素十分的特殊，因此其逆矩阵也具有特殊的性质：即每一项取倒数，再乘上 \(n\) ，就可以得到其逆矩阵（这就是为什么要代入 \(\omega_n^i\) 的原因）。

为了取倒数，根据单位复根的性质和欧拉公式，有：

\[\frac{1}{\omega_n}=\omega_n^{-1}=e^{-\frac{2\pi i}{n}}=\cos\left(\frac{2\pi}{n}\right)-i·\sin\left(\frac{2\pi}{n}\right) \]

其中，\(i\) 是虚数单位，欧拉公式：\(e^{ix}=\cos(x)+i\sin(x)\)。

取倒数时，每一项乘上单位根的共轭复数即可。然后再分别乘上 \(n\) 就可以得到逆矩阵。

结论：一个多项式在分治过程中乘上单位复根的共轭复数，分治完的每一项除以 \(n\) 即为原多项式的每一项系数。也就说 \(\text{FFT}\) 和 \(\text{IFFT}\) 可以同时进行。

\(\text{C++}\) 有自带的复数模板：\(\text{complex库}\)。\(\text{a.real()}\) 即表示复数 \(a\) 的实部，\(\text{a.imag()}\) 表示虚部。

由于递归的写法常数比较大，因此此处只给出非递归的形式。

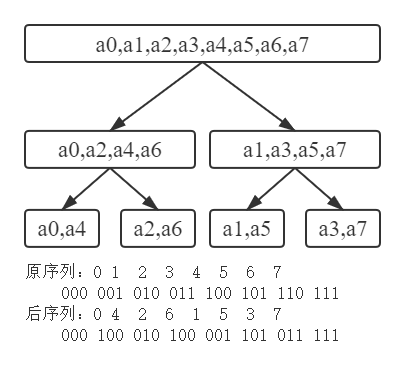
观察上图可以发现规律：原来的那个序列，每个数用二进制表示，然后把二进制翻转对称一下，就是最终那个位置的下标。该变换称为 蝴蝶变换。实际上，蝴蝶变换可以 \(O(n)\) 从小到大递推实现，设 \(len=2^k\)，其中 \(k\) 表示二进制数的长度，设 \(R(x)\) 表示长度为 \(k\) 的二进制数 \(x\) 翻转后的数（高位补 \(0\)）。那么，我们要求的是：\(R(0),R(1),\cdots,R(n-1)\)。

蝴蝶变换

首先，有 \(R(0)=0\)。

从小到大求 \(R(x)\)，那么当求 \(R(x)\) 时，\(R(\lfloor\frac{x}{2} \rfloor)\) 是已知的。因此，我们把 \(x\) 右移一位（除以 \(2\)），然后取反，再右移一位，就可以得到 \(x\) 除了二进制最低位外其它位的翻转结果。考虑最低位翻转的结果，若为 \(0\) 则，则翻转后最高位是 \(0\) ；否则为 \(1\)，那么还要加上 \(\frac{len}{2}=2^{k-1}\)。

综上所述：

\[R(x)=\left \lfloor \frac{R(\lfloor \frac{x}{2}\rfloor)}{2} \right\rfloor+(x \bmod 2)\times\frac{len}{2} \]

蝴蝶变换模板

// 需要保证 len 是 2 的幂
// 记 rev[i] 为 i 翻转后的值
void change(cp *pn, int len) 
{
	for(int i=0;i<len;i++)
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(cnt-1));
    for(int i=0;i<len;i++)
    {
        if(i<rev[i]) swap(pn[i],pn[rev[i]]);
    }
}

这样的话，就可以预先处理好每个位置的最终位置，再一步步的向上合并，复杂度：\(O(n)\)。

模板

loj108多项式乘法

输入 \(n\) 和 \(m\)，分别表示两个多项式的最高项次数。

\(0\leq n,m \leq 10^5\)

采用 \(\text{C++}\) 自带的 \(\text{complex}\) 复数类，但运行没有自己写快。

#include<bits/stdc++.h>
#define N 2621450
#define pi acos(-1) 
using namespace std;
typedef complex<double> E;
int n,m,l,r[N];
E a[N],b[N];
void fft(E *a,int f){
    for(int i=0;i<n;i++)if(i<r[i])swap(a[i],a[r[i]]);
    for(int i=1;i<n;i<<=1){
        E wn(cos(pi/i),f*sin(pi/i)); 
        for(int p=i<<1,j=0;j<n;j+=p){
            E w(1,0);
            for(int k=0;k<i;k++,w*=wn){
                E x=a[j+k],y=w*a[j+k+i];
                a[j+k]=x+y;a[j+k+i]=x-y;  
            }
        }
    }
}
inline int read(){
    int f=1,x=0;char ch;
    do{ch=getchar();if(ch=='-')f=-1;}while(ch<'0'||ch>'9');
    do{x=x*10+ch-'0';ch=getchar();}while(ch>='0'&&ch<='9');
    return f*x;
}
int main(){
    n=read();m=read();
    for(int i=0;i<=n;i++)a[i]=read();
    for(int i=0;i<=m;i++)b[i]=read();
    m+=n;for(n=1;n<=m;n<<=1)l++;
    for(int i=0;i<n;i++)r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
    fft(a,1);fft(b,1);
    for(int i=0;i<=n;i++)a[i]=a[i]*b[i];
    fft(a,-1);
    for(int i=0;i<=m;i++)printf("%d ",(int)(a[i].real()/n+0.5));
}

自己构造结构体表示复数，比直接用库快一点。

#include <bits/stdc++.h>

using namespace std;
const int N=1e5+5;
const double pi=acos(-1);
int a[N],b[N],rev[N<<2];
struct cp
{
    double x,y;
    cp(double tx=0.0,double ty=0.0)
    {
        x=tx;
        y=ty;
    }
    cp operator +(const cp &t)const
    {
        return cp(x+t.x,y+t.y);
    }
    cp operator -(const cp &t)const
    {
        return cp(x-t.x,y-t.y);
    }
    cp operator *(const cp &t)const
    {
        return cp(x*t.x-y*t.y,x*t.y+y*t.x);
    }
}A[N<<2],B[N<<2];
void read(int &x)
{
    x=0;
    int f=1;
    char ch;
    ch=getchar();
    while(!isdigit(ch))
    {
        if(ch=='-') f=-1;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        x=(x<<3)+(x<<1)+ch-'0';
        ch=getchar();
    }
    x*=f;
}
void swp(cp &u,cp &v)
{//交换记得要用引用
    cp t=u;
    u=v;
    v=t;
}
//f=1:FFT,f=-1:IFFT
void FFT(cp *pn,int len,int f)
{
    for(int i=0;i<len;i++)
        if(i<rev[i]) swp(pn[i],pn[rev[i]]);
    for(int i=1;i<len;i<<=1)//模拟合并过程，根据分治的公式理解
    {
        cp wn(cos(pi/i),f*sin(pi/i));//求单位复根，此时n=2*i
        for(int j=0,d=(i<<1);j<len;j+=d)
        {
            cp w(1,0);
            for(int k=0;k<i;k++)
            {
                cp u=pn[j+k],v=w*pn[j+k+i];
                pn[j+k]=u+v,pn[j+k+i]=u-v;
                w=w*wn;
            }
        }
    }
    if(f==-1)//IFFT
    {
        for(int i=0;i<len;i++)
            pn[i].x/=len;
    }
}
int main()
{
    int n,m;
    read(n),read(m);
    for(int i=0;i<=n;i++) read(a[i]);
    for(int i=0;i<=m;i++) read(b[i]);
    int len=1,cnt=0;
    while(len<n+m+1)//保证len是2的整数次幂
    {
        len<<=1;
        cnt++;
    }
    //先求出变换后位置:
    for(int i=0;i<len;i++)
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(cnt-1));
    for(int i=0;i<len;i++)
    {
        if(i<=n) A[i]=cp(a[i],0);
        else A[i]=cp(0,0);
        if(i<=m) B[i]=cp(b[i],0);
        else B[i]=cp(0,0);
    }
    //系数表示转点值表示：
    FFT(A,len,1);
    FFT(B,len,1);
    //求出最终结果的点值表示：
    for(int i=0;i<len;i++)
        A[i]=A[i]*B[i];
    //点值表示转系数表示：
    FFT(A,len,-1);
    for(int i=0;i<=n+m;i++)
        printf("%d%c",(int)(A[i].x+0.5),i==n+m?'\n':' ');
    return 0;
}

参考博客：

https://blog.csdn.net/enjoy_pascal/article/details/81478582?depth_1-

https://oi-wiki.org/math/poly/fft/

FFT 字符串匹配

FFT还能字符串匹配？

假设现在又两个字符串：\(S,T\),令 \(n=|S|,m=|T|\)，且有 \(n\geq m\)，串都从 \(0\) 开始存。

若 \(S\) 串的从第 \(i\) 个字符开始和 \(T\) 串匹配，即：

\[\sum_{j=0}^{m-1}{(S[i+j]-T[j])=0} \]

但是，上式还存在问题。因为受到正负的影响，可能导致 'ab'='ba' 的情况出现。

因此，对上式进行改变，有：

\[\sum_{j=0}^{m-1}{(S[i+j]-T[j])^2}\ (0\leq j<m) \]

当其为 \(0\) 时，就可以表示 \(S\) 的一个子串和 \(T\) 匹配。

但是上式仍然没有什么特殊之处，继续变换。将 \(T\) 串进行前后翻转，那么当 \(S\) 从位置 \(i\) 开始和 \(T\) 串匹配时，就有：\(S[i]=T[m-1],S[i+j]=T[m-1-j],\cdots\) ，因此当满足下列公式：

\[\sum_{j=0}^{m-1}{(S[i+j]-T[m-1-j])^2}=0 \]

可以说明达到匹配。

可以发现：\(i+j+m-1-j=m-i-1\) 是一个定值，即多项式乘法 \(F=S*T\) 的 \(F(m-i-1)\) 就可以表示 \(S[i,i+1,\cdots]\) 和串 \(T[0,1,2,\cdots,m-1]\) 的匹配情况。将平方拆开，得到 \(3\) 个多项式的和的形式：

\[\sum_{j=0}^{m-1}{(S[i+j]-T[m-1-j])^2}=\sum_{j=0}^{m-1}{S[i+j]^2}+\sum_{j=0}^{m-1}{T[m-1-j]^2}-2·\sum_{j=0}^{m-1}{(S[i+j]*T[m-1-j])} \]

前两项，可以直接预处理前缀和。对于后面的一项，可以令：

\[g(i)=2*\sum_{j=0}^{m-1}{(S[i+j]*T[m-1-j])} \]

枚举 \(i\) ，求出每个 \(g(i)\)，这个就可以用 \(\text{FFT}\) 来优化了，复杂度：\(O(n\log_2n)\)。

复杂度还没有KMP优秀

Rock Paper Scissors Lizard Spock.

https://nanti.jisuanke.com/t/A1676

枚举胜利的情况，把答案累加起来。此时，只需要计算 \(g(i)\) 即可（我把整个式子都算出来，死活调不对）。

代码

#include <bits/stdc++.h>

using namespace std;
typedef pair<char,char>pcc;
const double pi=acos(-1);
const int N=1e6+5;
typedef long long ll;
char s[N],t[N];
pcc f[13];
int rev[N<<2],res[N<<2];
struct cp
{
    double x,y;
    cp (double tx=0.0,double ty=0.0)
    {
        x=tx;
        y=ty;
    }
    cp operator +(const cp &t)const
    {
        return cp(x+t.x,y+t.y);
    }
    cp operator -(const cp &t)const
    {
        return cp(x-t.x,y-t.y);
    }
    cp operator *(const cp &t)const
    {
        return cp(x*t.x-y*t.y,x*t.y+y*t.x);
    }
}A[N<<2],B[N<<2];
void init()
{//胜利的情况
    f[1]=make_pair('S','P');
    f[2]=make_pair('S','L');
    f[3]=make_pair('P','R');
    f[4]=make_pair('P','K');
    f[5]=make_pair('R','L');
    f[6]=make_pair('R','S');
    f[7]=make_pair('L','P');
    f[8]=make_pair('L','K');
    f[9]=make_pair('K','R');
    f[10]=make_pair('K','S');
}
void swp(cp &u,cp &v)
{
    cp t=u;
    u=v;
    v=t;
}
void FFT(cp *pn,int len,int f)
{
    for(int i=0;i<len;i++)
        if(i<rev[i]) swp(pn[i],pn[rev[i]]);
    for(int i=1;i<len;i<<=1)
    {
        cp wn(cos(pi/i),f*sin(pi/i));
        for(int j=0,d=(i<<1);j<len;j+=d)
        {
            cp w(1,0);
            for(int k=0;k<i;k++)
            {
                cp u=pn[j+k],v=w*pn[j+k+i];
                pn[j+k]=u+v,pn[j+k+i]=u-v;
                w=w*wn;
            }
        }
    }
    if(f==-1)
    {
        for(int i=0;i<len;i++)
            pn[i].x/=len;
    }
}
int main()
{
    init();
    scanf("%s",s);
    scanf("%s",t);
    int n=strlen(s),m=strlen(t);
    int ans=0,len=1,maxn=n+m+1,cnt=0;
    while(len<maxn)
    {
        len<<=1;
        cnt++;
    }
    for(int i=0;i<len;i++)
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(cnt-1));
    reverse(t,t+m);
    for(int i=1;i<=10;i++)
    {
        for(int j=0;j<len;j++)
            A[j]=cp(0,0),B[j]=cp(0,0);
        for(int j=0;j<m;j++)
        {
            if(t[j]==f[i].first)
                A[j]=cp(1,0);
        }
        for(int j=0;j<n;j++)
        {
            if(s[j]==f[i].second)
                B[j]=cp(1,0);
        }
        FFT(A,len,1);
        FFT(B,len,1);
        for(int j=0;j<len;j++) A[j]=A[j]*B[j];
        FFT(A,len,-1);
        for(int j=0;j<=len;j++)
            res[j]+=(int)(A[j].x+0.5);
    }
    for(int i=m-1;i<n;i++)//根据公式，i从m-1开始
        ans=max(ans,res[i]);
    printf("%d\n",ans);
    return 0;
}