*Minimum-cost Flow【网络流】

题意：

给出一个 \(n\) 点，\(m\) 条边有向图，点 \(a_i\) 到 \(b_i\) 的花费为 \(c_i\)，并且每条边的容量限制相同。\(q\) 次询问，每次给出两个数 \(u_i\) 和 \(v_i\) ，每条边的容量限制为 \(\frac{u_i}{v_i}\)，每从 \(1\) 号点运送 \(1\) 个单位的物品，如果能够全部送达 \(n\)，求出最小花费。否则，输出 \('NaN'\)。

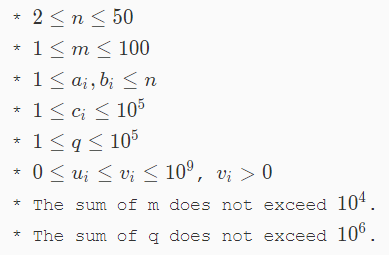
分析：

将 \(x\) 个单位的物品通过 \(y\) 的限制的通道从 \(1\) 运到 \(n\) 的花费记作：\(cost(x,y)\)。那么要求 \(cost(1,\frac{u_i}{v_i})=cost(\frac{v_i}{u_i},1)*\frac{u_i}{v_i}\)。当每条边的容量固定为 \(1\) 时，可以直接用最小费用最大流求出每一条增广路径的花费，而且花费越小的增广路越先被走。当求出总的路径条数 \(tol\) ，即此时的最大流量。用 \(tol*\frac{u_i}{v_i} \geq 1\)，判断是否可以满足要求。当满足要求时，为了最小费用，肯定按路径从小到大走。对于此时要求的流量 \(\frac{v_i}{u_i}\)，将其分配到路径中，求出花费，然后乘 \(\frac{u_i}{v_i}\) 即可。
https://ac.nowcoder.com/acm/contest/5666/H

代码：

#include<bits/stdc++.h>
#define pb push_back
using namespace std;
typedef long long ll;
typedef pair<int,int>pii;
const int N=55;
const int inf=0x3f3f3f3f;
int ec[N<<1];//存每条增广路的花费
int flow[N],n,dis[N];
bool vis[N];
struct Node
{
    int to,val,cost,rev;
};
vector<Node>pic[N];
queue<int>que;
pii pre[N];//存上一个点
void add(int u,int v,int w,int c)
{
    pic[u].pb({v,w,c,pic[v].size()});
    pic[v].pb({u,0,-c,pic[u].size()-1});
}
bool spfa()
{
    while(!que.empty())
        que.pop();
    for(int i=1;i<=n;i++)
    {
        dis[i]=inf;
        flow[i]=inf;//存增广路的最小流量
        vis[i]=false;
    }
    dis[1]=0;
    vis[1]=true;
    que.push(1);
    while(!que.empty())
    {
        int now=que.front();
        que.pop();
        vis[now]=false;
        for(int i=0;i<pic[now].size();i++)
        {
            Node tmp=pic[now][i];
            if(dis[tmp.to]>dis[now]+tmp.cost&&tmp.val>0)
            {
                dis[tmp.to]=dis[now]+tmp.cost;
                vis[tmp.to]=true;
                flow[tmp.to]=min(flow[now],tmp.val);
                pre[tmp.to]=make_pair(now,i);
                que.push(tmp.to);
            }
        }
    }
    return dis[n]<inf;
}
void EK(int &tol)
{
    tol=0;
    while(spfa())
    {
        int mf=flow[n];
        for(int i=n;i!=1;i=pre[i].first)
        {
            pii d=pre[i];
            pic[d.first][d.second].val-=mf;
            pic[i][pic[d.first][d.second].rev].val+=mf;
        }
        tol++;
        ec[tol]=ec[tol-1]+mf*dis[n];//前缀和
    }
}
ll gcd(ll a,ll b)
{
    return b?gcd(b,a%b):a;
}
int main()
{
    int m,a,b,c,q,u,v;
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        int tol=0;
        for(int i=1;i<=n;i++)
            pic[i].clear();
        for(int i=1;i<=m;i++)
        {
            scanf("%d%d%d",&a,&b,&c);
            add(a,b,1,c);//转化为边的容量为1
        }
        EK(tol);
        scanf("%d",&q);
        while(q--)
        {
            ll ans=-1,g=1;
            scanf("%d%d",&u,&v);
            if(1LL*tol*u>=v)
            {
                int d=v/u,r=v%u;
                if(d+(r>0)<=tol)
                {
                    ans=1LL*ec[d]*u;
                    if(r>0)
                        ans=ans+1LL*(ec[d+1]-ec[d])*r;
                    g=gcd(ans,1LL*v);
                }
            }
            if(ans==-1) printf("NaN\n");
            else printf("%lld/%lld\n",ans/g,v/g);
        }
    }
    return 0;
}