矩阵快速幂（HDU-1757&&HDU-2604）

A Simple Math Problem HDU-1757

Lele now is thinking about a simple function f(x).

If x < 10 f(x) = x.
If x >= 10 f(x) = a0 * f(x-1) + a1 * f(x-2) + a2 * f(x-3) + …… + a9 * f(x-10);
And ai(0<=i<=9) can only be 0 or 1 .

Now, I will give a0 ~ a9 and two positive integers k and m ,and could you help Lele to caculate f(k)%m.

InputThe problem contains mutiple test cases.Please process to the end of file.
In each case, there will be two lines.
In the first line , there are two positive integers k and m. ( k<2*10^9 , m < 10^5 )
In the second line , there are ten integers represent a0 ~ a9.
Output

For each case, output f(k) % m in one line.

Sample Input

10 9999
1 1 1 1 1 1 1 1 1 1
20 500
1 0 1 0 1 0 1 0 1 0

Sample Output

45
104

矩阵快速幂的关键是由F(n-1)、F(n-2)、F(n-3).....怎么得到F(n)、F(n-1)、F(n-2).....此题将F(n-1)、F(n-2)、F(n-3).....看成矩阵A，它们的系数看成矩阵B，因为F(n)=a0 * F(n-1) + a1 * F(n-2) + a2 * F(n-3) + …… + a9 * F(n-10)，所以B矩阵第一行填a0、a1、a2.....a9。第二行由F(n-1)、F(n-2)、F(n-3).....得到F(n-1)，所以第二行填1 0 0 0.....以此类推，矩阵如下图所示：

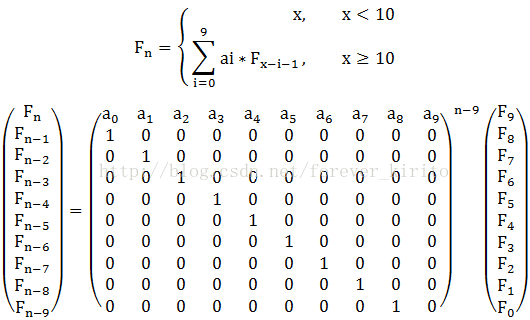
 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 using namespace std;
 5 typedef long long ll;
 6 ll k,mod;
 7 struct node{
 8     int m[15][15];
 9 }a,b;
10 void init()
11 {
12     memset(a.m,0,sizeof(a.m));
13     memset(b.m,0,sizeof(b.m));
14     for(int i=1;i<10;i++)
15     {
16         a.m[i][i-1]=1;
17     }
18     for(int i=0;i<10;i++)
19     {
20         b.m[i][i]=1;
21     }
22 }
23 node mul(node aa,node bb)
24 {
25     node c;
26     for(int i=0;i<10;i++)
27     {
28         for(int j=0;j<10;j++)
29         {
30             c.m[i][j]=0;
31             for(int k=0;k<10;k++)
32             {
33                 c.m[i][j]+=(aa.m[i][k]*bb.m[k][j])%mod;
34             }
35             c.m[i][j]%=mod;
36         }
37     } 
38     return c;
39 }
40 node pow_mod(node aa,node bb,int t)
41 {
42     while(t)
43     {
44         if(t&1)
45         {
46             bb=mul(aa,bb); 
47         }
48         aa=mul(aa,aa);
49         t>>=1; 
50     }
51 return bb;
52 }
53 int main()
54 {
55     while(~scanf("%lld%lld",&k,&mod))
56     {
57         init();
58         for(int i=0;i<10;i++)
59         {
60             scanf("%d",&a.m[0][i]);
61         }
62         if(k<=9)
63         {
64             printf("%d\n",k%mod);
65             continue;
66         }
67         else
68         {
69             node res=pow_mod(a,b,k-9);
70             ll ans=0;
71             for(int i=0;i<10;i++)
72             {
73                 ans+=res.m[0][i]*(9-i)%mod;
74             }
75             printf("%lld\n",ans%mod);
76         }
77     }
78 }
79

心得：一般矩阵快速幂的题求某个矩阵的多少次幂是看该矩阵从第几项开始满足矩阵快速幂乘法的。比如这个题前九项并不满足矩阵乘法，所以pow_mod里面的幂项是k-9（一般是前多少项不满足就减几）。

而pow_mod函数返回的值为矩阵乘完后的值，保存在res.m[0][i]中，最后ans为res.m[0][i]与前多少项不满足矩阵乘法的项的值的乘积。

Queuing HDU-2604

Queues and Priority Queues are data structures which are known to most computer scientists. The Queue occurs often in our daily life. There are many people lined up at the lunch time.

Now we define that ‘f’ is short for female and ‘m’ is short for male. If the queue’s length is L, then there are 2 ^L numbers of queues. For example, if L = 2, then they are ff, mm, fm, mf . If there exists a subqueue as fmf or fff, we call it O-queue else it is a E-queue.
Your task is to calculate the number of E-queues mod M with length L by writing a program.

InputInput a length L (0 <= L <= 10 ⁶) and M.OutputOutput K mod M(1 <= M <= 30) where K is the number of E-queues with length L.Sample Input

3 8
4 7
4 8

Sample Output

6
2
1

本题的关键是推出f(n)=f(n-1)+f(n-3)+f(n-4)

  1 #include<iostream>
  2 #include<cstdio>
  3 #include<cstring>
  4 using namespace std;
  5 typedef long long ll;
  6 ll l,mod;
  7 struct node{
  8     int m[15][15];
  9 }a,b;
 10 void init()
 11 {
 12     memset(a.m,0,sizeof(a.m));
 13     for(int i=0;i<4;i++)
 14     {
 15         if(i!=1)
 16             a.m[0][i]=1;
 17     }
 18     for(int i=1;i<4;i++)
 19     {
 20         a.m[i][i-1]=1;
 21     }
 22     memset(b.m,0,sizeof(b.m));
 23     for(int i=0;i<4;i++)
 24     {
 25         b.m[i][i]=1;
 26     }
 27 }
 28 node mul(node aa,node bb)
 29 {
 30     node c;
 31     for(int i=0;i<4;i++)
 32     {
 33         for(int j=0;j<4;j++)
 34         {
 35             c.m[i][j]=0;
 36             for(int k=0;k<4;k++)
 37             {
 38                 c.m[i][j]+=(aa.m[i][k]*bb.m[k][j])%mod;
 39             }
 40             c.m[i][j]%=mod;
 41         }
 42     }
 43 return c;
 44 }
 45 node pow_mod(node aa,node bb,int x)
 46 {
 47     while(x)
 48     {
 49         if(x&1)
 50         {
 51             bb=mul(aa,bb);
 52         }
 53         aa=mul(aa,aa);
 54         x>>=1;
 55     }
 56 return bb;
 57 }
 58 int f[4]={2,4,6,9};
 59 int main()
 60 {
 61     while(~scanf("%lld%lld",&l,&mod))
 62     {
 63         init();
 64         if(l<=4)
 65         {
 66             if(l==0)
 67             {
 68                 printf("0\n");
 69                 continue; 
 70             }
 71             if(l==1)
 72             {
 73                 printf("%lld\n",2%mod);
 74                 continue;
 75             }
 76             if(l==2)
 77             {
 78                 printf("%lld\n",4%mod);
 79                 continue;
 80             }
 81             if(l==3)
 82             {
 83                 printf("%lld\n",6%mod);
 84                 continue;
 85             } 
 86             if(l==4)
 87             {
 88                 printf("%lld\n",9%mod);
 89                 continue;
 90             } 
 91         }
 92     node res=pow_mod(a,b,l-4);
 93         int ans=0;  
 94       for(int i=0;i<4;i++)
 95       {
 96           ans+=f[3-i]*res.m[0][i]%mod;
 97       }
 98       printf("%lld\n",ans%mod);
 99     }
100 }

posted @ 2018-08-20 21:41 *starry* 阅读(182) 评论(0) 编辑收藏举报

*starry*

矩阵快速幂（HDU-1757&&HDU-2604）

A Simple Math Problem HDU-1757

Queuing HDU-2604

公告

starry