树状数组（入门+一维+二维）

树状数组

 

 
C[i]代表 子树的叶子结点的权值之和

 

如图可以知道

 

C[1]=A[1];

 

C[2]=A[1]+A[2];

 

C[3]=A[3];

 

C[4]=A[1]+A[2]+A[3]+A[4];

 

C[5]=A[5];

 

C[6]=A[5]+A[6];

 

C[7]=A[7];

 

C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];
将C[]数组的结点序号转化为二进制
1=(001)      C[1]=A[1];
2=(010)      C[2]=A[1]+A[2];
3=(011)      C[3]=A[3];
4=(100)      C[4]=A[1]+A[2]+A[3]+A[4];
5=(101)      C[5]=A[5];
6=(110)      C[6]=A[5]+A[6];
7=(111)      C[7]=A[7];
8=(1000)    C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];
对照式子可以发现  C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i]; （k为i的二进制中从最低位到高位连续零的长度）例如i=8时，k=3;
现在引入lowbit(x) 
lowbit(x) 其实就是取出x的最低位1  换言之  lowbit(x)=2^k  k的含义与上面相同 
C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i];
C[i]=A[i-lowbit(i)+1]+A[i-lowbit(i)+2]+......A[i];
 
区间查询
下面利用C[i]数组，求A数组中前i项的和 
举个例子 i=7;
sum[7]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7] ;   前i项和
C[4]=A[1]+A[2]+A[3]+A[4];   C[6]=A[5]+A[6];   C[7]=A[7];
可以推出:   sum[7]=C[4]+C[6]+C[7];
序号写为二进制: sum[(111)]=C[(100)]+C[(110)]+C[(111)];
 
再举个例子 i=5
sum[7]=A[1]+A[2]+A[3]+A[4]+A[5] ;   前i项和
C[4]=A[1]+A[2]+A[3]+A[4];   C[5]=A[5];
可以推出:   sum[5]=C[4]+C[5];
序号写为二进制: sum[(101)]=C[(100)]+C[(101)];
 
细细观察二进制 树状数组追其根本就是二进制的应用
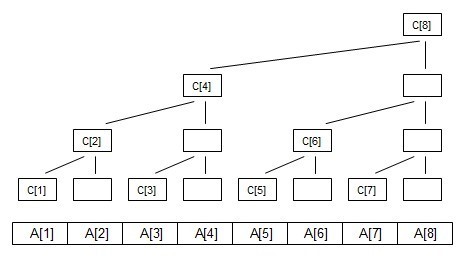
int getsum(int x)
{
    int ans=0;
    for(int i=x;i>0;i-=lowbit(i))
    ans+=C[i];
    return ans；
}
单点更新
 
当我们修改A[]数组中的某一个值时  应当如何更新C[]数组呢？
回想一下 区间查询的过程，再看一下上文中列出的图
void add(int x,int y)
{
    for(int i=x;i<=n;i+=lowbit(i))
    tree[i]+=y;
}
//可以发现 更新过程是查询过程的逆过程
//由叶子结点向上更新C[]数组

当更新A[1]时  需要向上更新C[1] ,C[2],C[4],C[8]
                     C[1],   C[2],    C[4],     C[8]
写为二进制  C[(001)],C[(010)],C[(100)],C[(1000)]
                          1(001)     C[1]+=A[1]
lowbit(1)=001 1+lowbit(1)=2(010)     C[2]+=A[1]
lowbit(2)=010 2+lowbit(2)=4(100)     C[4]+=A[1]
lowbit(4)=100 4+lowbit(4)=8(1000)    C[8]+=A[1]
例题：Ultra-QuickSort  
 In this problem, you have to analyze a particular sorting algorithm. The algorithm processes a sequence of n distinct integers by swapping two adjacent sequence elements until the sequence is sorted in ascending order. For the input sequence 
9 1 0 5 4 ,

Ultra-QuickSort produces the output 
0 1 4 5 9 .

Your task is to determine how many swap operations Ultra-QuickSort needs to perform in order to sort a given input sequence.InputThe input contains several test cases. Every test case begins with a line that contains a single integer n < 500,000 -- the length of the input sequence. Each of the the following n lines contains a single integer 0 ≤ a[i] ≤ 999,999,999, the i-th input sequence element. Input is terminated by a sequence of length n = 0. This sequence must not be processed.OutputFor every input sequence, your program prints a single line containing an integer number op, the minimum number of swap operations necessary to sort the given input sequence.Sample Input 
5
9
1
0
5
4
3
1
2
3
0
Sample Output 
6
0
 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 using namespace std;
 6 const int maxn=1000010;
 7 int t[maxn];
 8 int lowbit(int x)
 9 {
10     return x&(-x);
11 }
12 void update(int pos)
13 {
14     while(pos<maxn)
15     {
16         ++t[pos];
17         pos+=lowbit(pos);
18     }
19 }
20 long long query(int pos)
21 {
22     long long cnt=0;
23     while(pos>0)
24     {
25         cnt+=t[pos];
26         pos-=lowbit(pos);
27     }
28     return cnt;
29 }
30 int main()
31 {
32     int n;
33     while(~scanf("%d",&n))
34     {
35         if(n==0)
36             break;
37         memset(t,0,sizeof(t));
38         long long sum=0;
39         for(int i=0;i<n;i++)
40         {
41             int temp;
42             scanf("%d",&temp);
43             int count=query(temp+1);//temp+1防止出现0造成死循环 
44             sum+=i-count;//count求出的是该数前面出现的比它小的数的个数，而本题让求逆序数，故用i-count 
45             update(temp+1);
46         }
47         printf("%lld\n",sum);
48     }
49 return 0;
50 }

二维树状数组 单点更新 区间查询

设原始二维数组为： 
A[][]={{a11,a12,a13,a14,a15,a16,a17,a18,a19}, 
{a21,a22,a23,a24,a25,a26,a27,a28,a29}, 
{a31,a32,a33,a34,a35,a36,a37,a38,a39}, 
{a41,a42,a43,a44,a45,a46,a47,a48,a49}};

记: 
B[1]={a11,a11+a12,a13,a11+a12+a13+a14,a15,a15+a16,…} 这是第一行的一维树状数组 
B[2]={a21,a21+a22,a23,a21+a22+a23+a24,a25,a25+a26,…} 这是第二行的一维树状数组 
B[3]={a31,a31+a32,a33,a31+a32+a33+a34,a35,a35+a36,…} 这是第三行的一维树状数组 
B[4]={a41,a41+a42,a43,a41+a42+a43+a44,a45,a45+a46,…} 这是第四行的一维树状数组

那么： 
C[1][1]=a11,C[1][2]=a11+a12,C[1][3]=a13,C[1][4]=a11+a12+a13+a14,c[1][5]=a15,C[1][6]=a15+a16,… 这是A[][]第一行的一维树状数组 
C[2][1]=a11+a21,C[2][2]=a11+a12+a21+a22,C[2][3]=a13+a23,C[2][4]=a11+a12+a13+a14+a21+a22+a23+a24,C[2][5]=a15+a25,C[2][6]=a15+a16+a25+a26,… 这是A[][]数组第一行与第二行相加后的树状数组 
C[3][1]=a31,C[3][2]=a31+a32,C[3][3]=a33,C[3][4]=a31+a32+a33+a34,C[3][5]=a35,C[3][6]=a35+a36,…这是A[][]第三行的一维树状数组 
C[4][1]=a11+a21+a31+a41,C[4][2]=a11+a12+a21+a22+a31+a32+a41+a42,C[4][3]=a13+a23+a33+a43,… 这是A[][]数组第一行+第二行+第三行+第四行后的树状数组

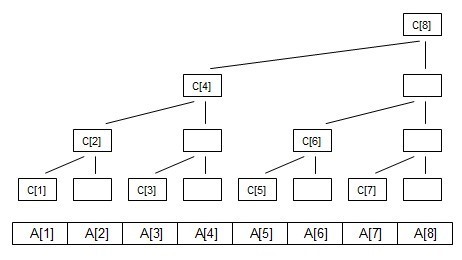
二维数组的规律就是,不管是横坐标还是纵坐标,将他们单独拿出来,他们都符合x += lowbit(x)，属于它的父亲节点，即都符合那个经典的图。比如C[4][2]： 
单独看横坐标（就是把纵坐标去掉，重复的只算一个）：C[4] = C[2]+C[3]+a[4] （经典图得出）= a[1]+a[2]+a[3]+a[4] （从上面公式得出） 
单独看纵坐标（就是把横坐标去掉，重复的只算一个）：C[2] = C[1]+a[2] （经典图得出）= a[1]+a[2] （上面公式得出）

还不明白就多看几遍，体会一下，应该就懂了。

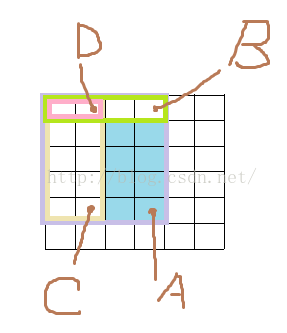
区间查询的话，调用一次query(x,y)显然是求(1,1) 到 (x,y)范围内矩形的和。观察下图，我们没办法一次查询出来给定区间的值，但是我们可以通过计算得出。 
现在如果要查询蓝色范围内的和 
调用A点是求紫色边框 
调用B点是求绿色边框 
调用C点是求黄色边框 
调用D点是求红色边框 
那么A-B-C+D即是答案。 

 

接下来以hdu2642为模板题来写一下二维树状数组的单点更新，区间查询。 
题意：一个星空，二维的。上面有1000*1000的格点,每个格点上有星星在闪烁。一开始时星星全部暗淡着，有M个操作： 
B x y 点亮一盏星星 
D x y 熄灭一盏星星 
Q x1 x2 y1 y2 查询这个矩形里面亮着的星星的个数。

题解：这就是个二维树状数组单点更新、区间查询的模板题，直接写即可。不过有几个需要注意的地方。就像我在一维里说的，树状数组下标是从1开始维护的，所以我们要把数据偏移到下标从1开始，二维里也是一样。这里坐标可能为0，所以我们把每个坐标都++，然后就是点亮的星星不能重复点亮，暗淡的星星不能重复暗淡，设一个状态的数组即可。

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 using namespace std;
 6 const int maxn=1100;
 7 int sz[maxn][maxn],status[maxn][maxn];
 8 int lowbit(int x)
 9 {
10     return x&(-x);
11 }
12 void update(int x,int y,int val)
13 {
14     for(int i=x;i<maxn;i+=lowbit(i))
15     {
16         for(int j=y;j<maxn;j+=lowbit(j))
17         {
18             sz[i][j]+=val;
19         }
20     }
21 }
22 int query(int x,int y)
23 {
24     int ans=0;
25     for(int i=x;i>0;i-=lowbit(i))
26     {
27         for(int j=y;j>0;j-=lowbit(j))
28         {
29             ans+=sz[i][j];
30         }
31     }
32     return ans;
33 } 
34 int main()
35 {
36     int T;
37     cin>>T;
38     memset(sz,0,sizeof(sz));
39     memset(status,0,sizeof(status));
40     char ch;
41     int x1,x2,y1,y2;
42     while(T--)
43     {
44         getchar();
45         scanf("%c",&ch);
46         if(ch=='B')
47         {
48             scanf("%d%d",&x1,&y1);
49             x1++;
50             y1++;
51             if(status[x1][y1]==0)
52             {
53                 update(x1,y1,1);
54                 status[x1][y1]=1;
55             }
56         }
57         if(ch=='D')
58         {
59             scanf("%d%d",&x1,&y1);
60             x1++;
61             y1++;
62             if(status[x1][y1]>0)
63             {
64                 update(x1,y1,-1);
65                 status[x1][y1]=0;
66             }
67         }
68         if(ch=='Q')
69         {
70             scanf("%d%d%d%d",&x1,&x2,&y1,&y2);
71             x1++; y1++;
72             x2++; y2++;
73             if(x2<x1)
74             {
75                 int t=x2;
76                 x2=x1;
77                 x1=t;
78             }
79             if(y2<y1)
80             {
81                 int t=y2;
82                 y2=y1;
83                 y1=t;
84             }
85           printf("%d\n",query(x2,y2)-query(x2,y1-1)-query(x1-1,y2)+query(x1-1,y1-1)); 
86         }
87     } 
88 }

参考博客：

http://www.cnblogs.com/hsd-/p/6139376.html

https://blog.csdn.net/WilliamSun0122/article/details/71642358

posted @ 2018-08-09 13:56  *starry*  阅读(272)  评论(0)  编辑  收藏  举报