1123 Is It a Complete AVL Tree (30分)---如何建立平衡二叉搜索树(LL型RR型LR型RL型)+如何判断完全二叉树
1123 Is It a Complete AVL Tree (30分)
An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.
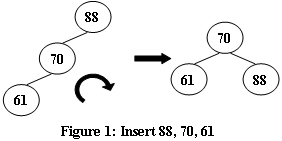 | 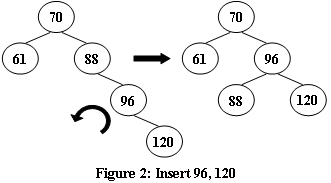 |
|---|---|
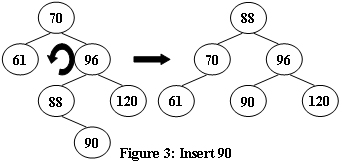 |
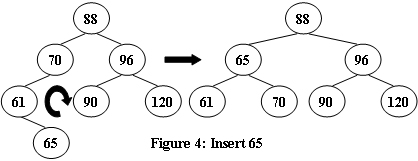 |
Now given a sequence of insertions, you are supposed to output the level-order traversal sequence of the resulting AVL tree, and to tell if it is a complete binary tree.
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (≤ 20). Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.
Output Specification:
For each test case, insert the keys one by one into an initially empty AVL tree. Then first print in a line the level-order traversal sequence of the resulting AVL tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line. Then in the next line, print YES if the tree is complete, or NO if not.
Sample Input 1:
5
88 70 61 63 65
Sample Output 1:
70 63 88 61 65
YES
Sample Input 2:
8
88 70 61 96 120 90 65 68
Sample Output 2:
88 65 96 61 70 90 120 68
NO
题解:参考陈越姥姥《数据结构》课本P132-141 层序遍历用bfs,queue中什么都可以存,可以存queue<struct node*>q;
1 #include<iostream>
2 #include<cstdio>
3 #include<stdlib.h>
4 #include<cstring>
5 #include<vector>
6 #include<queue>
7 #include<algorithm>
8 using namespace std;
9 typedef struct node * AVLTree;
10 struct node{
11 int high;
12 int data;
13 AVLTree left;
14 AVLTree right;
15 };
16 int n;
17 vector<int>v[110],ans;
18 int gethigh(AVLTree T)
19 {
20 if(T==NULL)
21 return 0;
22 int l=gethigh(T->left);
23 int r=gethigh(T->right);
24 return max(l,r)+1;
25 }
26 AVLTree SingleLeft(AVLTree T)
27 {
28 AVLTree B=T->left;
29 T->left=B->right;
30 B->right=T;
31 T->high=max(gethigh(T->left),gethigh(T->right))+1;
32 B->high=max(gethigh(B->left),T->high)+1;
33 return B;
34 }
35 AVLTree SingleRight(AVLTree T)
36 {
37 AVLTree B=T->right;
38 T->right=B->left;
39 B->left=T;
40 T->high=max(gethigh(T->left),gethigh(T->right))+1;
41 B->high=max(gethigh(B->right),T->high)+1;
42 return B;
43 }
44 AVLTree DoubleLeftRight(AVLTree T)
45 {
46 T->left=SingleRight(T->left);
47 return SingleLeft(T);
48 }
49 AVLTree DoubleRightLeft(AVLTree T)
50 {
51 T->right=SingleLeft(T->right);
52 return SingleRight(T);
53 }
54 AVLTree insert(AVLTree T,int x)
55 {
56 if(T==NULL)
57 {
58 T=(AVLTree)malloc(sizeof(struct node));
59 T->data=x;
60 T->high=1;
61 T->left=T->right=NULL;
62 }
63 else if(x<T->data)
64 {
65 T->left=insert(T->left,x);
66 if(gethigh(T->left)-gethigh(T->right)==2)
67 {
68
69 if(x<T->left->data)
70 T=SingleLeft(T);
71 else
72 T=DoubleLeftRight(T);
73 }
74 }
75 else if(x>T->data)
76 {
77 T->right=insert(T->right,x);
78 if(gethigh(T->left)-gethigh(T->right)==-2)
79 {
80 if(x>T->right->data)
81 T=SingleRight(T);
82 else
83 T=DoubleRightLeft(T);
84 }
85 }
86 return T;
87 }
88 void bfs(AVLTree T){
89 queue<AVLTree> q;
90 q.push(T);
91 //first:有没有出现没有左孩子或右孩子的节点
92 bool first=0,flag=1;
93 while(!q.empty()){
94 AVLTree now = q.front();
95 q.pop();
96 ans.push_back(now->data);
97 if(now->left!=NULL){
98 if(first) flag=0;
99 q.push(now->left);
100 }else first=1;
101 if(now->right!=NULL){
102 if(first) flag=0;
103 q.push(now->right);
104 }else first=1;
105 }
106 int siz=ans.size();
107 for(int i=0;i<siz;i++){
108 cout<<ans[i];
109 if(i!=siz-1)
110 cout<<" ";
111 }
112 cout<<endl;
113 puts(flag?"YES":"NO");
114
115 }
116 int main()
117 {
118 cin>>n;
119 int x;
120 AVLTree T=NULL;
121 for(int i=0;i<n;i++)
122 {
123 scanf("%d",&x);
124 T=insert(T,x);
125 }
126 bfs(T);
127 }




