由KTT展开的一系列知识点
首先为了便于理解,补充梯度方向这一概念
借鉴网址:https://baijiahao.baidu.com/s?id=1612682474674468619&wfr=spider&for=pc
首先我们来了解一下梯度的方向为什么会与等高线的切线方向垂直
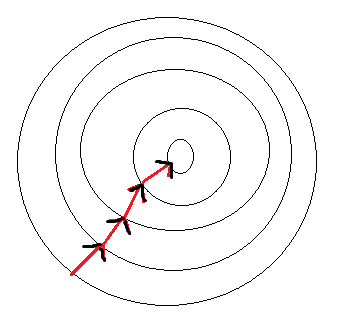
图1. 梯度介绍图
假设我们有几何上的一个曲面S,曲面被平面c截出的曲线L的方程为:z = f(x,y), z = c
该曲线L在xy轴面上的投影为一条平面曲线Q,它在xy平面直角坐标系中的方程为f(x, y) = c,该曲线Q为函数z = f(x, y)的等高线。
我们对f(x, y) = c的两边分别对x求导,故
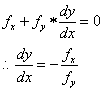
等高线f(x, y) = c上任一点的切线斜率为dy/dx,等高线上任意一点(x, y)处的法线的斜率为(切线与法线斜率乘积为-1)
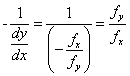
又因为梯度为:
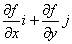
故梯度的方向为:
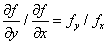
即梯度的方向和法线斜率相同,即梯度的方向与等高线切线方向垂直。
之后我们正式进入KKT
借鉴网址为:https://www.cnblogs.com/xinchen1111/p/8804858.html
对于简单的可求导的函数,我们直接求导,令导数为零,并加以判断(防止x^3导数为0的零并非是极值点的情况),即可求出极值点。
但是对于一些复杂问题,我们无法直接求导得出,为此即引入了梯度下降法、牛顿法和坐标下降法之类的数值迭代算法。
对于该类问题,我们可以抽象为在一个山群中,选取一个起始点,然后从该点开始,不断地向最低点靠近,直至到达最低为止。为此引申出了如下方法
1)梯度下降法
即依靠梯度确定下降方法,步骤如下
1.随机选取X0
2.得到函数在X0的梯度,然后从X0向前走一步,计算式为
![]()
3.重复步骤2,直到梯度接近0(小于之前设定的很小的数),或者达到指定的跌代上限
该图即如图1所示
2)坐标下降法
上述问题还可以这样解决,即在第2步中,首先固定x,将其作为常数,求导得到最优点,之后固定y,将y看做一个常数,再次求导。这样每次只优化一个变量的方法即坐标下降法。

3)有等式约束的问题
进一步就是有等式约束的问题
即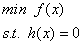
此时该问题不能仅仅由上述的梯度和求导得出,因为此时我们要求求满足约束的等值线和约束函数线的交点。
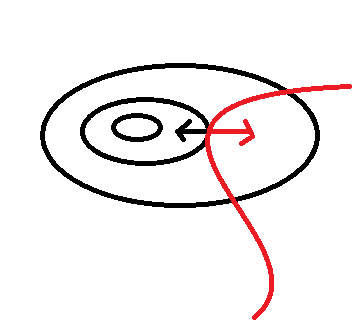
带约束的极值(红线为h(x),黑线为f(x,y))
此时我们可以看出极值点只能在等值线和函数相切的地方取到,因为如果不是相切的地方,则沿着h(x)的图像向前或者后走,都能找到f(x, y)更大或者更小的点,故交点不是极值点,当其相切时,才能报纸极值点。此外,相切的地方h(x)的梯度和f(x, y)的梯度应该是在一条直线上的。(因为在切点上,梯度都与切线垂直)
此时即![]()
求解该方程即可得出最优解。
当有多个等式约束的时候,目标函数的梯度和约束梯度的线性组合在一条直线上就能满足要求: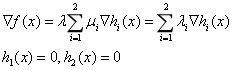
将原来的约束问题写为:![]()
之后对x和拉姆塔求偏导,让其为0,即可得到解,该函数叫做拉格朗日函数。
(4)对于不等式约束
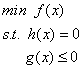
此时约束条件为:
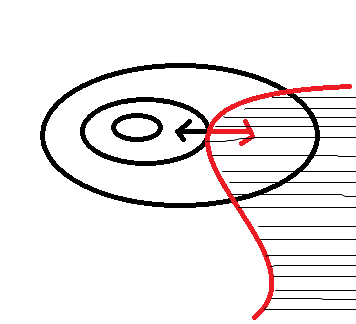
即可行域变成了阴影区域,能取到极值的地方有两种:
1)还是在线与等值线相切的地方
2)f(x)的极值点在可行域中
因为如果不是相切,那么同样的,对任意一个在可行域中的点,如果在它附近往里走或者往外走,f(x) 一般都会变大或者变小,所以绝大部分点都不会是极值点。除非这个点刚好在交界处,且和等值线相切;或者这个点在可行域内部,但是本身就是 f(x) 的极值点。

对于第一种情况,不等式约束仍旧是等式约束,对![]() ,用拉格朗日乘子法
,用拉格朗日乘子法
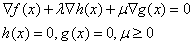
对于第二种情况,不等式约束就相当于没有,对![]() 用拉格朗日乘子法
用拉格朗日乘子法
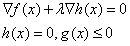
将两种情况合二为一,第一种情况中![]() ,第二种
,第二种![]() ,故综合可以写为
,故综合可以写为![]()
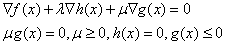
该条件即为KKT条件,即这个优化问题一定满足该方程组。(不是极值点也可能满足,但是不存在某极值点不满足),即原来的优化问题取得极值点的必要条件,解出来了极值代入验证。
KTT条件并不是任何情况都满足的,需要满足一些规范性条件,即要求约束条件的质量不能太差。
- LCQ:如果 h(x) 和 g(x) 都是形如 Ax+b的仿射函数,那么极值一定满足 KKT 条件。
- LICQ:起作用的 g(x) 函数(即 g(x)相当于等式约束的情况)和 h(x)函数在极值点处的梯度要线性无关,那么极值一定满足 KKT 条件。
- Slater 条件:如果优化问题是个凸优化问题,且至少存在一个点满足 h(x)=0和 g(x)=0,极值一定满足 KKT 条件。
KKT 条件虽然从理论上给出了极值的必要条件,但是一般实际解的时候直接方程也是很困难的(特别是约束很多的时候),一般也会采用罚函数法等数值方法。
为了更好的解决这个优化问题,数学家还找到了它的对偶问题。找一个优化问题的对偶问题的一般因为是对偶问题比原问题更好解决,并且对偶问题的解和原问题是一样的。上面的拉格朗日函数也可以看做原问题的对偶问题。



