ZROI 暑期高端峰会 A班 Day1 组合计数
AGC036F Square Constriants
一定有 \(l_i<p_i\le r_i\)。
考虑朴素容斥,枚举每个数是 \(\le l_i\) 还是 \(\le r_i\)。对于 \(p_i\le x_i\),方案数是:把 \(x\) 排序后 \(\prod(x_i+1-i)\)(下标从 \(0\) 开始)。
太慢了。
把 \(l_0\) 到 \(l_{n-1}\),\(r_0\) 到 \(r_{2n-1}\) 一起排序。(\(l_n\) 到 \(l_{2n-1}\) 不用管,他们非正)
把 \(l_0\) 到 \(l_{n-1}\) 叫 A 类数。
把 \(r_n\) 到 \(r_{2n-1}\) 叫 B 类数。
把 \(r_0\) 到 \(r_{n-1}\) 叫 C 类数。
那么排序后一定形如 ABBAABABABACCCCCCC...。
所有 B 都要选, 每对 AC 中选一个。
先枚举一共选了多少个 A(设为 \(k\))
\(f[i][j]\) 表示前 \(i\) 个数中选了 \(j\) 个 A。对每次枚举进行 DP。
时间复杂度 \(O(n^3)\)。
LNR R2 D1 T3 不等关系
把大于号变成(没有限制-小于号)。
考虑朴素容斥,对于只有小于号和没有限制的方案数是 \(\frac{(n+1)!}{\prod(p_i+1)!}\),\(p_i\) 是每段连续的小于号的长度。
太慢了。
\(f[i]\) 表示将前 \(i\) 个数分完段了。答案是 \(f[n](n+1)!\)。
枚举上一个选没有限制的位置 \(j\),\(f[i]=\sum f[j]\frac{1}{(i-j)!}(-1)^{s_i-s_j}\),\(s_i\) 表示前缀中大于号的个数。
可以分治 FFT 优化到 \(O(n\log^2n)\),多项式求逆优化到 \(O(n\log n)\)。
AGC035F Two Histograms
掉线……
CTS 2019 D1T1 随机立方体
求概率和求方案数没什么区别。
三维比较复杂,先考虑二维,是类似的。
二项式反演,计算至少 \(k\) 个极大的数的方案数会更好做。
首先每行每列都至多只有一个数是极大的。
不妨把这 \(k\) 个极大的数放到主对角线的左上,这样好考虑。只要保证这 \(k\) 个极大,剩下的都随便放。
同时,这 \(k\) 个极大的数从左上到右下是递减的。
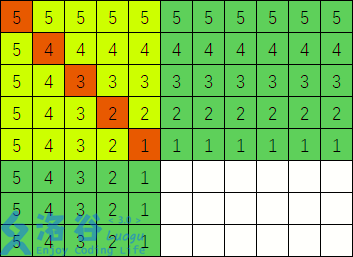
比如上图这样。(图片来源:兔队)
选出这 \(k\) 个极大数有 \(n^\underline{k}m^\underline{k}\) 种选择(要考虑顺序,也就是大小关系)。
对于红色部分,每个点都要小于左上的点。
对于黄绿色部分,每个点都要小于和它同一行和同一列的红点。由于红点已经有大小关系,所以让主对角线左下的点小于它右面的红点,右上的点小于它下面的红点就行了。
对于绿色部分,也是小于与它同一行或者同一列的红点。
对于白色部分,没有限制。
把大小关系连成一个森林。
有结论:给一个 \(n\) 个点的有根树森林赋点权,赋成 \(1\) 到 \(n\) 的排列,那么这棵森林中都是“堆”的方案数是 \(\frac{n!}{\prod size_u}\)。应该很好理解,从浅往深考虑,把最大的要放到这棵子树的根处,在 \(size_u!\) 种方案中有 \((size_u-1)!\) 种。
所以这里的方案数就是 \(\frac{(nm)!}{\prod\limits_{i=1}^k(nm-(n-i)(m-i))}\)。
三维也差不多。所以至少 \(k\) 个极大点的方案数是 \(n^\underline{k}m^\underline{k}l^\underline{k}\frac{(nml)!}{\prod\limits_{i=1}^k(nml-(n-i)(m-i)(l-i))}\)。由于要求期望,把分子上的 \((nml)!\) 丢掉就行了。
二项式反演一波走人。时间复杂度可以做到 \(O(\min(n,m,l))\)。
Endless Spin
长度为 \(n\) 的区间,每次随机一段染黑,问期望多少次全部染黑。
\(n\le 100\)
直接 min-max 容斥。
染不到第 \(i\) 块的概率是 \(\frac{i(i+1)+(n-i+1)(n-i+2)}{n(n+1)}\)。
\(f[i][j][k]\) 表示考虑前 \(i\) 个位置,当前最后一段区间长 \(k\),总的选法(上面的分子)为 \(j\)。
如果下一个不选,可以转移到 \(f[i+1][j+k+1][k+1]\)。
如果下一个选,可以转移到 \(f[i+1][j][0]\)。(要先乘上系数 \(-1\))
答案是 \(\sum\limits_{j=0}^{\binom{n+1}{2}-1}\frac{f[n][j][k]}{1-\frac{j}{\binom{n+1}{2}}}\)。
(还是不懂……)
Random Graph
给 \(n\) 个点的图,一开始没有边,每次随机两个点,然后连边。可能会随机到自环和重边。
问期望多长时间联通。
\(n\le 100\)
\(n\) 个点 \(m\) 条边的连通图个数怎么算?
考虑求不连通的图个数,枚举 \(1\) 所在的连通块的点数和边数。
概率呢?\(n\) 个点 \(m\) 条边的连通概率。
令 \(h[n][m]=1-g[n][m]\),也就是不连通概率。
答案就是 \(\sum h[n][m]\)。
下证 \(g[n][m]\) 可以表示成 \(\sum\limits_{i=0}^{n^2}C_{n,i}(\frac{i}{n^2})^m\)。其中 \(C_{n,i}\) 是某些常数。
证明不难。并且可以证明 \(C_{n,n^2}=1\)。
那么答案是 \(\sum\limits_{m\ge 0}(-\sum\limits_{i=0}^{n^2-1}C_{n,i}(\frac{i}{n^2})^m)=\sum\limits_{i=0}^{2n-1}-C_{n,i}\sum\limits_{m\ge 0}(\frac{i}{n^2})^m\)。
怎么求 \(C_{n,i}\)?
掉线了,以后再说。
LGV 引理
在一个 DAG 上,如果有一些起点 \(a_i\),一些终点 \(b_i\),如果在 \(a_i\rightarrow b_j,a_k\rightarrow b_l\) 相交时必有 \(i<k,j>l\),那么不相交的路径条数为 \(\det(g(i,j))\),\(g(i,j)\) 表示 \(a_i\) 到 \(b_j\) 的路径条数。
某经典题
\(n\times m\) 的矩阵中,填 \(1\) 到 \(k\),要求每个数都要 \(\ge\) 右边的数和下面的数,问多少种方案。
考虑画出每种数的轮廓线。这些轮廓线必不相交(可能部分或全部重合)。
反过来,没有交点的轮廓线一定可以对应一种矩阵。
LGV 引理一下即可。
EI 与菱形计数
想象成是一个立体图,\(a\times b\) 的矩阵,每个上面可以堆立方体,至多 \(c\) 个。
然后就变成上面的经典题了。
那个行列式也可以推出来是个很简洁的东西。
(具体去讨论看吧)

