[BJOI2019]勘破神机(第一类斯特林数,斐波那契数列)
真的是好题,只不过强行多合一有点过分了……
题目大意:
$T$ 组数据。每个测试点中 $m$ 相同。
对于每组数据,给定 $l,r,k$,请求出 $\dfrac{1}{r-l+1}\sum\limits_{n=l}^r\dbinom{f(n,m)}{k}\bmod 998244353$。
其中 $f(n,m)$ 表示用 $1\times 2$ 的骨牌(可以变成 $2\times 1$)填满 $n\times m$ 的网格的方案数。
$1\le T\le 5,1\le l\le r\le 10^{18},1\le k\le 501,2\le m\le 3$。保证 $r-l+1$ 不是 $998244353$ 的倍数。
$2\le m\le 3$,明显二合一了。(其实后面会发现不止二合一)
先看 $m=2$。众所周知 $f(n,2)=fib_{n+1}$。然后就变成这题了。注意 $\sqrt{5}$ 在模 $998244353$ 下也没有意义,还是要扩系。
接下来看 $m=3$。
首先肯定 $n$ 是偶数的时候 $f(n,3)$ 才不为 $0$,那么设 $g_n=f(2n,3)$,然后要求就是 $\sum\limits_{n=\lceil\frac{l}{2}\rceil}^{\lfloor\frac{r}{2}\rfloor}g_n$。(为方便下文假设求 $l$ 到 $r$ 的和)
(从题解偷张图,%%%vixbob)
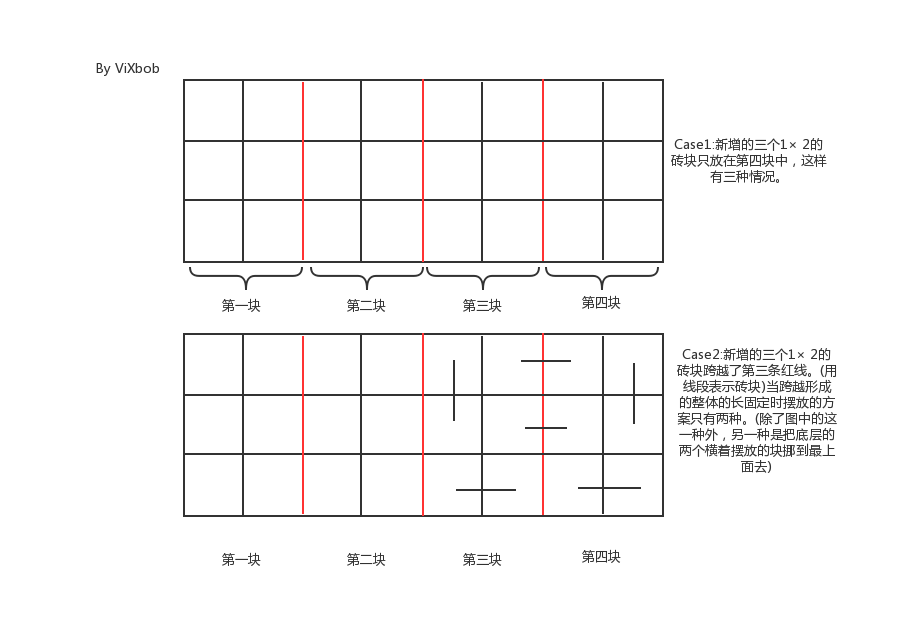
说得应该很清楚了。那么 $g_n=3g_{n-1}+2\sum\limits_{i=0}^{n-2}g_i$。
那么 $g_{n+1}-g_n=3g_n-g_{n-1}$,得递推公式 $g_n=4g_{n-1}-g_{n-2}$。初始 $g_0=1,g_1=3$。
用特征方程解出通项公式:
$$g_n=\dfrac{3+\sqrt{3}}{6}(2+\sqrt{3})^n+\dfrac{3-\sqrt{3}}{6}(2-\sqrt{3})^n$$
然后就一样了。
时间复杂度 $O(Tk^2\log r)$。

#include<bits/stdc++.h> using namespace std; typedef long long ll; const int maxn=555,mod=998244353,inv2=499122177,inv5=598946612,inv6=166374059; #define FOR(i,a,b) for(int i=(a);i<=(b);i++) #define ROF(i,a,b) for(int i=(a);i>=(b);i--) #define MEM(x,v) memset(x,v,sizeof(x)) inline ll read(){ char ch=getchar();ll x=0,f=0; while(ch<'0' || ch>'9') f|=ch=='-',ch=getchar(); while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar(); return f?-x:x; } int t,m,k,fac[maxn],invfac[maxn],S[maxn][maxn],C[maxn][maxn]; ll l,r; inline int add(int x,int y){return x+y<mod?x+y:x+y-mod;} inline int sub(int x,int y){return x<y?x-y+mod:x-y;} inline int mul(int x,int y){return 1ll*x*y%mod;} inline int qpow(int a,ll b){ int ans=1; for(;b;b>>=1,a=mul(a,a)) if(b&1) ans=mul(ans,a); return ans; } template<int T> struct comp{ int x,y; comp(const int xx=0,const int yy=0):x(xx),y(yy){} inline comp operator+(const comp &c)const{return comp(add(x,c.x),add(y,c.y));} inline comp operator-(const comp &c)const{return comp(sub(x,c.x),sub(y,c.y));} inline comp operator*(const comp &c)const{return comp(add(mul(x,c.x),mul(T,mul(y,c.y))),add(mul(x,c.y),mul(y,c.x)));} inline comp inv()const{ comp ans(x,y?mod-y:0); int dn=qpow(sub(mul(x,x),mul(T,mul(y,y))),mod-2); return ans*dn; } inline comp operator/(const comp &c)const{return *this*c.inv();} inline bool operator==(const comp &c)const{return x==c.x && y==c.y;} }; comp<5> a2(0,inv5),b2(0,mod-inv5),x2(inv2,inv2),y2(inv2,mod-inv2); comp<3> a3(inv2,inv6),b3(inv2,mod-inv6),x3(2,1),y3(2,mod-1); template<int T> inline comp<T> cqpow(comp<T> a,ll b){ comp<T> ans(1,0); for(;b;b>>=1,a=a*a) if(b&1) ans=ans*a; return ans; } template<int T> comp<T> calc(comp<T> x,ll l,ll r){ if(x==1) return (r-l+1)%mod; return (cqpow(x,r+1)-cqpow(x,l))/(x-1); } int main(){ FOR(i,0,501) C[i][0]=C[i][i]=1; FOR(i,1,501) FOR(j,1,i-1) C[i][j]=add(C[i-1][j],C[i-1][j-1]); S[1][1]=1; FOR(i,2,501) FOR(j,1,i) S[i][j]=add(mul(i-1,S[i-1][j]),S[i-1][j-1]); fac[0]=1; FOR(i,1,501) fac[i]=mul(fac[i-1],i); invfac[501]=qpow(fac[501],mod-2); ROF(i,500,0) invfac[i]=mul(invfac[i+1],i+1); t=read();m=read(); while(t--){ l=read();r=read();k=read(); if(m==2){ int ans=0; FOR(i,0,k){ int s=0; FOR(j,0,i){ comp<5> tmp1=cqpow(a2,j)*cqpow(b2,i-j),tmp2=cqpow(x2,j)*cqpow(y2,i-j); s=add(s,mul(C[i][j],(tmp1*calc(tmp2,l+1,r+1)).x)); } s=mul(s,S[k][i]); if((k-i)&1) ans=sub(ans,s); else ans=add(ans,s); } printf("%d\n",mul(mul(ans,invfac[k]),qpow((r-l+1)%mod,mod-2))); } else{ ll lll=(l+1)>>1,rrr=r>>1; if(lll>rrr){puts("0");continue;} int ans=0; FOR(i,0,k){ int s=0; FOR(j,0,i){ comp<3> tmp1=cqpow(a3,j)*cqpow(b3,i-j),tmp2=cqpow(x3,j)*cqpow(y3,i-j); s=add(s,mul(C[i][j],(tmp1*calc(tmp2,lll,rrr)).x)); } s=mul(s,S[k][i]); if((k-i)&1) ans=sub(ans,s); else ans=add(ans,s); } printf("%d\n",mul(mul(ans,invfac[k]),qpow((r-l+1)%mod,mod-2))); } } }




