RNN+LSTM
一、RNN
RNN的时间顺序展开图:

RNN的节点内部结构:
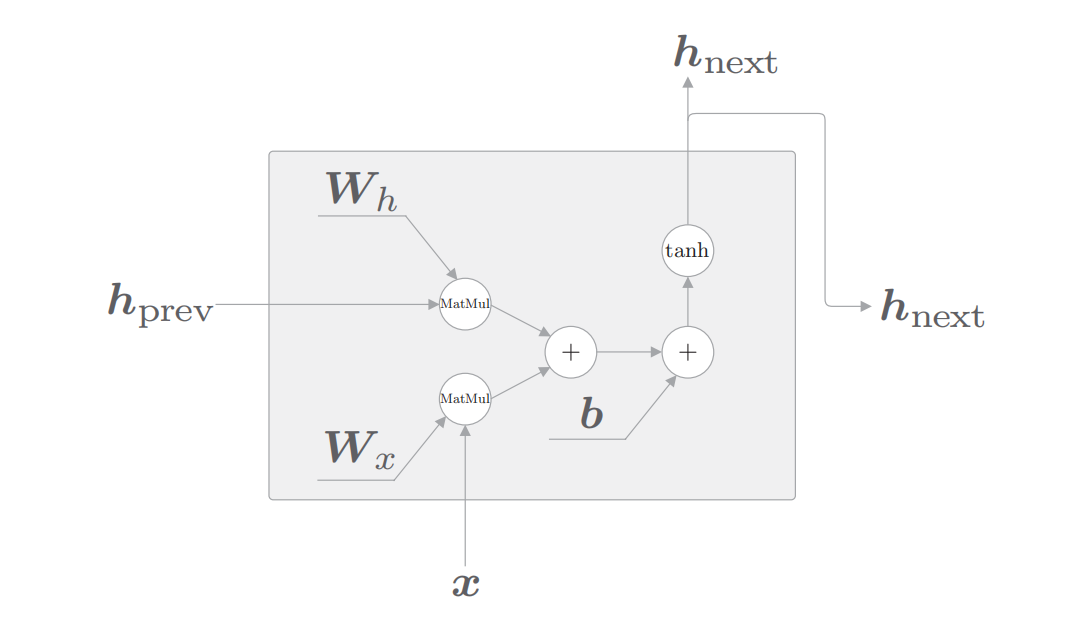
其中'MatMul'代表矩阵相乘,'+'代表矩阵相加,'tanh'代表对应的激活函数。Wh为隐状态矩阵,Wx为权重矩阵,其中hprev和x为输入,hnext为输出。公式如下:
$$
\boldsymbol{h}_{next}=\tanh \left(\boldsymbol{h}_{prev} \boldsymbol{W}_{h}+\boldsymbol{x}_{next} \boldsymbol{W}_{x}+\boldsymbol{b}\right)
$$
二、LSTM

如图所示, LSTM 与 RNN 的接口的不同之处在于,LSTM 还有 路径 $\boldsymbol{c}_{\circ}$ 这个 $\boldsymbol{c}$ 称为记忆单元 (或者简称为 “单元” ), 相当于 LSTM 专用 的记忆部门。
记忆单元的特点是, 仅在 LSTM 层内部接收和传递数据。也就是说, 记忆单元在 LSTM 层内部结束工作,不向其他层输出。而 LSTM 的隐藏状 态 $\boldsymbol{h}$ 和 $\mathrm{RNN}$ 层相同, 会被(向上)输出到其他层。
$\tanh$ 的输出是 $-1.0 \sim 1.0$ 的实数。我们可以认为这个 $-1.0 \sim 1.0$ 的 数值表示某种被编码的 “信息” 的强弱 (程度)。而 sigmoid 函数的 输出是 $0.0 \sim 1.0$ 的实数, 表示数据流出的比例。因此, 在大多数情 况下, 门使用 sigmoid 函数作为激活函数, 而包含实质信息的数据 则使用 $\tanh$ 函数作为激活函数。
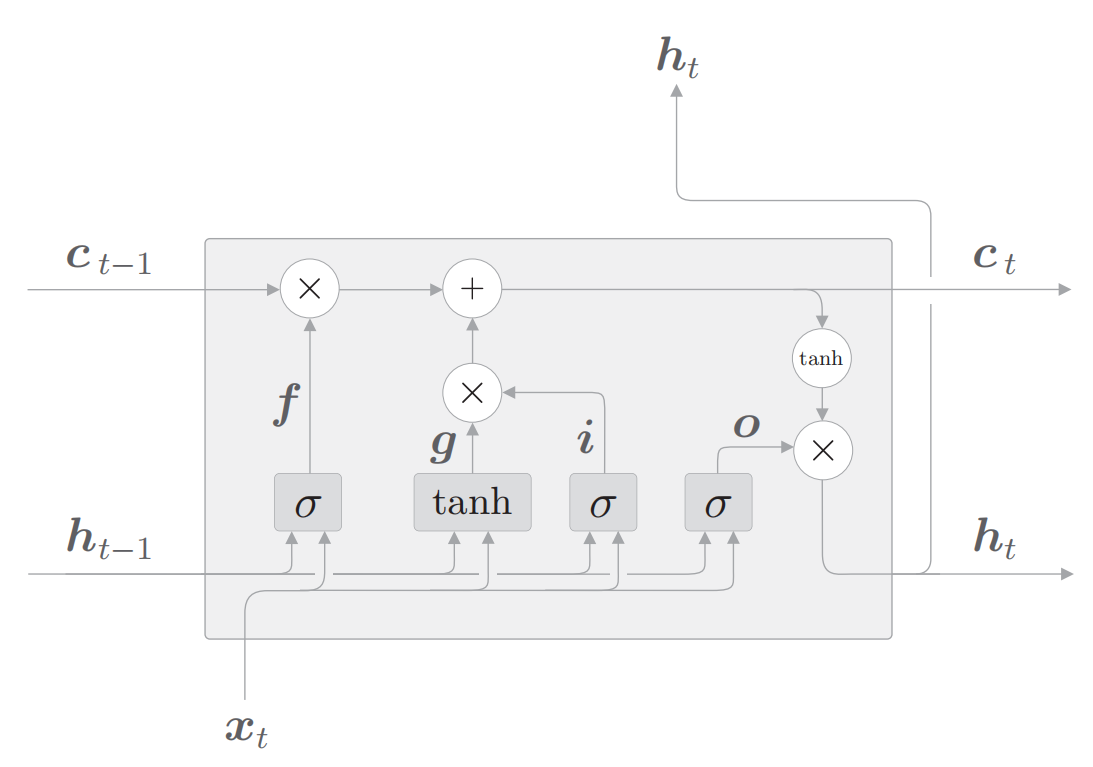
下图为LSTM内部结构图:
$$
\begin{gathered}
\boldsymbol{f}=\sigma\left(\boldsymbol{x}_{t} \boldsymbol{W}_{x}^{(\mathrm{f})}+\boldsymbol{h}_{t-1} \boldsymbol{W}_{h}^{(\mathrm{f})}+\boldsymbol{b}^{(\mathrm{f})}\right) \\
\boldsymbol{g}=\tanh \left(\boldsymbol{x}_{t} \boldsymbol{W}_{x}^{(\mathrm{g})}+\boldsymbol{h}_{t-1} \boldsymbol{W}_{h}^{(\mathrm{g})}+\boldsymbol{b}^{(\mathrm{g})}\right) \\
\boldsymbol{i}=\sigma\left(\boldsymbol{x}_{t} \boldsymbol{W}_{x}^{(\mathrm{i})}+\boldsymbol{h}_{t-1} \boldsymbol{W}_{h}^{(\mathrm{i})}+\boldsymbol{b}^{(\mathrm{i})}\right) \\
\boldsymbol{o}=\sigma\left(\boldsymbol{x}_{t} \boldsymbol{W}_{x}^{(\mathrm{o})}+\boldsymbol{h}_{t-1} \boldsymbol{W}_{h}^{(\mathrm{o})}+\boldsymbol{b}^{(\mathrm{o})}\right) \\
\boldsymbol{c}_{t}=\boldsymbol{f} \odot \boldsymbol{c}_{t-1}+\boldsymbol{g} \odot i \\
\boldsymbol{h}_{t}=\boldsymbol{o} \odot \tanh \left(\boldsymbol{c}_{t}\right)
\end{gathered}
$$
提示:图中的灰色矩形代表缩略图,真正代表仿射变换(指在几何中,一个向量空间进行一次线性变换并接上一个平移,变换为另一个向量空间),图中的'X'和公式中的'$\odot$'代表矩阵元素相乘(阿达玛积)。
LSTM难以产生梯度消失和梯度爆炸的原因
我们仅关注记忆单元, 此时, 记 忆单元的反向传播仅流过 “$+$" 和 “ $x$ ” 节点。“+”节点将上游传来的梯度 原样流出, 所以梯度没有变化 (退化)。而 “ $x$ ” 节点的计算并不是矩阵乘积, 而是对应元素的乘积 ( 阿达玛 积 $)$ 。顺便说一下, 在之前的 $\mathrm{RNN}$ 的反向传播中, 我们使用相同的权重矩 阵重复了多次矩阵乘积计算, 由此导致了梯度消失 (或梯度爆炸 )。而这里 的 LSTM 的反向传播进行的不是矩阵乘积计算, 而是对应元素的乘积计算, 而且每次都会基于不同的门值进行对应元素的乘积计算。这就是它不会发生 梯度消失(或梯度爆炸)的原因。
Cnext到Cprev的 “ $x$ ” 节点的计算由遗忘门控制 (每次输出不同的门值)。遗忘 门认为 “应该忘记” 的记忆单元的元素, 其梯度会变小; 而遗忘门认为 “不能 忘记” 的元素, 其梯度在向过去的方向流动时不会退化。因此, 可以期待记忆 单元的梯度 (应该长期记住的信息) 能在不发生梯度消失的情况下传播。
整合 4 个权重进行仿射变换的 LSTM的计算图:

如图所示, 先一起执行 4 个仿射变换。然后, 基于 slice 节点, 取 出 4 个结果。这个 slice 节点很简单, 它将仿射变换的结果 (矩阵 ) 均等地 分成 4 份, 然后取出内容。在 slice 节点之后, 数据流过激活函数 ( sigmoid 函数或 $\tanh$ 函数 $)$, 进行计算。
参考:
《深度学习进阶:自然语言处理》


