反向传播算法之梯度下降

一、导数常见性质

1.基本函数的导数

• 常数函数c导数为0，如y=2函数的导数为$\frac{\mathrm{d} y}{\mathrm{d} x} $ = 0

• 线性函数y = ax + c 导数为a，如函数y = 2x + 1导数$\frac{\mathrm{d} y}{\mathrm{d} x}$ = 2

• 幂函数$x^{a}$ 导数为$ax^{a-1}$，如y = $x^{2}$函数$\frac{\mathrm{d} y}{\mathrm{d} x}$ = 2x

• 指数函数$a^{x}$ 导数为$a^{x}ln_{}a$，如y = $e^{x}$函数$\frac{\mathrm{d} y}{\mathrm{d} x}$ = $e^{x}$

• 对数函数$log_{a} x$ 导数为$\frac{1}{xln_{} a}$，如y = $ln_{}x$函数$\frac{\mathrm{d} y}{\mathrm{d} x}$ = $\frac{1}{xln_{} e}$ = $\frac{1}{x}$

2.常用导数性质

• 函数加减$(f+g)^{\prime}=f^{\prime}+g^{\prime}$
• 函数相乘$(f g)^{\prime}=f^{\prime} \cdot g+f \cdot g^{\prime}$
• 函数相除$\left(\frac{f}{g}\right)^{\prime}=\frac{f^{\prime} g-f g^{\prime}}{g^{2}}, \quad g \neq 0$
• 复合函数的导数，考虑复合函数$f(g(x))$，令$u=g(x)$，其导数为：$\frac{\mathrm{d} f(g(x))}{\mathrm{d} x}=\frac{\mathrm{d} f(u)}{\mathrm{d} u} \frac{\mathrm{d} g(x)}{\mathrm{d} x}=f^{\prime}(u) \cdot g^{\prime}(x)$

二、关于梯度

1.链式求导

若多元函数 u=g(y₁,y₂,...,y_m) 在点 𝒃=(b₁,b₂,...,b_m) 处可微，b_i=f_i(a₁,a₂,...,a_n)(i=1,2,...,m)，每个函数 f_i(x₁,x₂,...,x_n) 在点 (a₁,a₂,...,a_n) 处都可微，则函数 u=g(f₁(x₁,x₂,...,x_n)，f₂(x₁,x₂,...,x_n),...,f_m(x₁,x₂,...,x_n)) 也在(a₁,a₂,...,a_n) 处可微，且

$\frac{\partial u}{\partial x_{j}}=\sum_{i=1}^{m} \frac{\partial g}{\partial y_{i}} \bullet \frac{\partial y_{i}}{\partial x_{j}}$ = $\sum_{i=1}^{m} \frac{\partial g}{\partial y_{i}} \cdot \frac{\partial f_{i}}{\partial x_{j}}(j=1,2, \cdots, n)$

这就是多元函数的链式法则。

2.偏导数

在数学中，偏导数（英语：partial derivative）的定义是：一个多变量的函数(或称多元函数)，对其中一个变量(导数)微分，而保持其他变量恒定（相对于全导数，在其中所有变量都允许变化）。
函数${\displaystyle f}$关于变量${\displaystyle x}$的偏导数写为${\displaystyle f_{x}^{\prime }}$或${\displaystyle {\frac {\partial f}{\partial x}}}$。

3.方向导数

方向导数为函数在某一个方向上的导数，具体地，定义 $x y$ 平面上一点 $(a, b)$ 以及单位向量 $\vec{u}=(\cos \theta, \sin \theta)$ ，在曲 面 $z=f(x, y)$ 上，从点 $(a, b, f(a, b))$ 出发, 沿 $\vec{u}=(\cos \theta, \sin \theta)$ 方向走 $t$ 单位长度后，函数值 $z$ 为 $F(t)=f(a+t \cos \theta, b+t \sin \theta)$, 则点 $(a, b)$ 处 $\vec{u}=(\cos \theta, \sin \theta)$ 方向的方向导数为 :

$\left.\frac{d}{d t} f(a+t \cos \theta, b+t \sin \theta)\right|_{t=0}$

=$\lim _{t \rightarrow 0} \frac{f(a+t \cos \theta, b+t \sin \theta)-f(a, b)}{t}$

=$\lim _{t \rightarrow 0} \frac{f(a+t \cos \theta, b+t \sin \theta)-f(a, b+t \sin \theta)}{t}+\lim _{t \rightarrow 0} \frac{f(a, b+t \sin \theta)-f(a, b)}{t}$

=$\frac{\partial}{\partial x} f(a, b) \frac{d x}{d t}+\frac{\partial}{\partial y} f(a, b) \frac{d y}{d t}$

=$f_{x}(a, b) \cos \theta+f_{y}(a, b) \sin \theta$

=$\left(f_{x}(a, b), f_{y}(a, b)\right) \cdot(\cos \theta, \sin \theta)$

上面推导中使用了链式法则。其中, $f_{x}(a, b)$ 和 $f_{y}(a, b)$ 分别为函数在 $(a, b)$ 位置的偏导数。由上面的推导可知： 该位置处，任意方向的方向导数为偏导数的线性组合，系数为该方向的单位向量。当该方向与坐标轴正方向一致 时，方向导数即偏导数，换句话说， 偏导数为坐标轴方向上的方向导数，其他方向的方向导数为偏导数的合成。 写成向量形式，偏导数构成的向量为 $\nabla f(a, b)=\left(f_{x}(a, b), f_{y}(a, b)\right)$, 称之为梯度。

4.梯度

梯度，写作 $\nabla f$, 二元时为 $\left(\frac{\partial z}{\partial x}, \frac{\partial z}{\partial y}\right)$, 多元时为 $\left(\frac{\partial z}{\partial x}, \frac{\partial z}{\partial y}, \ldots\right)$ 。

我们继续上面方向导数的推导， $(a, b)$ 处 $\theta$ 方向上的方向导数为

$\left(f_{x}(a, b), f_{y}(a, b)\right) \cdot(\cos \theta, \sin \theta)$

=$\mid\left(\left(f_{x}(a, b), f_{y}(a, b)\right)|\cdot| 1 \mid \cdot \cos \phi\right.$

=$|\nabla f(a, b)| \cdot \cos \phi$

其中, $\phi$ 为 $\nabla f(a, b)$ 与 $\vec{u}$ 的夹角，显然，当 $\phi=0$ 即 $\vec{u}$ 与梯㲥 $\nabla f(a, b)$ 同向时，方向导数取得最大值， 最大值为梯 度的模 $|\nabla f(a, b)|$, 当 $\phi=\pi$ 即 $\vec{u}$ 与梯庠 $\nabla f(a, b)$ 反向时，方向导数取得最小值，最小值为梯度模的相反数。此 外，根据上面方向导数的公式可知，在夹角 $\phi<\frac{\pi}{2}$ 时方向导数为正，表示 $\vec{u}$ 方向函数值上升， $\phi>\frac{\pi}{2}$ 时方向导数为 负，表示该方向函数值下降。

至此，方才有了梯度的几何意义：
1. 当前位置的梯度方向，为函数在该位置处方向导数最大的方向，也是函数值 上升最快的方向，反方向为下降最快的 方向;
2. 当前位置的梯度长度 (模)，为最大方向导数的值。

三、深度学习中的梯度下降算法

1.激活函数的求导

Sigmoid函数表达式：

$\sigma(x)=\frac{1}{1+e^{-x}}$

导数表达式：

$\frac{\mathrm{d}}{\mathrm{d} x} \sigma(x)=\frac{\mathrm{d}}{\mathrm{d} x}\left(\frac{1}{1+e^{-x}}\right)$

$=\frac{\mathrm{e}^{-x}}{\left(1+\mathrm{e}^{-x}\right)^{2}}$

$=\frac{\left(1+e^{-x}\right)-1}{\left(1+e^{-x}\right)^{2}}$

$=\frac{1+e^{-x}}{\left(1+e^{-x}\right)^{2}}-\left(\frac{1}{1+e^{-x}}\right)^{2}$

$=\sigma(x)-\sigma(x)^{2}$

$=\sigma(1-\sigma)$

可以看到, Sigmoid 函数的导数表达式最终可以表达为激活函数的输出值的简单运算, 利用这一性质, 在神经网络的梯度计算中, 通过缓存每层的 Sigmoid 函数输出值, 即可在需要的时候计算出其导数。Sigmoid 函数的导数曲线如图所示。

---

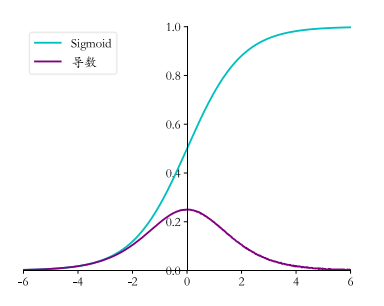
ReLU函数表达式：

$\operatorname{ReLU}(x)=\max (0, x)$

导数表达式：

$\frac{\mathrm{d}}{\mathrm{d} x} \operatorname{ReLU}= \begin{cases}1 & x \geq 0 \\ 0 & x<0\end{cases}$

可以看到, ReLU函数的导数计算简单, $x$ 大于等于零的时候, 导数值恒为 1 , 在反向传播 过程中, 它既不会放大梯度, 造成梯度爆炸(Gradient exploding)现象; 也不会缩小梯度, 造成梯度弥散(Gradient vanishing)现象。ReLU函数的导数曲线如图所示。

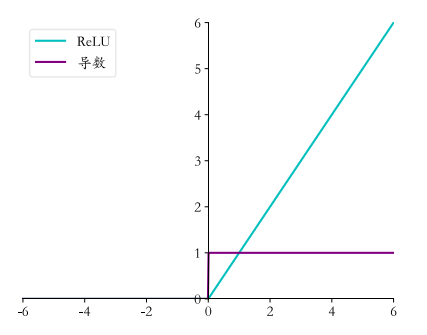
在 ReLU 函数被广泛应用之前, 神经网络中激活函数采用 Sigmoid 居多, 但是 Sigmoid 函数容易出现梯度弥散现象, 当网络的层数增加后, 较前层的参数由于梯度值非常微小, 参数长时间得不到有效更新, 无法训练较深层的神经网络, 导致神经网络的研究一直停留 在浅层。随着 ReLU 函数的提出, 很好地缓解了梯度弥散的现象, 神经网络的层数能够地 达到较深层数, 如 AlexNet 中采用了 ReLU 激活函数, 层数达到了 8 层, 后续提出的上百 层的卷积神经网络也多是采用 $\operatorname{ReLU}$ 激活函数。

---

Tanh函数表达式：

$\tanh (x)=\frac{\left(e^{x}-e^{-x}\right)}{\left(e^{x}+e^{-x}\right)}$

$=2 \cdot \operatorname{sigmoid}(2 x)-1$

导数表达式：

$\frac{\mathrm{d}}{\mathrm{d} x} \tanh (x)=\frac{\left(e^{x}+e^{-x}\right)\left(e^{x}+e^{-x}\right)-\left(e^{x}-e^{-x}\right)\left(e^{x}-e^{-x}\right)}{\left(e^{x}+e^{-x}\right)^{2}}$

$=1-\frac{\left(e^{x}-e^{-x}\right)^{2}}{\left(e^{x}+e^{-x}\right)^{2}}=1-\tanh ^{2}(x)$

tanh 函数及其导数曲线如图所示。

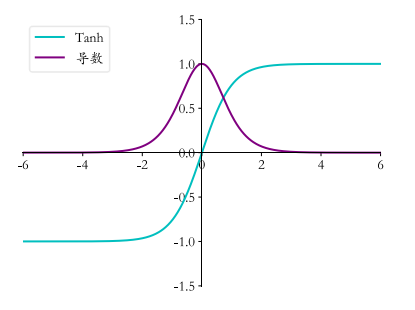
2.损失函数的梯度

均方误差损失函数(MSE)表达式：

$\mathcal{L}=\frac{1}{2} \sum_{k=1}^{K}\left(y_{k}-o_{k}\right)^{2}$

其中$y$表示真实标签值$o$表示神经网络最后一层的输出。上式中的 $\frac{1}{2}$ 项用于简化计算, 也可以利用 $\frac{1}{K}$ 进行平均, 这些缩放运算均不会改变梯度方向。 则它的偏导数 $\frac{\partial \mathcal{L}}{\partial o_{i}}$ 可以展开为:

$\frac{\partial \mathcal{L}}{\partial o_{i}}=\frac{1}{2} \sum_{k=1}^{K} \frac{\partial}{\partial o_{i}}\left(y_{k}-o_{k}\right)^{2}$

利用复合函数导数法则分解为:

$\frac{\partial \mathcal{L}}{\partial o_{i}}=\frac{1}{2} \sum_{k=1}^{K} 2 \cdot\left(y_{k}-o_{k}\right) \cdot \frac{\partial\left(y_{k}-o_{k}\right)}{\partial o_{i}}$

即

$\frac{\partial \mathcal{L}}{\partial o_{i}}=\sum_{k=1}^{K}\left(y_{k}-o_{k}\right) \cdot-1 \cdot \frac{\partial o_{k}}{\partial o_{i}}$

$=\sum_{k=1}^{K}\left(o_{k}-y_{k}\right) \cdot \frac{\partial o_{k}}{\partial o_{i}}$

考虑到 $\frac{\partial o_{k}}{\partial o_{i}}$ 仅当 $k=i$ 时才为 1 , 其它点都为 0 , 也就是说, 偏导数 $\frac{\partial L_{i}}{\partial_{i}}$ 只与第 $i$ 号节点相关, 与 其它节点无关, 因此上式中的求和符号可以去掉。均方误差函数的导数可以推导为:

$\frac{\partial \mathcal{L}}{\partial o_{i}}=\left(o_{i}-y_{i}\right)$

---

在计算交叉熵损失函数时, 一般将 Softmax 函数（Softmax为激活函数，用于神经网络计算损失之前）与交叉熵函数统一实现。我们先推导 Softmax 函数的梯度, 再推导交叉熵函数的梯度。

Softmax函数表达式：

$p_{i}=\frac{e^{z_{i}}}{\sum_{k=1}^{K} e^{Z_{k}}}$

它的功能是将𝐾个输出节点的值转换为概率，并保证概率之和为1，如下图所示。

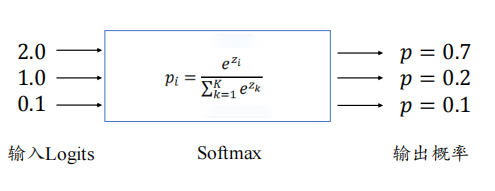
下面分为$i = j$和$i ≠ j$讨论偏导数求解情况。

1.$i = j$时

Softmax函数的偏导数可以展开为：

$\frac{\partial p_{i}}{\partial z_{j}}=\frac{\partial \frac{e^{z_{i}}}{\sum_{k=1}^{K} e^{z_{k}}}}{\partial z_{j}}=\frac{e^{z_{i}} \sum_{k=1}^{K} e^{z_{k}}-e^{z_{j}} e^{z_{i}}}{\left(\sum_{k=1}^{K} e^{z_{k}}\right)^{2}}$

提取公共项 $e^{z_{i}}$ :

$=\frac{e^{z_{i}}\left(\sum_{k=1}^{K} e^{z_{k}}-e^{z_{j}}\right)}{\left(\sum_{k=1}^{K} e^{z_{k}}\right)^{2}}$

拆分为两部分:

$=\frac{e^{z_{i}}}{\sum_{k=1}^{K} e^{z_{k}}} \times \frac{\left(\sum_{k=1}^{K} e^{z_{k}}-e^{z_{j}}\right)}{\sum_{k=1}^{K} e^{z_{k}}}$

可以看到, 上式是概率值 $p_{i}$ 和 $1-p_{j}$ 的相乘, 同时满足 $p_{i}=p_{j}$ 。 因此 $i=j$ 时, Softmax 函数 的偏导数 $\frac{\partial p_{i}}{\partial z_{j}}$ 为:

$\frac{\partial p_{i}}{\partial z_{j}}=p_{i}\left(1-p_{j}\right), i=j$

2.$i ≠ j$时

Softmax函数的偏导数可以展开为：

$\frac{\partial p_{i}}{\partial z_{j}}=\frac{\partial \frac{e^{z_{i}}}{\sum_{k=1}^{K} e^{z_{k}}}}{\partial z_{j}}=\frac{0-e^{z_{j}} e^{z_{i}}}{\left(\sum_{k=1}^{K} e^{z_{k}}\right)^{2}}$

去掉 0 项，并分解为两项相乘：

$=\frac{-e^{z_{j}}}{\sum_{k=1}^{K} e^{z_{k}}} \times \frac{e^{z_{i}}}{\sum_{k=1}^{K} e^{z_{k}}}$

即：

$\frac{\partial p_{i}}{\partial z_{j}}=-p_{j} \cdot p_{i}$

 

所以最终的Softmax表达式为：

$\frac{\partial p_{i}}{\partial z_{j}}= \begin{cases}p_{i}\left(1-p_{j}\right) & \text { 当 } i=j \\ -p_{i} \cdot p_{j} & \text { 当 } i \neq j\end{cases}$

---

交叉熵损失函数表达式：

$\mathcal{L}=-\sum_{k} y_{k} \log \left(p_{k}\right)$

这里直接来推导最终损失值 $L$ 对网络输出 $\operatorname{logits}$ 变量 $z_{i}$ 的偏导数, 展开为:

$\frac{\partial \mathcal{L}}{\partial z_{i}}=-\sum_{k} y_{k} \frac{\partial \log \left(p_{k}\right)}{\partial z_{i}}$

$=-\sum_{k} y_{k} \frac{\partial \log \left(p_{k}\right)}{\partial p_{k}} \cdot \frac{\partial p_{k}}{\partial z_{i}}$

即：

$=-\sum_{k} y_{k} \frac{1}{p_{k}} \cdot \frac{\partial p_{k}}{\partial z_{i}}$

其中 $\frac{\partial p_{k}}{\partial z_{i}}$ 即为我们已经推导的 Softmax 函数的偏导数。
将求和符号拆分为 $k=i$ 以及 $k \neq i$ 的两种情况, 并代入 $\frac{\partial p_{k}}{\partial z_{i}}$ 求解的公式, 可得

$\frac{\partial \mathcal{L}}{\partial z_{i}}=-y_{i}\left(1-p_{i}\right)-\sum_{k \neq i} y_{k} \frac{1}{p_{k}}\left(-p_{k} \cdot p_{i}\right)$

进一步化简为

$=-y_{i}\left(1-p_{i}\right)+\sum_{k \neq i} y_{k} \cdot p_{i}$

$=-y_{i}+y_{i} p_{i}+\sum_{k \neq i} y_{k} \cdot p_{i}$

提供公共项 $p_{i}$, 可得:

$\frac{\partial \mathcal{L}}{\partial z_{i}}=p_{i}\left(y_{i}+\sum_{k \neq i} y_{k}\right)-y_{i}$

特别地, 对于分类问题中标签 $y$ 通过 One-hot 编码的方式, 则有如下关系:

$\sum_{k} y_{k}=1$

$y_{i}+\sum_{k \neq i} y_{k}=1$

因此交叉熵的偏导数可以进一步简化为：

$\frac{\partial \mathcal{L}}{\partial z_{i}}=p_{i}-y_{i}$

3.全连接神经网络的反向传播算法

下面将以全连接层网络、激活函数采用 Sigmoid 函数、误差函数为 Softmax+MSE 损失函数的神经网络为例，推导其梯度传播规律。

对于采用 Sigmoid 激活函数的神经元模型，它的数学模型可以写为：

$o=\sigma\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b\right)$

假设有模型结构如下的三层神经网络，现在先对输出层K的梯度求解（求解过程均省略上标）

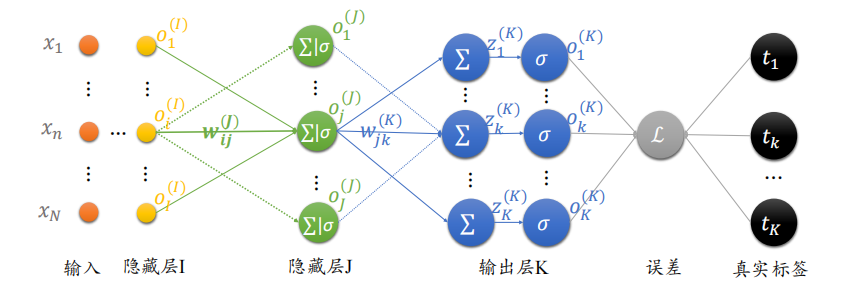
 w_{j \mathrm{k}}$ 是输入第j号节点与输出第 $k$ 号节点的连接权值。均方误差可以表达为:

$\mathcal{L}=\frac{1}{2} \sum_{i=1}^{K}\left(o_{i}-t_{i}\right)^{2}$

由于 $\frac{\partial \mathcal{L}}{\partial w_{j k}}$ 只与节点 $o_{k}$ 有关联, 上式中的求和符号可以去掉, 即 $i=k$ :

$\frac{\partial \mathcal{L}}{\partial w_{j k}}=\left(o_{k}-t_{k}\right) \frac{\partial o_{k}}{\partial w_{j k}}$

将 $o_{k}=\sigma\left(z_{k}\right)$ 代入可得:

$\frac{\partial \mathcal{L}}{\partial w_{j k}}=\left(o_{k}-t_{k}\right) \frac{\partial \sigma\left(z_{k}\right)}{\partial w_{j k}}$

考虑 Sigmoid 函数的导数 $\sigma^{\prime}=\sigma(1-\sigma)$, 代入可得:

$\frac{\partial \mathcal{L}}{\partial w_{j k}}=\left(o_{k}-t_{k}\right) \sigma\left(z_{k}\right)\left(1-\sigma\left(z_{k}\right)\right) \frac{\partial z_{k}}{\partial w_{j k}}$

将 $\sigma\left(z_{k}\right)$ 记为 $o_{k}$ :

$\frac{\partial \mathcal{L}}{\partial w_{j k}}=\left(o_{k}-t_{k}\right) o_{k}\left(1-o_{k}\right) \frac{\partial z_{k}}{\partial w_{j k}}$

将 $\frac{\partial z_{k}}{\partial w_{j k}}=o_{j}$ 替换, 最终可得:

$\frac{\partial \mathcal{L}}{\partial w_{j k}}=\left(o_{k}-t_{k}\right) o_{k}\left(1-o_{k}\right) o_{j}$

由此可以看到, 某条连接 $w_{j k}$ 上面的偏导数, 只与当前连接的输出节点 $o_{k}$, 对应的真实值 节点的标签 $t_{k}$, 以及对应的输入节点 $o_{j}$ 有关。

令 $\delta_{k}=\left(o_{k}-t_{k}\right) o_{k}\left(1-o_{k}\right)$, 则 $\frac{\partial \mathcal{L}}{\partial w_{j k}}$ 可以表达为:

$\frac{\partial \mathcal{L}}{\partial w_{j k}}=\delta_{k} x_{j}$

其中 $\delta_{k}$ 变量表征连接线的终止节点的误差梯度传播的某种特性, 使用 $\delta_{k}$ 表示后, $\frac{\partial L}{\partial w_{j k}}$ 偏导 数只与当前连接的起始节点 $x_{j}$, 终止节点处 $\delta_{k}$ 有关, 理解起来比较简洁直观。后续我们将 会在看到 $\delta_{k}$ 在循环推导梯度中的作用。

---

倒数第二层偏导表达式：

$\frac{\partial \mathcal{L}}{\partial w_{i j}}=\frac{\partial}{\partial w_{i j}} \frac{1}{2} \sum_{k}\left(o_{k}-t_{k}\right)^{2}$

由于 $\mathcal{L}$ 通过每个输出节点 $o_{k}$ 与 $w_{i j}$ 相关联, 故此处不能去掉求和符号, 运用链式法则将均方 差函数拆解：

$\frac{\partial \mathcal{L}}{\partial w_{i j}}=\sum_{k}\left(o_{k}-t_{k}\right) \frac{\partial}{\partial w_{i j}} o_{k}$

将 $o_{k}=\sigma\left(z_{k}\right)$ 代入可得:

$\frac{\partial \mathcal{L}}{\partial w_{i j}}=\sum_{k}\left(o_{k}-t_{k}\right) \frac{\partial}{\partial w_{i j}} \sigma\left(z_{k}\right)$

利用 Sigmoid 函数的导数 $\sigma^{\prime}=\sigma(1-\sigma)$ 进一步分解为:

$\frac{\partial \mathcal{L}}{\partial w_{i j}}=\sum_{k}\left(o_{k}-t_{k}\right) \sigma\left(z_{k}\right)\left(1-\sigma\left(z_{k}\right)\right) \frac{\partial z_{k}}{\partial w_{i j}}$

将 $\sigma\left(z_{k}\right)$ 写回 $o_{k}$ 形式, 并利用链式法则, 将 $\frac{\partial z_{k}}{\partial w_{i j}}$ 分解为:

$\frac{\partial \mathcal{L}}{\partial w_{i j}}=\sum_{k}\left(o_{k}-t_{k}\right) o_{k}\left(1-o_{k}\right) \frac{\partial z_{k}}{\partial o_{j}} \cdot \frac{\partial o_{j}}{\partial w_{i j}}$

其中 $\frac{\partial z_{k}}{\partial o_{j}}=w_{j k}$, 因此:

$\frac{\partial \mathcal{L}}{\partial w_{i j}}=\sum_{k}\left(o_{k}-t_{k}\right) o_{k}\left(1-o_{k}\right) w_{j k} \frac{\partial o_{j}}{\partial w_{i j}}$

考虑到 $\frac{\partial o_{j}}{\partial w_{i j}} k$ 无关, 可提取公共项为:

$\frac{\partial \mathcal{L}}{\partial w_{i j}}=\frac{\partial o_{j}}{\partial w_{i j}} \sum_{k}\left(o_{k}-t_{k}\right) o_{k}\left(1-o_{k}\right) w_{j k}$

进一步利用 $o_{j}=\sigma\left(z_{j}\right)$, 并利用 Sigmoid 导数 $\sigma^{\prime}=\sigma(1-\sigma)$, 将 $\frac{\partial o_{j}}{\partial w_{i j}}$ 拆分为:

$\frac{\partial \mathcal{L}}{\partial w_{i j}}=o_{j}\left(1-o_{j}\right) \frac{\partial z_{j}}{\partial w_{i j}} \sum_{k}\left(o_{k}-t_{k}\right) o_{k}\left(1-o_{k}\right) w_{j k}$

其中 $\frac{\partial z_{j}}{\partial w_{i j}}$ 的导数可直接推导出为 $o_{i}$, 上式可写为:

$\frac{\partial \mathcal{L}}{\partial w_{i j}}=o_{j}\left(1-o_{j}\right) o_{i} \sum_{k} \underbrace{\left(o_{k}-t_{k}\right) o_{k}\left(1-o_{k}\right)}_{\delta_{k}} w_{j k}$

其中 $\delta_{k}=\left(o_{k}-t_{k}\right) o_{k}\left(1-o_{k}\right)$, 则 $\frac{\partial L}{\partial w_{i j}}$ 的表达式可简写为:

$\frac{\partial \mathcal{L}}{\partial w_{i j}}=o_{j}\left(1-o_{j}\right) o_{i} \sum_{\mathrm{k}} \delta_{k} w_{j k}$

类似地, 仿照输出层 $\frac{\partial L}{\partial w_{j k}}=\delta_{k} x_{j}$ 的书写方式, 将 $\delta_{j}$ 定义为:

$\delta_{j} \triangleq o_{j}\left(1-o_{j}\right) \sum_{k} \delta_{k} w_{j k}$

此时 $\frac{\partial \mathcal{L}}{\partial w_{i j}}$ 可以写为当前连接的起始节点的输出值 $o_{i}$ 与终止节点 $j$ 的梯度变量信息 $\delta_{j}$ 的简单相 乘运算:

$\frac{\partial \mathcal{L}}{\partial w_{i j}}=\delta_{j} o_{i}$

可以看到, 通过定义 $\delta$ 变量, 每一层的梯度表达式变得更加清晣简洁, 其中 $\delta$ 可以简单 理解为当前连接 $w_{i j}$ 对误差函数的贡献值。

倒数第三层推导省略。

总结：

输出层：

$\frac{\partial \mathcal{L}}{\partial w_{j k}}=\delta_{k} o_{j}$

$\delta_{k}=o_{k}\left(1-o_{k}\right)\left(o_{k}-t_{k}\right)$

倒数第二层：

$\frac{\partial \mathcal{L}}{\partial w_{i j}}=\delta_{j} o_{i}$

$\delta_{j}=o_{j}\left(1-o_{j}\right) \sum_{k} \delta_{k} w_{j k}$

倒数第三层：

$\frac{\partial \mathcal{L}}{\partial w_{n i}}=\delta_{i} o_{n}$

$\delta_{i}=o_{i}\left(1-o_{i}\right) \sum_{j} \delta_{j} w_{i j}$

其实倒数第二层和倒数第三层并没有明显的变化。$o_{n}$为倒数第三层的输入，也可以拓展为倒数第四层的输出或是此处的$x_{n}$。

参考：

《TensorFlow深度学习》第七章全章

https://www.cnblogs.com/shine-lee/p/11715033.html

https://www.bilibili.com/video/BV1Zg411T71b?spm_id_from=333.999.0.0

https://zhuanlan.zhihu.com/p/149186719