BUUCTF之[SUCTF2019]SignIn(RE)

题目链接：https://buuoj.cn/challenges#[SUCTF2019]SignIn

 下载后是一个elf文件，先查壳，无壳

上IDA，进入main函数里面，f5

 

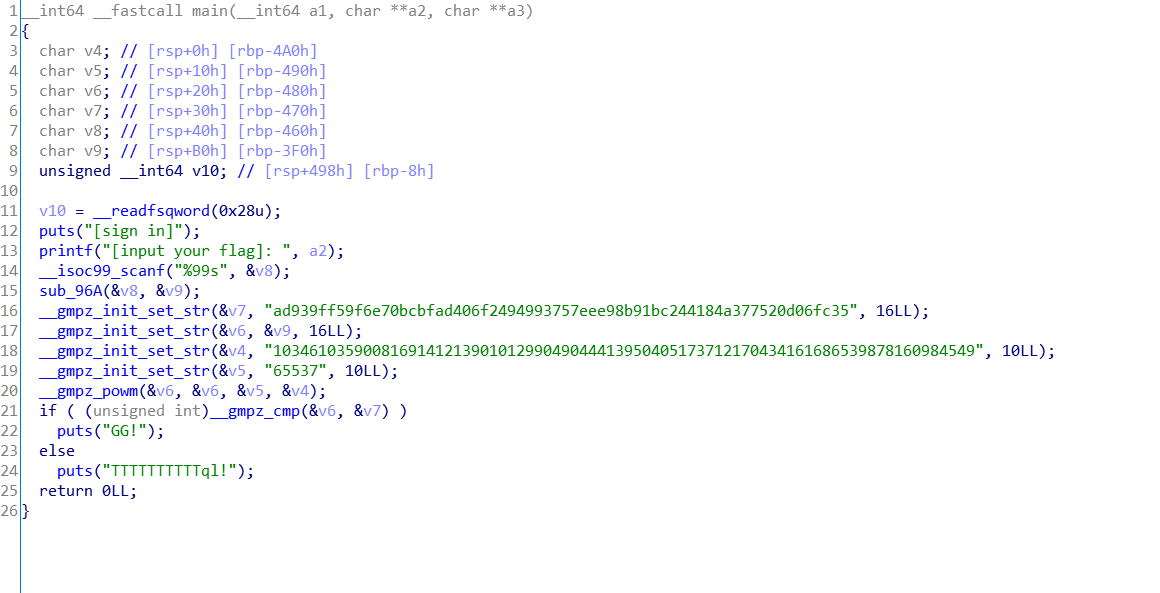
先看sub_96A，猜测一下，应该是转换这样的操作，这里我看了一下大佬们的解答，是十六进制转ascll，

 

 

继续往下看，程序调用了 __gmpz_init_set_str 函数，经过 Google 之后得知这其实是一个 GNU 高精度算法库(GNU Multiple Precision Arithmetic Library)。

我想这应该是程序中比较之前 mpz_powm 运算的结果与程序中硬编码的值是否相等，如果相等则输出 tql。看到这里应该可以基本确定这是一道已知密文求解RSA明文的题目。

根据RSA的实现过程，首先来计算密钥。第一步是获得大整数 N ，根据程序可得

N = 10346103590081691412139010129904904441395040517371217043416168653987816098454

注意：这里的N是十进制表示的

然后对N进行大整数的因数分解，这里我用的是yafu工具

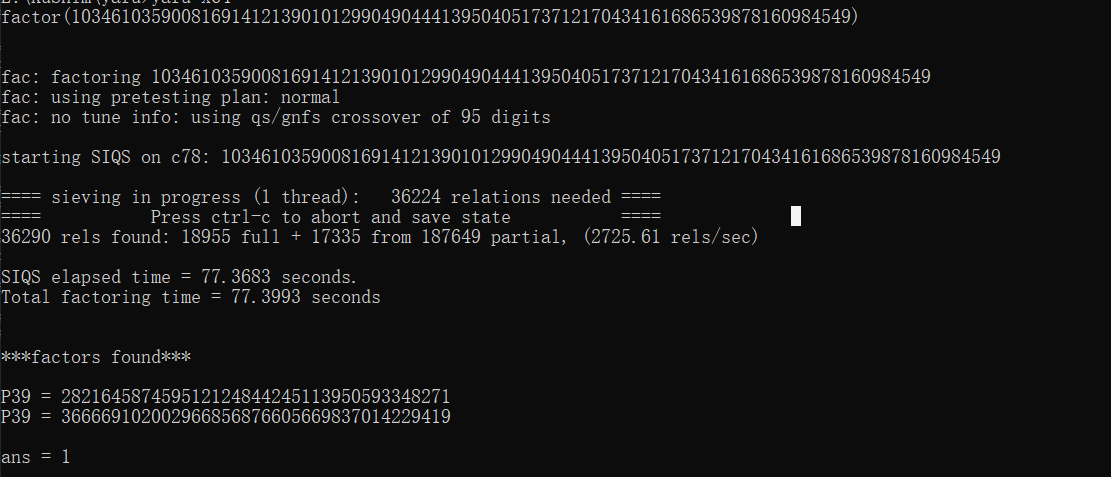
得到p和q

p = 366669102002966856876605669837014229419

q = 282164587459512124844245113950593348271

e = 65537(程序已给出)

接下来主要求出私钥d，并通过d得到明文m，在转换位ascll码即可

这是公式，图中的C是密文，M是明文，D是私钥（私钥由这个公式计算得出E * D % φ(N) = 1），N是公共模数（质数 P 、Q相乘得到N），MOD就是模运算

 

接下来就可以写脚本了

 

 

import gmpy2
import binascii

p = 282164587459512124844245113950593348271
q = 366669102002966856876605669837014229419
c = 0xad939ff59f6e70bcbfad406f2494993757eee98b91bc244184a377520d06fc35
n = 103461035900816914121390101299049044413950405173712170434161686539878160984549
e = 65537
d = gmpy2.invert(e,(p-1)*(q-1))
m = gmpy2.powmod(c,d,n)
print(binascii.unhexlify(hex(m)[2:]).decode(encoding="utf-8"))

 

注意：这里gmpy2模块是要下载安装的，可以自行在网上下载(我是下载的)

最后得出flag

suctf{Pwn_@_hundred_years}