PTZ2021sd3i Intellectual Implementation（扫描线技巧）
好消息：一发过了！是最优解！好高兴好高兴好高兴！
坏消息：最优解被 sb vjudge 抢了 QAQ！
题意：给你 \(n\) 个矩形，平行于坐标轴，求有多少个三元组 \((u, v, w),\ 1\leq u < v < w \leq n\)，满足这三个矩形无交。保证两个维度上所有值分别互不相同。
\(n\leq 2\cdot10^5\)
首先三个矩形无交实在是太难做了，变为总的减掉不合法，不合法的三元组有三种情况：两个之间有交而均与另一个无交、其中一个与另外两个有交而另外两个之间无交、三个之间互相有交。
分别记为 \(c_1,\ c_2,\ c_3\)，记有 \(d_i\) 个矩形和矩形 \(i\) 有交，手玩容易得到 \(\sum d_i(n - 2) = 2c_1 + 4c_2 + 6c_3\)（即尝试计数 \(c_1\) 得到的实际答案），\(\sum\binom{d_i}{2} = c_2 + 3c_3\)（即尝试计数 \(c_2\) 得到的实际答案），两式相减得到 \(c_1 + c_2\)，还差 \(c_3\)。
先考虑如何计数 \(d_i\)，考虑扫描线，从下往上扫，加入一个矩形的下边缘的时候数有几个和它有交，这可以用两颗树状树组实现，但是这样会算漏：
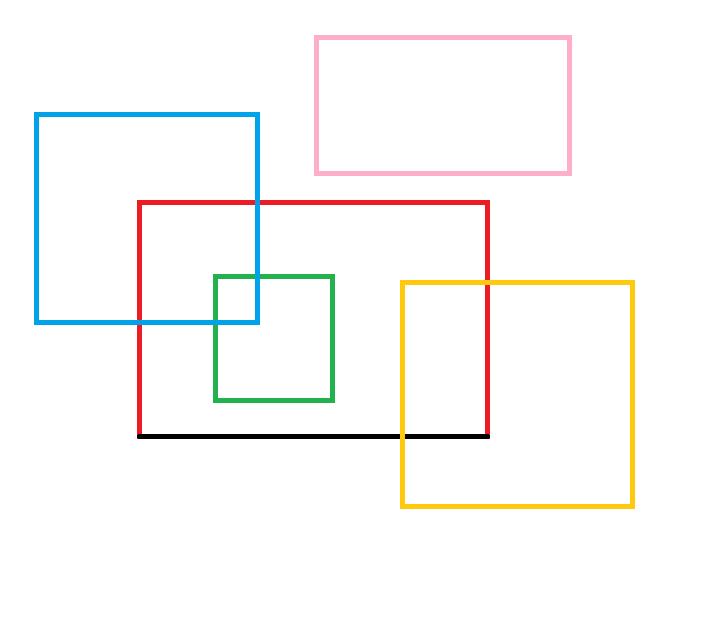
我们实际上只计数了黄色的矩形，然而我们可以利用类似差分的思想，再做一次扫描线，但这一次遇到上边缘不再删掉该矩形，而是保留，计算答案时用与上边缘有交的区间个数减去与下边缘有交的区间个数，然后两次扫描线答案加起来就是答案，具体看图，如果相离会在上下边缘各算一次所以没有贡献（记得去掉自己）。
然后就能得到 \(d_i\)。
接下来是 \(c_3\)，为了防止算重，我们需要考虑对于下边缘最高的矩形计数，还是上面的图，对于红绿蓝三个矩形，我们把贡献推到蓝色矩形上，扫描线时，相当于要求 \([l_u, r_u]\) 与 \([l_v, r_v],\ [l_w, r_w]\) 两两有交，这不好算，我们算 \([l_u, r_u]\) 与 \([l_v, r_v],\ [l_w, r_w]\) 分别有交减掉 \([l_v, r_v],\ [l_w, r_w]\) 无交的情况。总的情况仍然两个树状树组就行，无交相当于区间左边选一个右端点，右边选一个左端点，合并是容易的，直接上线段树就行。
最后答案就是 \(\binom{n}{3} - c_1 - c_2 - c_3\)。
code:
\(\texttt{C++17}\ \texttt{Ofast}\ \texttt{488ms}\ \texttt{6.2kb}\)
// No mind to think.
//
// No will to break.
//
// No voice to cry suffering.
//
// Born of God and Void.
//
// You shall seal the blinding light that plagues their dreams.
//
// You are the Vessel.
//
// You are the Hollow Knight.
#ifdef N2
#define _GLIBCXX_DEBUG
#define LOG(...) fprintf(stderr, __VA_ARGS__)
#define DO(...) __VA_ARGS__
#define NDO(...)
#else
#define LOG(...)
#define DO(...)
#define NDO(...) __VA_ARGS__
#endif
#define syncoff ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
// #pragma GCC target("avx")
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("no-stack-protector")
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int maxn = 2e5 + 10;
class Rect {
public:
int xl, yl, xr, yr;
Rect() = default;
Rect(int xl, int yl, int xr, int yr) : xl(xl), yl(yl), xr(xr), yr(yr) {}
};
class Seg {
public:
int l, r;
ll h;
Seg() = default;
Seg(int l, int r, ll h) : l(l), r(r), h(h) {}
};
vector<Rect> p;
vector<pair<Seg, int>> opt;
int n;
namespace Init {
vector<int> numx, numy;
void Init() {
for(auto r : p) numx.emplace_back(r.xl), numx.emplace_back(r.xr);
for(auto r : p) numy.emplace_back(r.yl), numy.emplace_back(r.yr);
sort(numx.begin(), numx.end());
sort(numy.begin(), numy.end());
for(auto &r : p) {
r = Rect(upper_bound(numx.begin(), numx.end(), r.xl) - numx.begin(),
upper_bound(numy.begin(), numy.end(), r.yl) - numy.begin(),
upper_bound(numx.begin(), numx.end(), r.xr) - numx.begin(),
upper_bound(numy.begin(), numy.end(), r.yr) - numy.begin());
}
for(int i = 0; i < p.size(); i++) {
opt.emplace_back(Seg(p[i].xl, p[i].xr, p[i].yl), i);
opt.emplace_back(Seg(p[i].xl, p[i].xr, p[i].yr), -i - 1);//!!!
}
sort(opt.begin(), opt.end(), [](pair<Seg, int> a, pair<Seg, int> b) {
return a.first.h < b.first.h;
});
}
}
class Fenwick {
public:
int tr[maxn << 1];
void clear() {memset(tr, 0, sizeof(tr));}
int __lowbit(int x) {return x & (-x);}
void modify(int x, int val, int n) {
while(x <= n) {
tr[x] += val;
x += __lowbit(x);
}
}
int __query(int x) {
int res = 0;
while(x) {
res += tr[x];
x -= __lowbit(x);
}
return res;
}
int query(int l, int r) {
if(l > r) return 0;
return __query(r) - __query(l - 1);
}
} R, L;
int Cap(int l, int r) {
return R.query(l, n << 1) - L.query(r + 1, n << 1);
}
class SegTree {
public:
Seg __merge(Seg a, Seg b) {return Seg(a.l + b.l, a.r + b.r, a.h + b.h + (ll)a.r * b.l);}
Seg tr[maxn << 3];
void __update(int k) {tr[k] = __merge(tr[k << 1], tr[k << 1 | 1]);}
void modify_l(int k, int l, int r, int addr, int val) {
if(l == r) {
tr[k].l += val;
return;
}
int mid = (l + r) >> 1;
if(addr <= mid) modify_l(k << 1, l, mid, addr, val);
else modify_l(k << 1 | 1, mid + 1, r, addr, val);
__update(k);
}
void modify_r(int k, int l, int r, int addr, int val) {
if(l == r) {
tr[k].r += val;
return;
}
int mid = (l + r) >> 1;
if(addr <= mid) modify_r(k << 1, l, mid, addr, val);
else modify_r(k << 1 | 1, mid + 1, r, addr, val);
__update(k);
}
Seg __query(int k, int l, int r, int L, int R) {
if(L <= l && r <= R) return tr[k];
int mid = (l + r) >> 1;
Seg res(0, 0, 0);
if(L <= mid) res = __merge(res, __query(k << 1, l, mid, L, R));
if(R > mid) res = __merge(res, __query(k << 1 | 1, mid + 1, r, L, R));
return res;
}
int query(int k, int l, int r, int L, int R) {return __query(k, l, r, L, R).h;}
}sgt;
namespace RectIntersect {
inline vector<int> Calc() {
vector<int> d(n);
for(auto cur : opt) {
int l = cur.first.l, r = cur.first.r, ord = cur.second;
if(ord < 0) {
int x = -ord - 1;
R.modify(r, -1, n << 1);
L.modify(l, -1, n << 1);
} else {
d[ord] += Cap(l, r);
R.modify(r, 1, n << 1);
L.modify(l, 1, n << 1);
}
}
R.clear(), L.clear();
for(auto cur : opt) {
int l = cur.first.l, r = cur.first.r, ord = cur.second;
if(ord < 0) {
int x = -ord - 1;
d[x] += Cap(l, r) - 1;
} else {
d[ord] -= Cap(l, r);
R.modify(r, 1, n << 1);
L.modify(l, 1, n << 1);
}
}
return d;
}
}
namespace TreeRectIntersect {
ll Calc() {
R.clear(), L.clear();
ll res = 0;
for(auto cur : opt) {
int l = cur.first.l, r = cur.first.r, ord = cur.second;
if(ord < 0) {
int x = -ord - 1;
R.modify(r, -1, n << 1);
L.modify(l, -1, n << 1);
sgt.modify_l(1, 1, n << 1, l, -1);
sgt.modify_r(1, 1, n << 1, r, -1);
} else {
int x = Cap(l, r);
res += (ll)x * (x - 1) / 2 - sgt.query(1, 1, n << 1, l, r);
R.modify(r, 1, n << 1);
L.modify(l, 1, n << 1);
sgt.modify_l(1, 1, n << 1, l, 1);
sgt.modify_r(1, 1, n << 1, r, 1);
}
}
return res;
}
}
int main() {
syncoff;
cin >> n;
for(int i = 1; i <= n; i++) {
int xl, xr, yl, yr;
cin >> xl >> xr >> yl >> yr;
p.emplace_back(xl, yl, xr, yr);
}
Init::Init();
vector<int> d = RectIntersect::Calc();
ll ans = 0, x1 = 0, x2 = 0, c3 = TreeRectIntersect::Calc();
for(int cur : d) {
x1 += (ll)cur * (n - 2);
x2 += (ll)cur * (cur - 1) / 2;
}
ans = (x1 / 2 - x2);
cout << (ll)n * (n - 1) * (n - 2) / 6 - ans - c3;
}
