二分图(例题)
https://www.cnblogs.com/kuangbiaopilihu/p/18184536
$\quad $ 这里不再介绍二分图的基础知识,只是一些例题的解释。
关押罪犯

$\quad $ 当然,这道题可以用二分+并查集来解决。但这是二分图专辑,所以介绍一下二分图做法。
$\quad $ 首先如果两个罪犯之间有仇恨,那么当他们不在同一所监狱时不会发生冲突。若要若干个罪犯之间不产生冲突,那么将有仇恨的罪犯连边,则不会发生冲突的罪犯恰好形成一个二分图。
$\quad $ 所以按照有仇恨罪犯之间的怒气值排序,再二分一下答案下标,把边权大于二分答案的边加进去,如果形成了一个二分图,则答案合法。然后便可得出答案。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+100;
vector<int> sl[N];
struct stu{
int x,y,w;
}s[N];
int col[N],n,m,ans;
bool is_gragh(int cur,int fa,int color){
col[cur]=color;
for(int i=0;i<sl[cur].size();i++){
int y=sl[cur][i];
if(col[y]==color)return false;
if(col[y]==0&&!is_gragh(y,cur,3-color))return false;
}
return true;
}
bool check(int x){
for(int i=1;i<=n;i++)sl[i].clear();
memset(col,0,sizeof col);
for(int i=x+1;i<=m;i++){
int x=s[i].x,y=s[i].y;
sl[x].push_back(y);
sl[y].push_back(x);
}
for(int i=1;i<=n;i++)if(col[i]==0)if(!is_gragh(i,0,1))return false;
return true;
}
bool cmp(stu a,stu b){return a.w<b.w;}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)scanf("%d%d%d",&s[i].x,&s[i].y,&s[i].w);
sort(s+1,s+1+m,cmp);
int l=0,r=m;
while(l<=r){
int mid=(l+r)>>1;
if(check(mid))r=mid-1,ans=mid;
else l=mid+1;
}
printf("%d",s[ans].w);
return 0;
}
\(\quad\)
Asteroids 穿越小行星群
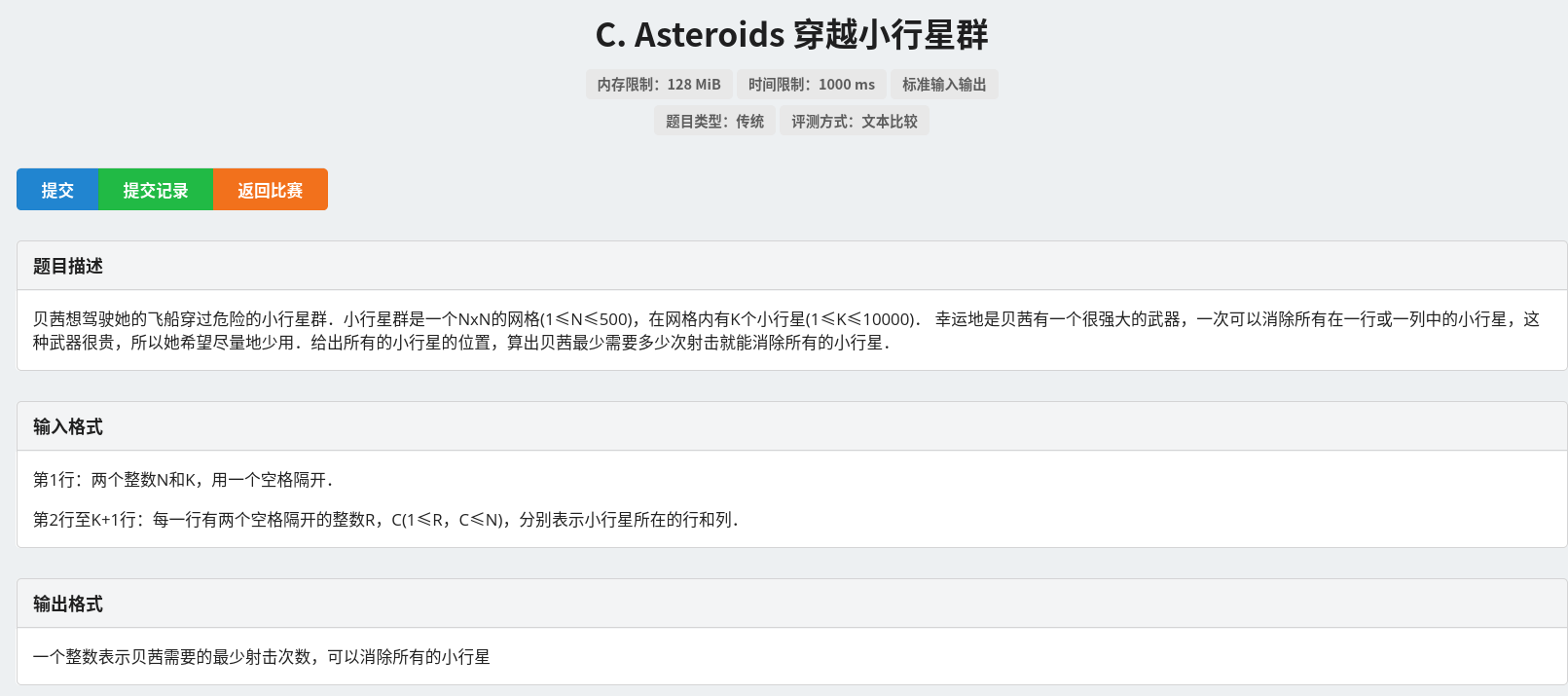
$\quad $ 可以发现,如果选择了一列,那么处于这一列的点将都被消除,那么就可以将该点与其所在行与所在列相连,以表示其关联。先拿样例举例:
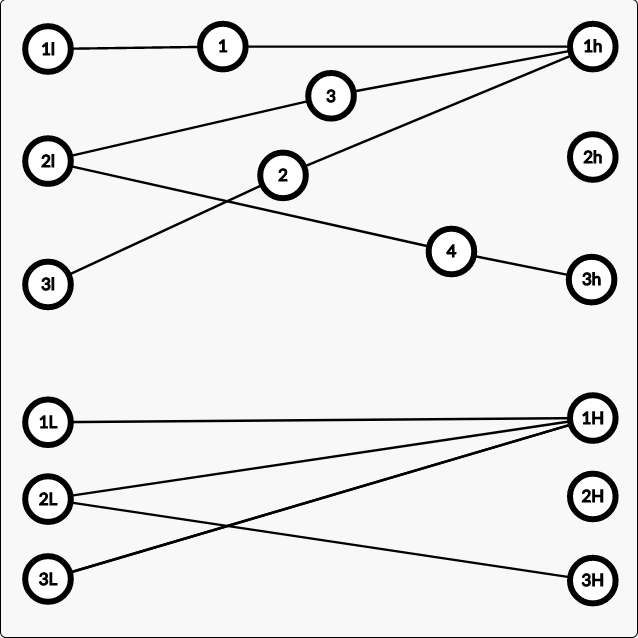
$\quad $ 我们发现,点只存在于行和列之间的边上,那么将点省去,可以得到一个二分图。这样问题就变为了一个二分图的点最大覆盖问题,求最大匹配即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+100;
bool vis[N];
int n,k,match[N];
vector<int> s[N<<1];
bool dfs(int x){
for(int i=0;i<s[x].size();i++){
int y=s[x][i];
if(!vis[y]){
vis[y]=1;
if(!match[y]||dfs(match[y])){
match[y]=x;
return true;
}
}
}
return false;
}
int Hungary(){
int ans=0;
for(int i=1;i<=n;i++){
memset(vis,0,sizeof vis);
if(dfs(i))ans++;
}
return ans;
}
int main(){
scanf("%d%d",&n,&k);
n<<=1;
for(int i=1;i<=k;i++){
int x,y;
scanf("%d%d",&x,&y);
y+=n;
s[x].push_back(y);
s[y].push_back(x);
}
printf("%d",Hungary());
return 0;
}
\(\quad\)
超级英雄Hero
$\quad $ 还是先膜样例,这里用汉字表示锦囊,阿拉伯数字表示题目。
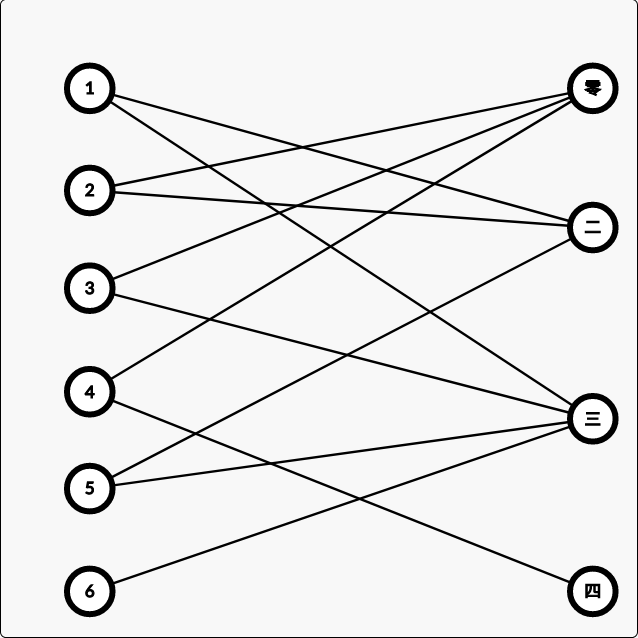
$\quad $ 同样可以得到一张二分图,只不过这道题不是要求最大匹配,因为答题出现错误就淘汰了,仔细观察匈牙利算法代码,可以发现他正是从1顺序开始寻找的,所以我们只要在无法匹配时打断循环即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+100;
bool vis[N];
int n,k,match[N];
vector<int> s[N<<1];
bool dfs(int x){
for(int i=0;i<s[x].size();i++){
int y=s[x][i];
if(!vis[y]){
vis[y]=1;
if(!match[y]||dfs(match[y])){
match[y]=x;
return true;
}
}
}
return false;
}
int Hungary(){
int ans=0;
for(int i=1;i<=n;i++){
memset(vis,0,sizeof vis);
if(dfs(i))ans++;
else break;
}
return ans;
}
int main(){
scanf("%d%d",&n,&k);
for(int i=1;i<=k;i++){
int x,y;
scanf("%d%d",&x,&y);
x++,y++;
s[i].push_back(y);
s[i].push_back(x);
}
printf("%d",Hungary());
return 0;
}
\(\quad\)
Way Selection
$\quad $ 先求出所有小衫到所有出口所需时间,对时间小于k的情况,就将两者相连,最后还是的到一张二分图,此时只需要求出最大匹配即可。
注意开double!!
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+100;
bool vis[N];
int n,k,match[N],m;
vector<int> s[N<<1];
double x[N],y[N];
bool dfs(int x){
for(int i=0;i<s[x].size();i++){
int y=s[x][i];
if(!vis[y]){
vis[y]=1;
if(!match[y]||dfs(match[y])){
match[y]=x;
return true;
}
}
}
return false;
}
int Hungary(){
int ans=0;
for(int i=1;i<=m;i++){
memset(vis,0,sizeof vis);
if(dfs(i))ans++;
}
return ans;
}
int main(){
scanf("%d%d%d",&m,&n,&k);
//m是小衫个数,n是点数,k是边权最大值。
for(int i=1;i<=n;i++)scanf("%lf%lf",&x[i],&y[i]);
for(int i=1;i<=m;i++){
double xl,yl,vl,tl;
scanf("%lf%lf%lf",&xl,&yl,&vl);
for(int j=1;j<=n;j++){
tl=sqrt((x[j]-xl)*(x[j]-xl)+(y[j]-yl)*(y[j]-yl));
tl/=vl;
// cout<<tl<<endl;
if(k>=tl)s[i].push_back(j+m),s[j+m].push_back(i);
}
}
printf("%d",Hungary());
return 0;
}
\(\quad\)
放置机器人
$\quad $ 这道题和穿越小行星群很像,但是有石头阻拦,对于有石头阻拦的,我们可以将一行视为两行、一列视为两列,再将合法的位置与其行列连边。这样又得到一张二分图,再求最大匹配即可。
点击查看代码
#inclu de<bits/stdc++.h>
using namespace std;
const int N=65;
char ch[N*N][N*N];
bool vis[N*N];
int n,m,match[N*N],row[N*N][N*N],col[N*N][N*N];
int ntot,ltot;
vector<int>s[N*N];
bool dfs(int x){
for(int i=0;i<s[x].size();i++){
int y=s[x][i];
if(!vis[y]){
vis[y]=1;
if(!match[y]||dfs(match[y])){
match[y]=x;
return true;
}
}
}
return false;
}
int Hungary(){
int ans=0;
for(int i=1;i<=ntot;i++){
memset(vis,0,sizeof vis);
if(dfs(i))ans++;
}
return ans;
}
int main(){
scanf("%d%d",&m,&n);
for(int i=1;i<=m;i++)scanf("%s",ch[i]+1);
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
if(ch[i][j]-'#'){
if(j>1&&ch[i][j-1]-'#')row[i][j]=row[i][j-1];
else row[i][j]=++ntot;
if(i>1&&ch[i-1][j]-'#')col[i][j]=col[i-1][j];
else col[i][j]=++ltot;
}
}
}
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
if(ch[i][j]=='o')s[row[i][j]].push_back(col[i][j]+ntot);
}
}
printf("%d",Hungary());
}
\(\quad\)
Treasure Exploration
$\quad $ 这题涉及了一个传递闭包的问题,就是用Floyd来判断两个点是否联通(当然这道题里是单向联通),在加边后跑一边匈牙利找一下最大独立集(就是点数减去最小顶点覆盖),最终答案就是结果。
$\quad $ 但是匈牙利跑法与板子略有不同,只要两点可以联通,就认为是原先匈牙利中的直接相连。
多测记得清空
点击查看代码
#include<bits /stdc++.h>
using namespace std;
const int N=550;
bool vis[N],d[N][N];
int match[N],n,m;
bool dfs(int x){
for(int i=1;i<=n;i++){
if(!vis[i]&&d[x][i]){
vis[i]=1;
if(!match[i]||dfs(match[i])){
match[i]=x;
return true;
}
}
}
return false;
}
int Hungary(){
int ans=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++)vis[j]=0;
ans+=dfs(i);
}
return ans;
}
int main(){
while(scanf("%d%d",&n,&m)!=EOF&&(n||m)){
memset(match,0,sizeof match);
for(int i=1;i<=m;i++){
int x,y;
scanf("%d%d",&x,&y);
d[x][y]=1;
}
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(d[i][k]&&d[k][j])d[i][j]=1;
}
}
}
printf("%d\n",n-Hungary());
for(int i=1;i<=n;i++){
match[i]=0;
for(int j=1;j<=n;j++)d[i][j]=0;
}
}
return 0;
}
\(\quad\)
攻击装置

$\quad $ 这道题和前面的放置机器人还有猫和狗都是属于一类题,都是存在一个攻击范围,问能放置几个的问题,大致思路就是将有冲突的几个点连起来狗更一个二分图,再求其最大独立集即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=320050,M=205*205;
bool vis[M];
int to[N],nt[N],h[M],n,cnt,tot,match[M];
int qx[5]={0,-1,-1,-2,-2},qy[5]={0,2,-2,1,-1};
map<int,int>mp[205];
char ch[205][205];
void add(int x,int y){
to[++cnt]=y;
nt[cnt]=h[x];
h[x]=cnt;
}
bool dfs(int x){
for(int i=h[x];i;i=nt[i]){
int y=to[i];
if(!vis[y]){
vis[y]=1;
if(!match[y]||dfs(match[y])){
match[y]=x;
return true;
}
}
}
return false;
}
int Hungary(){
int ans=0;
for(int i=1;i<=tot;i++){
memset(vis,0,sizeof vis);
ans+=dfs(i);
}
return ans;
}
int main(){
freopen("attack.in","r",stdin);
freopen("attack.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%s",ch[i]+1);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(ch[i][j]=='0'){
mp[i][j]=++tot;//对于每个可放置的点编号
for(int k=1;k<=4;k++){//先处理现在所在点上方的点(因为已经编号了)
if(1<=(i+qx[k])&&(i+qx[k])<=n){
if(1<=j+qy[k]&&j+qy[k]<=n){
add(tot,mp[(i+qx[k])][j+qy[k]]);
add(mp[(i+qx[k])][j+qy[k]],tot);
}
}
}
}
}
}
printf("%d",tot-Hungary()/2);
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号