数据结构和算法总结（一）：广度优先搜索BFS和深度优先搜索DFS
前言
这几天复习图论算法，觉得BFS和DFS挺重要的，而且应用比较多，故记录一下。
广度优先搜索
有一个有向图如图a
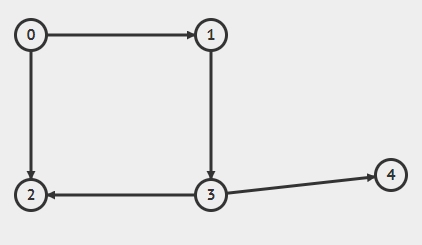
图a
广度优先搜索的策略是：
从起始点开始遍历其邻接的节点，由此向外不断扩散。
1.假设我们以顶点0为原点进行搜索，首先确定邻接0的顶点集合S0 = {1，2}。
2.然后确定顶点1的集合S1 = {3}，顶点2没有邻接点，所以集合为空。
3.然后确定3的邻接点集合S3，因为2已经被遍历过，所以不考虑，所以由顶点3知道的邻接点集合S3 = {4}。
4.然后再确定顶点4的邻接点集合,顶点4没有更多的邻接点了，此时也没有还未遍历的邻接点集合，搜索终止。
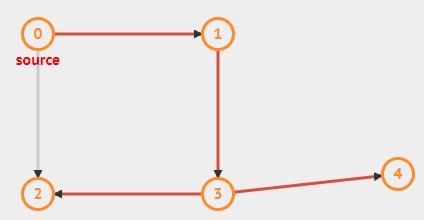
遍历的路径可以参考如下图红色标记的路径：
动态过程
代码的实现思路：
BFS()
{
输入起始点； 初始化所有顶点标记为未遍历； 初始化一个队列queue并将起始点放入队列； while（queue不为空） {
从队列中删除一个顶点s并标记为已遍历； 将s邻接的所有还没遍历的点加入队列； }
}
深度优先遍历
继续以图a为例
图a
深度优先遍历的策略是：
从一个顶点v出发，首先将v标记为已遍历的顶点，然后选择一个邻接于v的尚未遍历的顶点u，如果u不存在，本次搜素终止。如果u存在，那么从u又开始一次DFS。如此循环直到不存在这样的顶点。
比如图a中
1.从顶点0开始，将0标记为已遍历，然后选择未被遍历的邻接0的顶点1。
2.标记顶点1，然后选择3并标记，然后选择顶点3邻接的顶点2。
3.顶点2标记后没有与它邻接的未标记的点，所以返回3选择另一个邻接3并且未被标记的顶点4。
4.顶点4没有更多的符合条件的点，因此搜索终止，返回到3，3没有更多的点，搜索终止返回到1，最后返回到0，搜索终止。
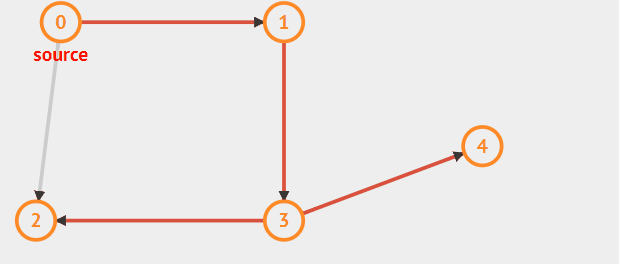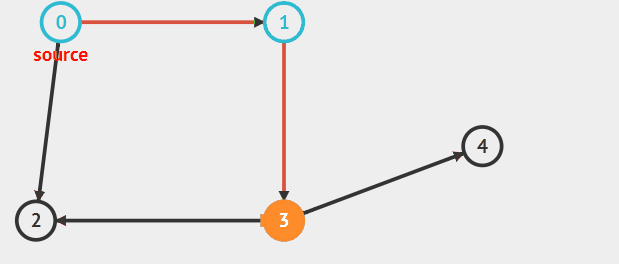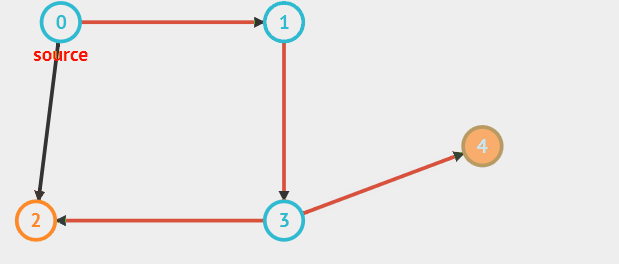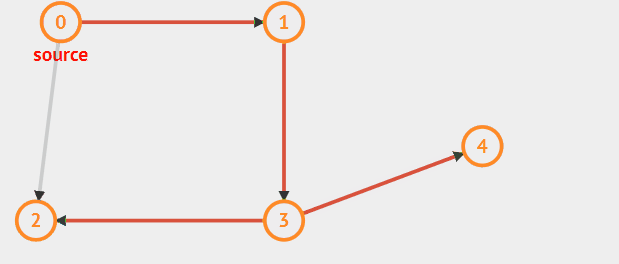
遍历的路径可以参考如下图红色标记的路径：
动态过程
代码的实现思路：
DFS（顶点v） { 标记v为已遍历； for（对于每一个邻接v且未标记遍历的点u） DFS（u）; }
一个简单的应用
问题不赘述，具体可参考 LeetCode朋友圈问题 。
实现的代码如下（C#）：
public class Solution { public void dfs(int [,]M,int []visit,int i) { for(int j = 0;j < M.GetLength(0);j++) { if(M[i,j] == 1 && visit[j] == 0) { visit[j] = 1; dfs(M,visit,j); } } } public void bfs(int [,]M,int []visit,int i) { Queue<int> q = new Queue<int>(); q.Enqueue(i); while(q.Count > 0) { int temp = q.Dequeue(); for(int j = 0;j < M.GetLength(0);j++) { if(M[temp,j] == 1 && visit[j] == 0) { visit[j] = 1; q.Enqueue(j); } } } } public int FindCircleNum(int[,] M) { int N = M.GetLength(0); int circle = 0; //朋友圈数 int[] visit = new int[N]; for(int i = 0;i < N;i++) { if(visit[i] == 0) //还没被遍历过 { //dfs(M,visit,i); //使用dfs搜索并标记与其相关的学生 bfs(M,visit,i); //使用bfs搜索并标记与其相关的学生 circle++; } } return circle; } }
参考资料
《数据结构、算法与应用——C++描述》 作者：【美】 萨特吉·萨尼 机械工业出版社
