数据结构和算法总结(三):A* 寻路算法
前言
复习下寻路相关的东西,而且A star寻路在游戏开发中应用挺多的,故记录下。
正文
迪杰斯特拉算法
说起A*得先谈谈Dijkstra算法,它是在BFS基础上的一种带权值的两点最短寻路贪心算法。
算法步骤
0.初始化图,输入起点,将所有点到起始点的距离设置为∞。
1.将起始点OriginNode记录为已访问,并从OriginNode开始将周围的点加入到待遍历列表中,更新到达这些点的距离,并将他们的父节点设置为起始点OriginNode。
2.如果待遍历列表不为空,则从列表中取出到达距离最小的点currentNode;反之则跳到第5步。
3.遍历currentNode邻接的点neighbors:
1) 如果已访问过,则遍历其他点。
2) 如果邻接的某点neighbor已经在待遍历列表中,则比较neighbor当前的距离distance(OriginNode,neighbor) 与 distance(OriginNode,currentNode) + distance(currentNode,neighbor), 如果后者更小,则将neighbor的距离值更新为该值并将父节点设置为currentNode。
3) 如果不在待遍历列表,则将neighbor放入待遍历列表,并则将neighbor的距离值更新为 distance(OriginNode,currentNode) + distance(currentNode,neighbor), 并将父节点设置为currentNode。
4.重复第2步
5.输入终点,从终点开始回溯父节点,打印路径。
动态过程

A* 寻路算法
A*的思路其实与Dijkstra一致,相比较Dijkstra,A*引入了一个启发公式来衡量消耗
其中 g(n) 代表从起始点到当前点的消耗,h(n) 代表终点到当前点的预估消耗(通常用曼哈顿距离或者欧拉距离衡量,这里不赘述,参考)。
算法思路
/*
A*寻路算法
带权值的BFS
每个点保存达到该点的消耗F = G值(出发点到当前点的代价值) + H值(目标点到当前点的预估距离,常用曼哈顿距离或者欧拉距离)
维护着两个列表,开放列表和关闭列表
逻辑:
初始化列表Close,Open,Path,将StartNode放入Open列表中
while(true)
{
从Open表中取得F值最小的节点CurrentNode.
从Open表中删除CurrentNode
将CurrentNode加入Close表中
if ( CurrentNode 是 目标点targetNode)
{
从CurrentNode点回溯直到起点并将所有回溯的节点加入Path表
打印Path表
return;
}
for (CurrentNode 的每一个邻接点 neighbor)
{
if(neighbor 在 Close表中 || neighbor 不可通行)
{
continue;
}
if(neighbor 在 Open表中)
{
if( CurrentNode 到达neighbor的消耗costG + node的G值 < neighbor的G值)
{
更新neighbor的G值;
将neighbor的回溯节点fatherNode设置为CurrentNode;
}
}
else
{
更新neighbor的G值;
更新neighbor的H值;
将neighbor的回溯节点fatherNode设置为CurrentNode;
将neighbor放入Open列表;
}
}
}
*/
动态过程
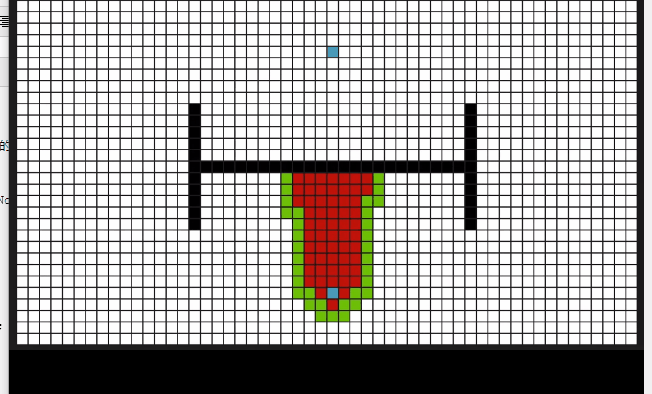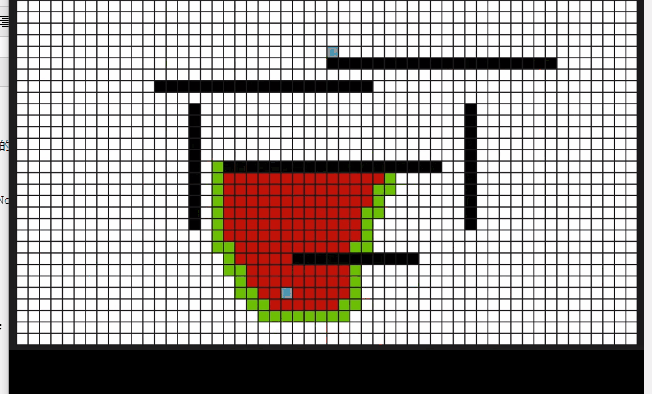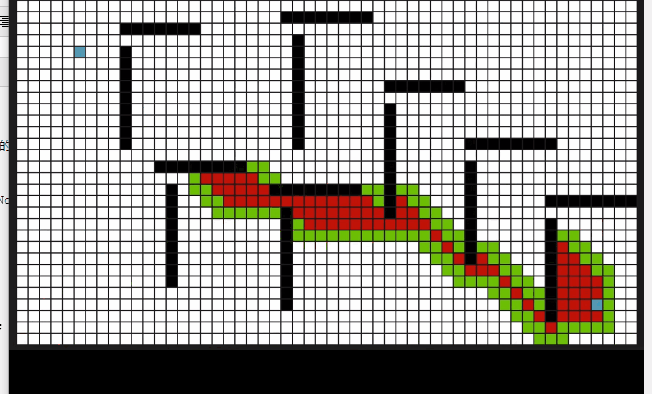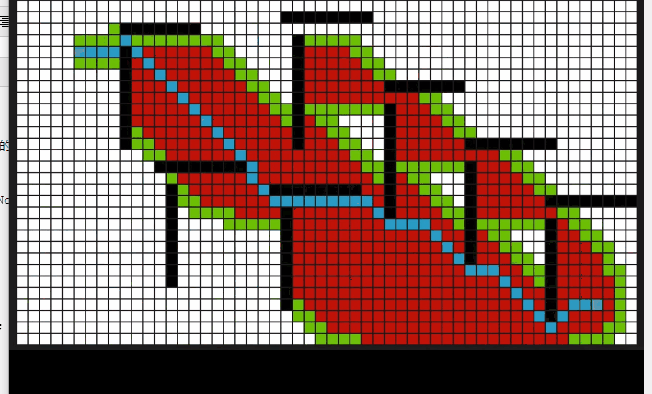
代码:
AstarNode的定义实现.
Astar.h
#pragma once
#include <vector>
#include <math.h>
using std::vector;
class AstarNode
{
private:
int m_igValue;
int m_ihValue;
int m_ifValue;
AstarNode* m_father;
public:
int x;
int y;
bool isPass;
public:
void SetG(int iValue);
int GetG() const;
int GetH() const;
int GetF() const;
void CalculateH(const AstarNode* endNode);
void SetFather(AstarNode* node);
AstarNode* GetFather() const;
bool isInList(const vector<AstarNode*>& nodeList) const;
public:
AstarNode();
AstarNode(int x,int y);
AstarNode(const AstarNode& node);
~AstarNode();
AstarNode& operator=(const AstarNode& node);
};
Astar.cpp
#include "Astar.h"
AstarNode::AstarNode()
{
isPass = true;
m_igValue = 0;
m_ihValue = 0;
m_ifValue = 0;
m_father = nullptr;
}
AstarNode::AstarNode(int x,int y)
{
isPass = true;
m_igValue = 0;
m_ihValue = 0;
m_ifValue = 0;
m_father = nullptr;
this->x = x;
this->y = y;
}
AstarNode::AstarNode(const AstarNode& node)
{
isPass = node.isPass;
m_igValue = node.GetG();
m_ihValue = node.GetH();
m_ifValue = node.GetF();
m_father = node.GetFather();
this->x = node.x;
this->y = node.y;
}
AstarNode& AstarNode::operator=(const AstarNode& node)
{
isPass = node.isPass;
m_igValue = node.GetG();
m_ihValue = node.GetH();
m_ifValue = node.GetF();
m_father = node.GetFather();
this->x = node.x;
this->y = node.y;
return *this;
}
AstarNode::~AstarNode()
{
}
void AstarNode::SetG(int iValue)
{
m_igValue = iValue;
}
int AstarNode::GetG() const
{
return m_igValue;
}
int AstarNode::GetF() const
{
return m_igValue + m_ihValue;
}
int AstarNode::GetH() const
{
return m_ihValue;
}
void AstarNode::CalculateH(const AstarNode* endNode)
{
m_ihValue = abs(endNode->x - x) + abs(endNode->y - y);
}
void AstarNode::SetFather(AstarNode* node)
{
m_father = node;
}
AstarNode* AstarNode::GetFather() const
{
return m_father;
}
bool AstarNode::isInList(const vector<AstarNode*>& nodeList) const
{
for(auto iter = nodeList.begin();iter != nodeList.end();iter++)
{
if((*iter)->x == this->x && (*iter)->y == this->y)
return true;
}
return false;
}
main.cpp
#include "Astar.cpp"
#include <algorithm>
using namespace std;
/*
'e' 终点
's' 起点
'#' 障碍物
'-' 可通行点
'o' 回溯路径节点
*/
vector<vector<char>> graph = {
{'-', '-', '-', '-', '-', '-', '-'},
{'-', '-', 'e', '#', '-', '-', '-'},
{'-', '#', '#', '#', '#', '-', '-'},
{'-', '-', '-', '-', '#', '#', '-'},
{'-', '-', '#', '-', '#', '-', '-'},
{'-', '-', '-', '#', '-', '-', '-'},
{'-', '-', '-', '-', '-', '-', 's'},
};
void BuildGraph(vector<vector<AstarNode *>> &astarGraph, AstarNode &start, AstarNode &end)
{
for (int i = 0; i < astarGraph.size(); i++)
{
auto row = astarGraph[i];
for (int j = 0; j < row.size(); j++)
{
char mark = graph[i][j];
if (mark == 's')
{
start.x = i;
start.y = j;
start.SetG(0);
start.CalculateH(&end);
astarGraph[i][j] = &start;
}
else if (mark == 'e')
{
end.x = i;
end.y = j;
astarGraph[i][j] = &end;
}
else if (mark == '#')
{
astarGraph[i][j] = new AstarNode(i, j);
astarGraph[i][j]->isPass = false;
}
else
{
astarGraph[i][j] = new AstarNode(i, j);
}
}
}
}
void printGraph()
{
for (int i = 0; i < graph.size(); i++)
{
auto line = graph[i];
for (int j = 0; j < line.size(); j++)
{
cout << line[j] << " ";
}
cout << endl;
}
}
vector<AstarNode *>::iterator GetMinFNode(vector<AstarNode *> &openList)
{
auto tmp = openList.begin();
for (auto iter = openList.begin(); iter != openList.end(); iter++)
{
if ((*iter)->GetF() < (*tmp)->GetF())
{
tmp = iter;
}
}
return tmp;
}
inline int GetCost(int xDiff, int yDiff)
{
if (xDiff == 0 || yDiff == 0)
return 10;
return 14;
}
void SearchOneNode(AstarNode ¤tNode, AstarNode &neighbor, AstarNode &startNode, AstarNode &endNode, vector<AstarNode *> &openList, vector<AstarNode *> &closeList)
{
if (neighbor.isInList(closeList) || !neighbor.isPass)
return;
int gCost = GetCost(currentNode.x - neighbor.x, currentNode.y - neighbor.y);
if (neighbor.isInList(openList))
{
if (currentNode.GetG() + gCost < neighbor.GetG())
{
neighbor.SetG(currentNode.GetG() + gCost);
neighbor.SetFather(¤tNode);
}
}
else
{
neighbor.SetG(currentNode.GetG() + gCost);
neighbor.SetFather(¤tNode);
neighbor.CalculateH(&endNode);
openList.push_back(&neighbor);
}
}
void Astar()
{
vector<AstarNode *> OpenList;
vector<AstarNode *> CloseList;
vector<AstarNode *> Path;
size_t len = graph.size();
vector<vector<AstarNode *>> astarGraph(len, vector<AstarNode *>(len));
AstarNode startNode;
AstarNode endNode;
BuildGraph(astarGraph, startNode, endNode);
OpenList.push_back(&startNode);
while (!OpenList.empty())
{
auto it = GetMinFNode(OpenList);
AstarNode *currentNode = *it;
OpenList.erase(it);
CloseList.push_back(currentNode);
if (currentNode->x == endNode.x && currentNode->y == endNode.y)
{
while (currentNode->GetFather())
{
graph[currentNode->x][currentNode->y] = graph[currentNode->x][currentNode->y] == '-' ? 'o' : 'e';
Path.push_back(currentNode);
currentNode = currentNode->GetFather();
}
printGraph();
break;
}
int curX = currentNode->x;
int curY = currentNode->y;
int row = graph.size();
int column = row;
if (curX + 1 < row)
SearchOneNode(*currentNode, *astarGraph[curX + 1][curY], startNode, endNode, OpenList, CloseList);
if (curX - 1 >= 0)
SearchOneNode(*currentNode, *astarGraph[curX - 1][curY], startNode, endNode, OpenList, CloseList);
if (curY + 1 < column)
SearchOneNode(*currentNode, *astarGraph[curX][curY + 1], startNode, endNode, OpenList, CloseList);
if (curY - 1 >= 0)
SearchOneNode(*currentNode, *astarGraph[curX][curY - 1], startNode, endNode, OpenList, CloseList);
if (curX - 1 >= 0 && curY - 1 >= 0)
SearchOneNode(*currentNode, *astarGraph[curX - 1][curY - 1], startNode, endNode, OpenList, CloseList);
if (curX - 1 >= 0 && curY + 1 < column)
SearchOneNode(*currentNode, *astarGraph[curX - 1][curY + 1], startNode, endNode, OpenList, CloseList);
if (curX + 1 < row && curY - 1 >= 0)
SearchOneNode(*currentNode, *astarGraph[curX + 1][curY - 1], startNode, endNode, OpenList, CloseList);
if (curX + 1 < row && curY + 1 < row)
SearchOneNode(*currentNode, *astarGraph[curX + 1][curY + 1], startNode, endNode, OpenList, CloseList);
}
cout << endl;
}
int main()
{
auto start = chrono::steady_clock::now();
Astar();
auto end = chrono::steady_clock::now();
cout << chrono::duration<double, milli>(end - start).count() << " ms" << endl;
getchar();
}
参考资料



