ARC143
ARC143
考试情况:一眼订正,鉴定为做出前三题。
A - Three Integers
以前做过 \(n\) 个数的版本,当时还被某人嘲讽说“堆,贪心,这都做不出来?”。
\(3\) 个数就考虑最大数怎么消掉。
如果最大数比其它两个数之和还大,就无解。
否则每次都让最大值减一,使得操作次数为最大值的大小是最优情况。
可以构造很多不同的方案使得最少操作数量为最大值,我的方法是先选择最大值和最小值,将最大值减到中间值的大小,显然最小值够减。然后再将 \(3\) 个数一起减直到最小值为 \(0\),然后将剩下两个相同大小的值一起减到 \(0\)。
代码:
点击查看代码
#include <bits/stdc++.h>
using namespace std;
long long A,B,C;
long long Sum,Max,Min;
int main()
{
cin>>A>>B>>C;
Sum=A+B+C;
Max=max(max(A,B),C);
if(Max>Sum-Max)
{
puts("-1");
return 0;
}
cout<<Max;
}
B - Counting Grids
题意是说将 \(1\) 到 \(N^2\) 填入一个 \(N \times N\) 的矩阵,要求每个数都满足同一列中存在一个数比自己大或同一行中存在一个数比自己小,求方案数。
正难则反,考虑不合法情况。对于一个数字 \(x\),无论它在哪个格子,想让它不合法,就得让它这一列的所有值比 \(x\) 小,它这一行的所有值比 \(x\) 大。
然后对于跟 \(x\) 不在同一行也不在同一列的数字 \(y\),
-
\(y>x\)
\(y\) 一定大于 \(x\) 所在列 \(y\) 所在行的那一个格子,因为那一个格子比 \(x\) 小。
-
\(y<x\)
\(y\) 一定小于 \(x\) 所在行 \(y\) 所在列的那一个格子,因为那一个格子比 \(x\) 大。
所以对于任意合法方案,最多只有一个格子不合法。于是只需要枚举不合法的格子的值,然后算方案,答案为 \((N^2)!\) 减去不合法方案数。
对于一个值为 \(x\) 的格子,它所在列的取值范围为 \([1,x-1]\),放置方案数为这里面的数选 \(N-1\) 个的排列数。所在行取值范围为 \([N^2-x+1,N^2]\) ,同理。然后其它 \(N^2-(N-1)-(N-1)+1\) 个值任意放,方案数为其阶乘。把以上三个值乘起来就是当不合法格子为 \(x\) 的方案数。
代码:
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int MAXN=1e6+50,P=998244353;
long long Pow(long long a,long long b)
{
long long ans=1;
while(b)
{
if(b&1)
{
ans=ans*a%P;
}
a=a*a%P;
b>>=1;
}
return ans;
}
long long jc[MAXN];
long long A(long long n,long long m)
{
if(n<m)
return 0;
return jc[n]*Pow(jc[n-m],P-2)%P;
}
long long N;
long long ans;
int main()
{
cin>>N;
jc[0]=1;
for(int i=1;i<=N*N;i++)
jc[i]=jc[i-1]*i%P;
for(int i=1;i<=N*N;i++)
{
ans=(ans+N*N*A(i-1,N-1)%P*A(N*N-i,N-1)%P*jc[N*N-N-N+1]%P)%P;
}
cout<<(jc[N*N]-ans+P)%P;
}
C - Piles of Pebbles
我没看过官方题解,就说我考试的时候的做法。
把 Takahashi 叫做 \(X\),他能取得石头数也叫做 \(X\)。
Aoki 同理。
凭借直觉,最后答案只与 \(A_i \bmod (X+Y)\) 有关。感性理解就是,只要一个地方可以支持 \(X\) 取一次 \(Y\) 再取一次,那么取的这两次就没有意义,对可取性不造成影响。
然后分类讨论:
-
\(X \geq Y\)
此时 \(Y\) 的能取点大于等于 \(X\) 的能取点。\(Y\) 的策略一定是每次 \(X\) 取了之后,\(Y\) 取 \(X\) 本来能取的点,最后一定是两种情况之一:
- \(Y\) 取了最后一个 \(X\) 能取的点,\(X\) 没得取了。
- \(X\) 取了最后一个它能取的点。
显然 \(X\) 跟 \(Y\) 这样耗是可能会输的,于是 \(X\) 一定会选择一次把所有他能取的所有点全都取完,只要存在一个点 \(Y\) 能取而 \(X\) 不能取,\(Y\) 就赢了,否则 \(X\) 就赢了。
-
\(X < Y\)
\(Y\) 一定跟 \(X\) 的想法是一样的,而 \(X\) 在能取双方都能取的石头时一定不会取只有自己能取的石头,所以近似看成跟上一种情况,只是结果刚好相反罢了。
代码:
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int MAXN=1e6+50;
int N,X,Y;
int A[MAXN];
int main()
{
cin>>N>>X>>Y;
for(int i=1;i<=N;i++)
{
cin>>A[i];
A[i]=(A[i]%(X+Y));
}
bool flag=false;
if(X>=Y)
{
for(int i=1;i<=N;i++)
if(A[i]<X&&A[i]>=Y)
flag=true;
if(flag)
puts("Second");
else
puts("First");
return 0;
}
for(int i=1;i<=N;i++)
if(A[i]<Y&&A[i]>=X)
flag=true;
if(flag)
puts("First");
else
puts("Second");
return 0;
}
D - Bridges
貌似官方题解还没出。(下午出了)
题目可以理解为一共 \(N\) 个点,把点 \(i\) 拆成 \(2\) 个点,对应点相连。然后给 \(M\) 条边,可以选择 \(A_i\) 连 \(B'_i\),也可以选择 \(A'_i\) 连 \(B_i\),怎样连接才能使图中的桥最少。桥就是边双联通分量里的桥。
可以把这题看做是给一个 \(M\) 条边的无向图,要给这个图定向使得处于强联通分量里的点最多。
不就是造环嘛,跑 dfs,对于树边就向下定向,对于返祖边就向上定向,能成环的重定向之后还是环。环就是强联通分量。
值得注意的是,边可能会重复遇到,其定向以第一次定向为准。若此边已经被定向则不再重定向。
代码:
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int MAXN=1e6+50;
int N,M;
int A[MAXN],B[MAXN];
struct Edge
{
int x,y,Next;
}e[MAXN<<1];
int elast[MAXN],tot=1;
void Add(int x,int y)
{
tot++;
e[tot].x=x;
e[tot].y=y;
e[tot].Next=elast[x];
elast[x]=tot;
}
int ans[MAXN];
bool vis[MAXN];
bool vis2[MAXN];
void dfs(int u)
{
vis2[u]=true;
for(int i=elast[u];i;i=e[i].Next)
{
int v=e[i].y;
if(vis2[v])
{
if(vis[i]==false)
{
vis[i]=vis[i^1]=true;
ans[i]=i&1;
}
}
else
{
ans[i]=i&1;
vis[i]=vis[i^1]=1;
dfs(v);
}
}
}
int main()
{
scanf("%d%d",&N,&M);
for(int i=1;i<=M;i++)
{
scanf("%d",&A[i]);
}
for(int i=1;i<=M;i++)
{
scanf("%d",&B[i]);
Add(A[i],B[i]);
Add(B[i],A[i]);
}
for(int i=1;i<=N;i++)
{
if(vis2[i]==false)
dfs(i);
}
for(int i=1;i<=M;i++)
{
printf("%d",max(ans[i*2],ans[i*2+1]));
}
}
E - Reversi
官方题解还没出。(下午出了)
其实是一个复合型问题。
设 \(Can_i\) 表示在消除完 \(i\) 的子树的所有点只剩下 \(i\) 时,\(i\) 是不是白色的。
考虑叶子,颜色已经确定了,白色的一定不能变颜色,黑色一定必须变颜色。
考虑儿子全为叶子的点,操作顺序一定是先删除所有白色的,然后如果此节点为黑色,则需要上面支援变为白色,如果此节点为白色,这删除这个节点,将所有黑儿子变白,再将那些变白的儿子删掉。会发现如果没有支援,这个节点的颜色还是确定的。然后它的儿子节点没有变数,可以看做没有。
所以第一部分,可以通过 DP 算出每个点如果没有支援的颜色,然后再考虑这个“强制性支援”。如果儿子是白色的,那一定要支援父亲,如果儿子是黑色的,一定要父亲支援。所以这是一个有向图,每条边代表一个支援关系(必须支援)。
然后拿堆贪心地跑拓扑排序就好了。
如何判无解?拓扑排序的过程中模拟原树的颜色变化(删点改变周围的颜色),如果发现当前删除的点在原树上是当前是黑色的,则说明不合法。
代码:
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int MAXN=1e6+50;
struct Edge
{
int x,y,Next;
}e[MAXN<<1],e1[MAXN];
int elast[MAXN],tot,e1last[MAXN],tot1;
void Add1(int x,int y)
{
tot++;
e[tot].x=x;
e[tot].y=y;
e[tot].Next=elast[x];
elast[x]=tot;
}
bool Use[MAXN];
void Add2(int x,int y)
{
Use[x]=Use[y]=true;
tot1++;
e1[tot1].x=x;
e1[tot1].y=y;
e1[tot1].Next=e1last[x];
e1last[x]=tot1;
}
priority_queue<int,vector<int>,greater<int> >q;
int N;
char Color[MAXN];
int father[MAXN];
bool Can[MAXN];
int Deg[MAXN];
void dfs1(int u,int fa)
{
father[u]=fa;
Can[u]=(Color[u]=='W');
for(int i=elast[u];i;i=e[i].Next)
{
int v=e[i].y;
if(v==fa)
continue;
dfs1(v,u);
if(Can[v]==false)
{
Add2(u,v);
Deg[v]++;
}
else
{
Add2(v,u);
Deg[u]++;
Can[u]^=1;
}
}
}
vector<int>ans;
int main()
{
scanf("%d",&N);
for(int i=1;i<N;i++)
{
int x,y;
scanf("%d%d",&x,&y);
Add1(x,y);
Add1(y,x);
}
scanf("%s",&Color[1]);
dfs1(1,0);
for(int i=1;i<=N;i++)
{
if(Deg[i]==0)
{
q.push(i);
}
}
while(!q.empty())
{
int u=q.top();
q.pop();
if(Color[u]=='B')
{
puts("-1");
return 0;
}
ans.push_back(u);
for(int i=elast[u];i;i=e[i].Next)
{
int v=e[i].y;
if(Color[v]=='W')
Color[v]='B';
else
Color[v]='W';
}
for(int i=e1last[u];i;i=e1[i].Next)
{
int v=e1[i].y;
Deg[v]--;
if(Deg[v]==0)
{
q.push(v);
}
}
}
if(ans.size()!=N)
{
puts("-1");
}
else
{
for(int i=0;i<ans.size();i++)
{
printf("%d ",ans[i]);
}
}
}
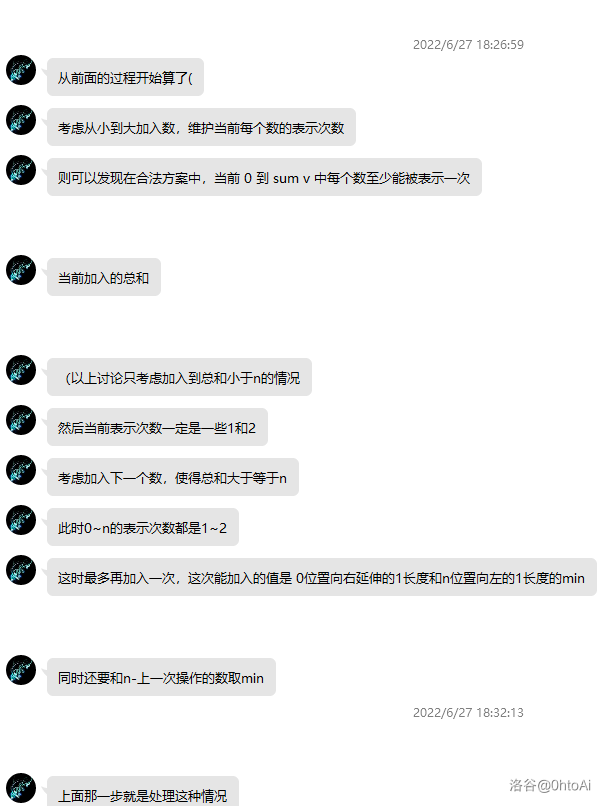
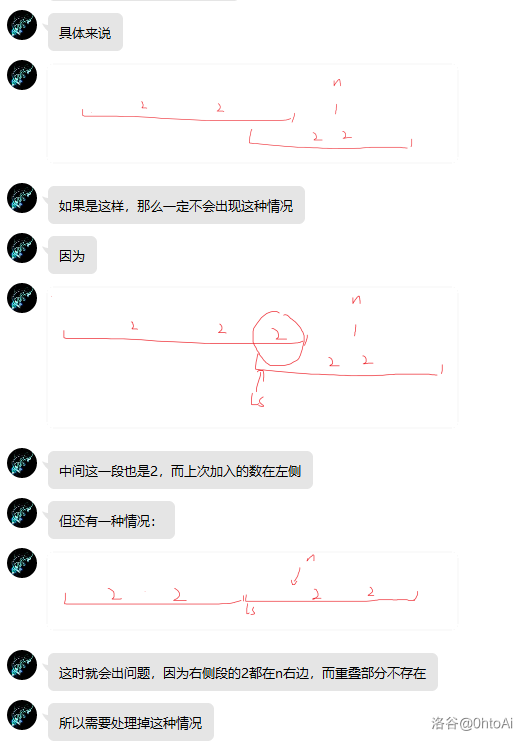
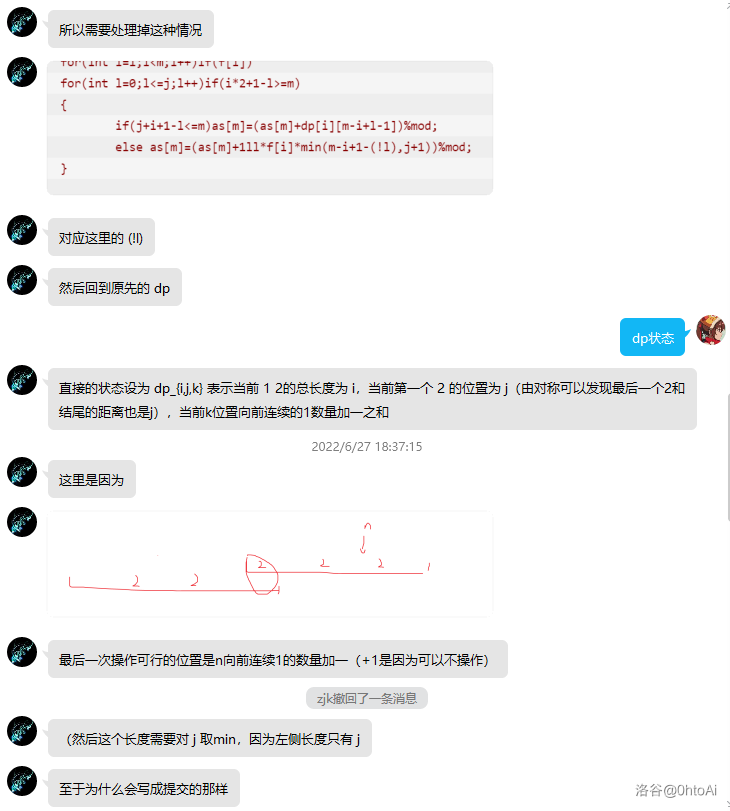
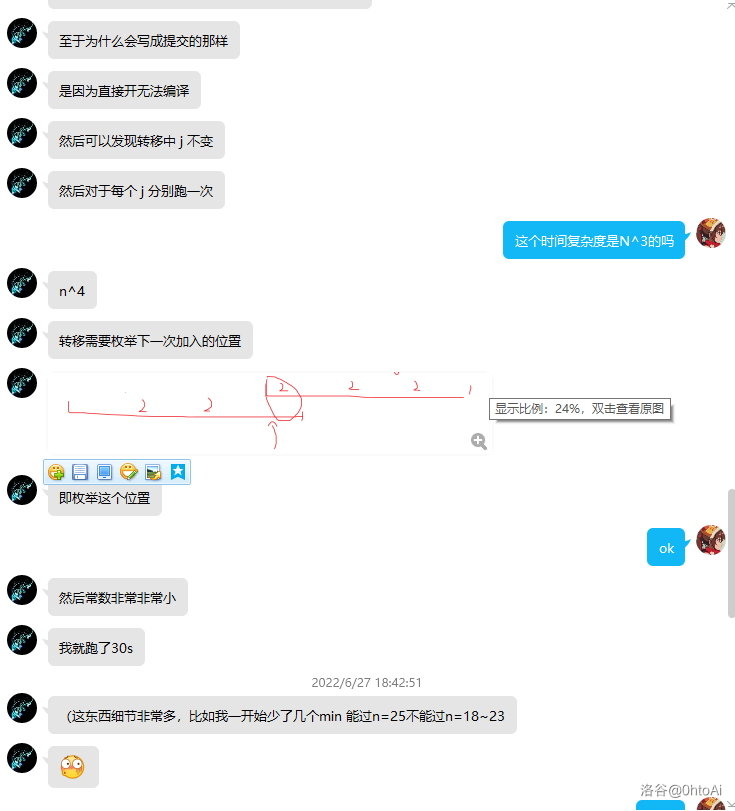
F - Counting Subsets
贴一份zjk的做法。暂时没做。
本文来自博客园,作者:0htoAi,转载请注明原文链接:https://www.cnblogs.com/0htoAi/p/16415701.html



