希尔伯特曲线python3实现

 

 

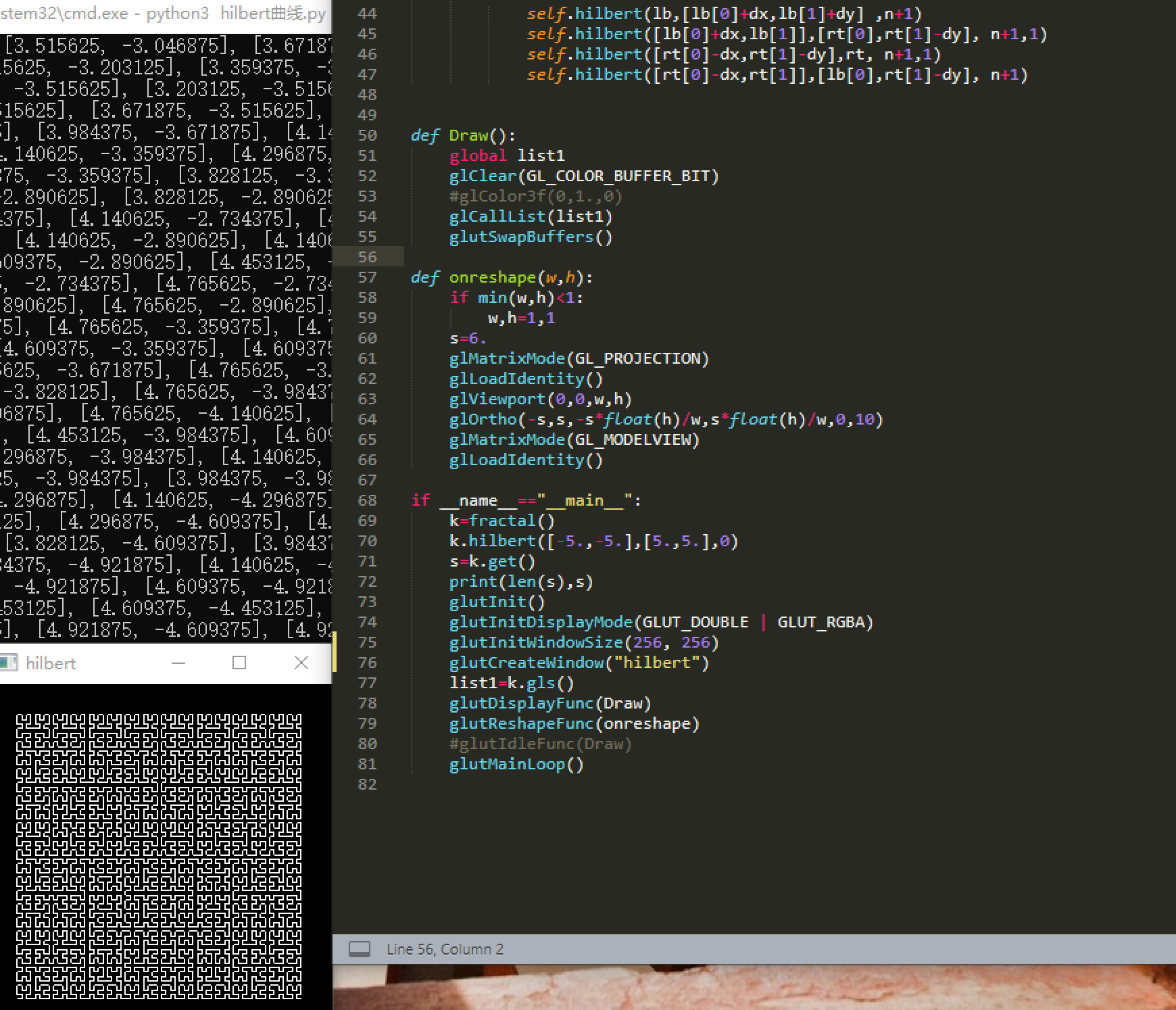
需要OpenGL库：https://www.lfd.uci.edu/~gohlke/pythonlibs/#pyopengl

#coding:utf-8
from OpenGL.GL import *
from OpenGL.GLUT  import *
class fractal(object):
    def __init__(self):
        self.points=[]
    
    def get(self):
        return self.points
    def gls(self):
        list1=glGenLists(1)
        glNewList(list1,GL_COMPILE)
        glBegin(GL_LINE_STRIP)
        for l in self.points:
            glVertex2fv(l)
        glEnd()    
        glEndList() 
        return list1
    def hilbert(self,lb,rt,n,tr=0):
        if n==5:
            if tr:
                dx=(rt[0]-lb[0])/4.
                dy=(rt[1]-lb[1])/4.
                self.points.append([lb[0]+dx,lb[1]+dy])
                self.points.append([lb[0]+3*dx,lb[1]+dy])
                self.points.append([rt[0]-dx,rt[1]-dy])
                self.points.append([lb[0]+dx,lb[1]+3*dy])                
                return
            dx=(rt[0]-lb[0])/4.
            dy=(rt[1]-lb[1])/4.
            self.points.append([lb[0]+dx,lb[1]+dy])
            self.points.append([lb[0]+dx,lb[1]+3*dy])
            self.points.append([rt[0]-dx,rt[1]-dy])
            self.points.append([lb[0]+3*dx,lb[1]+dy])
            return 
        dx=(rt[0]-lb[0])/2.
        dy=(rt[1]-lb[1])/2.
        if not tr:
            self.hilbert(lb,[lb[0]+dx,lb[1]+dy] ,n+1,1)
            self.hilbert([lb[0],lb[1]+dy],[rt[0]-dx,rt[1]], n+1)
            self.hilbert([rt[0]-dx,rt[1]-dy],rt, n+1)
            self.hilbert([rt[0],rt[1]-dy],[rt[0]-dx,lb[1]], n+1,1)
        if tr:
            self.hilbert(lb,[lb[0]+dx,lb[1]+dy] ,n+1)
            self.hilbert([lb[0]+dx,lb[1]],[rt[0],rt[1]-dy], n+1,1)
            self.hilbert([rt[0]-dx,rt[1]-dy],rt, n+1,1)
            self.hilbert([rt[0]-dx,rt[1]],[lb[0],rt[1]-dy], n+1)            
   
        
def Draw():
    global list1
    glClear(GL_COLOR_BUFFER_BIT)
    #glColor3f(0,1.,0)
    glCallList(list1)
    glutSwapBuffers()
 
def onreshape(w,h):
    if min(w,h)<1:
        w,h=1,1
    s=6.
    glMatrixMode(GL_PROJECTION)
    glLoadIdentity()
    glViewport(0,0,w,h)
    glOrtho(-s,s,-s*float(h)/w,s*float(h)/w,0,10)
    glMatrixMode(GL_MODELVIEW)
    glLoadIdentity()
 
if __name__=="__main__":
    k=fractal()
    k.hilbert([-5.,-5.],[5.,5.],0)
    s=k.get()
    print(len(s),s)
    glutInit()
    glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGBA)
    glutInitWindowSize(256, 256)
    glutCreateWindow("hilbert")
    list1=k.gls()
    glutDisplayFunc(Draw)
    glutReshapeFunc(onreshape)
    #glutIdleFunc(Draw)
    glutMainLoop()