简单基础数论

目录

• 欧几里得算法
• 素数筛
  • Eratosthenes筛
  • 前置
  • 筛法
  • 时间复杂度分析
  • 代码
  • 线性筛
• 扩展欧几里得算法
  • 问题
  • 分析
  • 例题（线性同余方程组）
• 乘法逆元
  • 介绍
  • 方法1（扩欧）
  • 方法2（费马小定理）
• 欧拉函数
  • 定义
  • 性质
  • 单个求法
  • 筛法求表
  • 欧拉定理

欧几里得算法

直接上代码

#include <bits/stdc++.h>
using namespace std;
int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}
int main()
{
    int a, b;
    cin >> a >> b;
    cout << gcd(a, b);
    return 0;
}

欧几里得算法是经典的最常用的辗转相除法求最大公因数。
下面我们思考为何辗转相除是正确的。
假设

\[g = gcd(a, b), a = mg, b=ng \]

显然，m与n互素（没有共同因数），通过辗转相除，我们得到新的a1，b1

\[a1 = b = ng, b1 = a \% b = (m\%n)g = kg \]

不断取模辗转相除最终可以得到某个数变为了0，得到(g, 0)。
那为什么不会得到(2g,0)、(3g,0)呢？因为在辗转相除的过程中，最开始的系数m、n互素，所以后面每对系数都是互素的，若有不互素情况，说明g不是gcd(a,b)。（说的有点拗口，难理解可以通过更相减损进行推导模拟）

素数筛

Eratosthenes筛

前置

1.若x是素数，那么kx(k>1)一定不是素数。
2.非素数N的因子可以分为两组[2,\(\sqrt{N}\)]和[\(\sqrt{N}\), N],每个N在[2, \(\sqrt{N}\)]的因子，一定能在[\(\sqrt{N}\), N/2]上找到对应因子。

筛法

根据第一条，筛法就是素数的倍数，而且对于某个素数x和他的倍数kx，如果\(kx < x^2\),那么kx一定被其他更小的素数筛掉过了
根据第二条，我们要得到[2, N]的素数表，我们只要在[2,\(\sqrt{N}\)]中用素数去筛掉非素数。

时间复杂度分析

厄拉多塞筛法的时间复杂度为O(NloglogN)。
考虑筛法，是对于每个素数筛除倍数。因此筛的次数为

\[\sum_{p\le\sqrt N\ }\frac{N}{p}=O\left(NloglogN\right) \]

代码

for (int i = 2; i * i <= n; ++i)
    {
        if (!not_prime[i])
        {
            for (int j = i * i; j <= n; j += i)
                not_prime[j] = 1;
        }
    }

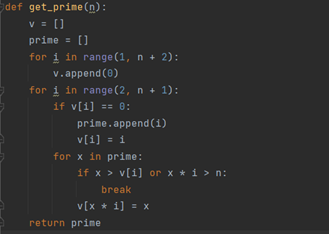
线性筛

厄拉多塞筛中有些数被重复筛除。因此我们考虑将每个合数只被他最小素因子筛掉的方法。
对于每个数记录一个最小素因子，每个数筛后面的数的时候，都乘比这个最小素因子小的素数。
复杂度O（N）

扩展欧几里得算法

问题

求\(ax+by=gcd(a,b)\)的解(x,y)。（裴蜀定理）

分析

我们知道\(gcd(a,b)=gcd(b,a\%b)\)，那么让我们考虑另一个方程：\(bx_1+(a\%b)y_1=gcd(b,a\%b)\)
若能得到x1和y1,那么通过等式和a%b=a-(a/b)*b我们也能得到

\[(x,y) = (y_1,x_1-(a/b)y_1) \]

考虑辗转相除法的过程，一直进行下去会得到

\[ax_n+0y_n = gcd(a,0) = a \]

一组解便是\(xn=1,yn=0\),反推回去得到一组(x,y)。
考虑其他解(m,n)

\[a(m-x) + b(n - y) = 0 \]

同除gcd(a,b)可以得到c=a/g,d=b/g,显然c、d互素。

\[c(m-x)+d(n-y)=0 \]

由于cd互素，那么

\[m-x=kd,n-y=-kc(k不定) \]

其中k不定，我们枚举k，那么

\[(m,n)=(x+b/g*k,y-a/g*k) \]

例题（线性同余方程组）

洛谷 青蛙的约会

//青蛙约会
#include <bits/stdc++.h>
using namespace std;
#define LL long long
LL k_gcd(LL a, LL b, LL &x, LL &y)
{
    if (!b)
    {
        x = 1, y = 0;
        return a;
    }
    LL d = k_gcd(b, a % b, y, x);
    y -= x * (a / b);
    return d;
}
int main()
{
    LL x, y, m, n, l, a, b, c, t, k;
    //(m - n)t + lk = y - x, find positive min t
    cin >> x >> y >> m >> n >> l;
    if (m - n < 0)
        a = n - m, c = x - y;
    else
        a = m - n, c = y - x;
    b = l;
    LL g = k_gcd(a, b, t, k);
    if (c % g)
        cout << "Impossible";
    else
    {
        t = t * (c / g);
        cout << (t % (b / g) + b / g) % (b / g);
    }
    return 0;
}

乘法逆元

介绍

乘法逆元相当于是在模意义下将除法转化成乘法。

\[ax \equiv 1 \pmod b \]

在模b意义下x就是a的倒数，求解这个同余方程可以得到x，得到a的逆元。

方法1（扩欧）

用扩展欧几里得算法求解同余方程，得到x。
不多说。
注意限制：

\[gcd(a,b) = 1 \]

方法2（费马小定理）

直接来说就是：

\[x \equiv a^{b-2} \]

限制：b为素数, gcd(a, b) = 1

#include <bits/stdc++.h>
using namespace std;
#define b 23333
int fast_pow(int a, int k)
{
    int ans = 1;
    while (k)
    {
        if (k & 1)
            ans = 1ll * ans * a % b;
        a = a * a % b;
        k >>= 1;
    }
    return ans;
}
int main()
{
    int a;
    cin >> a;
    cout << fast_pow(a, b - 2);
    return 0;
}

欧拉函数

定义

欧拉函数 \(\phi (n)\)表示小于等于n的数里面与n互质的个数
其中\(\phi(1) = 1\), 如果 n 为质数， \(\phi(n) = n - 1\)

性质

1. 积性函数
   如果\(gcd(a,b) = 1\), 那么\(\phi(a*b)=\phi(a)*\phi(b)\)
2. \(n = \sum_{d|n} \phi(d)\)
   证明：考虑gcd(k,n)

\[\sum_{1<=i<=n}cnt(gcd(k,n)=i)=n \]

又由于

\[gcd(k,n)=i,gcd(\frac ki, \frac ni) = 1 \]

所以上式可以推导为

\[\sum_{d|n}cnt(gcd(k,d)=1)=n \]

其中cnt(gcd(k,d)=1)就是\(\phi(d)\)
得证！(利用莫比乌斯反演相关知识也可得出)
3. 若 \(n = p^k\) ,p为质数，那么\(\phi(n)=p^k-p^{k-1}\)
证明：n的基本因数为p,那么p*a与n不互素，其中a取遍整数区间[1,p^k-1]
4. 若\(n=\prod_{i=1}^sp_i^{k_i}\) 那么 \(\phi(n)=n*\prod_{i=1}^s \frac{p_i-1}{p_i}\)
证明：拿性质3和性质1得到。

单个求法

利用性质4，唯一分解定理推出。

int phi(int x)
{
    int ans = x;
    for (int i = 2; i * i <= x; ++i)
    {
        if (x % i == 0)
        {
            ans = ans / i * (i - 1);
            while (x % i == 0)
                x /= i;
        }
    }
    if (x > 1)
        ans = ans / x * (x - 1);
    return ans;
}

筛法求表

唯一分解定律，每个数会被他的每个质数因子筛一次。

void phi_make()
{
    phi[1] = 1;
    for (int i = 2; i <= 23333; ++i)
    {
        if (!phi[i])
            for (int j = i; j <= 23333; j += i)
            {
                if (!phi[j])
                    phi[j] = j;
                phi[j] = phi[j] / i * (i - 1);
            }
    }
}

欧拉定理

若\(gcd(a,m)=1\), 则\(a^{\phi(m)} \equiv1 \pmod m\)