HashMap源码阅读(二)
了解HashMap中的红黑树
红黑树定义: 红黑树是一种含有红黑节点并能自平衡的二叉查找树。它必须满足下面性质:
性质1:每个节点要么是黑色,要么是红色
性质2:根节点是黑色
性质3:每个叶子节点(NIL)是黑色
性质4:每个红色节点的两个子节点一定是黑色
性质5:任意一节点到每个叶子节点的路径都包含数量相同的黑节点
HashMap中的树节点结构
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
TreeNode<K,V> parent; // 父节点
TreeNode<K,V> left; // 左孩子节点
TreeNode<K,V> right; //右孩子节点
// 前驱节点,还有一个next域表示后继节点,这两个节点主要用在树形化和反树形化过程中。
TreeNode<K,V> prev;
boolean red;// 红黑状态标志
TreeNode(int hash, K key, V val, Node<K,V> next) {
super(hash, key, val, next);
}
LinkedHashMap中节点结构,主要比普通节点多了before和after域用于记录节点的顺序(插入顺序或者访问顺序)
static class Entry<K,V> extends HashMap.Node<K,V> {
Entry<K,V> before, after;
Entry(int hash, K key, V value, Node<K,V> next) {
super(hash, key, value, next);
}
}
普通节点, 包含键的hash值, 键, 值, next指针
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next;
树中的调整操作
树需要通过左旋,右旋,变色等操作来转换为满足条件的红黑色。
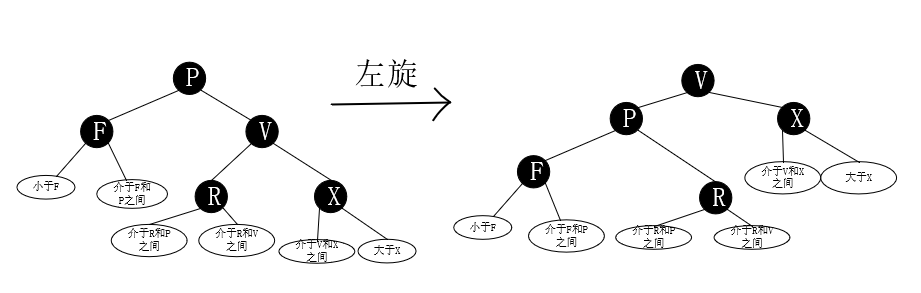
左旋:以某个节点作为旋转节点,其右子节点变为旋转节点的父节点,右子节点的左子节点变为旋转节点的右子节点。如下图P节点的左旋操作
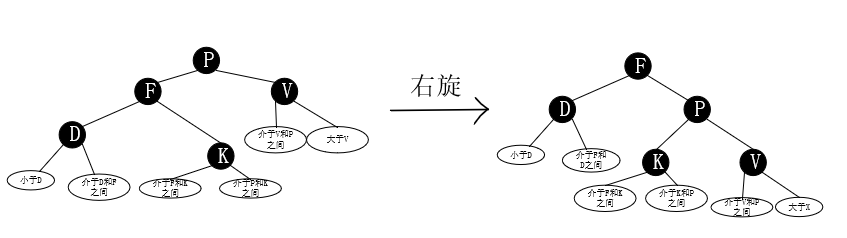
右旋:以某个节点作为旋转节点,其左子节点变为旋转节点的父节点,左子节点的右子节点变为旋转节点的左子节点。
变色:变为红色或者黑色。
// HashMap中左旋代码, 以p为旋转点进行左旋操作
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,
TreeNode<K,V> p) {
// pp 为p的父节点, r为p的右孩子, rl为p的右孩子的左孩子
TreeNode<K,V> r, pp, r1;
// r 表示旋转点的右孩子
if (p != null && (r = p.right) != null) {
// 把旋转点右孩子的左孩子变为旋转点的右孩子
if ((rl = p.right = r.left) != null)
// 设置相应节点的父节点
rl.parent = p;
//设置旋转点右孩子地父节点为旋转点地父节点
if ((pp = r.parent = p.parent) == null)
// 如果旋转点没有父节点,即旋转点为根节点,那么根节点只能为黑色。
(root = r).red = false;
// 旋转点为其父节点地左孩子, 设置其父节点地左孩子是选转点地右孩子
else if (pp.left == p)
pp.left = r;
else // 如果是其父节点地右孩子
pp.right = r;
// 设置旋转点为其右孩子的左孩子节点
r.left = p;
// 设置旋转点的父节点为其右孩子节点
p.parent = r;
}
return root;
}
右旋案例
// 右旋代码分析
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,
TreeNode<K,V> p) {
TreeNode<K,V> l, pp, lr;
// l表示旋转点的p的左孩子
// lr 表示旋转点p的左孩子的右孩子
// pp 表示旋转点p的父节点
if (p != null && (l = p.left) != null) {
// 把旋转点左孩子的右孩子设置为旋转点的左孩子
if ((lr = p.left = l.right) != null)
//重新设置相应的父节点为旋转点p
lr.parent = p;
// 旋转点p的父节点设置为旋转点p的左孩子的父节点,
if ((pp = l.parent = p.parent) == null)
// 父节点为空,表示旋转点是根节点, 所以需要把它的左孩子颜色设置为黑色
(root = l).red = false;
// 旋转点是父节点的右孩子
else if (pp.right == p)
// 旋转之后的节点l依然是父节点的右孩子
pp.right = l;
else
pp.left = l;
//l的右孩子变为旋转点
l.right = p;
//设置旋转点的父节点
p.parent = l;
}
return root;
}
红黑树的插入
插入操作分为两步, 第一步查找, 第二部插入后红黑色的调整。
//查找函数分析
/**
* 以当前节点p开始查找hash值为h, 键为k, kc表示comparableClassFor(k)返回的类型
*
* 返回null表示没有查找到相应的元素。
* 第一步比较hash值
* 如果p的hash值小于h, 往p的右孩子节点查找
* 如果p的hash值大于h, 往p的左孩子节点查找
* 如果p的hash值等于h, 看key是否相等?
* 如果key相等,直接返回当前节点。
* 如果key不相等, 判断左右孩子节点是否为空, 左孩子为空就设置右孩子为当前节点,右孩子为空则设置左孩子
* 如果左右孩子都不为空, 判断key是否可以比较大小。即是否实现Comparable接口
* 如果key实现Comparable接口,那么利用Comparable来选择是左孩子还是右孩子设置为当前节点开始进一步查找
* 如果key没实现此接口, 那么先从右孩子节点开始查找,没找到再从左孩子节点开始查找。
*
*/
final TreeNode<K,V> find(int h, Object k, Class<?> kc) {
TreeNode<K,V> p = this;
do {
int ph, dir; K pk;
TreeNode<K,V> pl = p.left, pr = p.right, q;
if ((ph = p.hash) > h)
p = pl;
else if (ph < h)
p = pr;
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
return p;
else if (pl == null)
p = pr;
else if (pr == null)
p = pl;
// 利用Compare方法比较大小
else if ((kc != null ||
(kc = comparableClassFor(k)) != null) &&
(dir = compareComparables(kc, k, pk)) != 0)
p = (dir < 0) ? pl : pr;
// 先查右孩子, 再查左孩子
else if ((q = pr.find(h, k, kc)) != null)
return q;
else
p = pl;
} while (p != null);
return null;
}
插入数据总体流程分为两步
第一步:查找相应的插入位置,
如果存在hash值相等,key不可比较且搜索标志searched为false,那么深度搜索遍历整个红黑树。查找是否存在和插入节点相等的节点,存在直接返回,不存在设置搜索状态标志searched为true, 并调用tieBreakOrder方法来判断两个hash值相等且键不可以比较的节点数据大小。(只会进行一次深搜)
第二步:插入节点,并自适应平衡红黑树(插入的节点需要维护相应的next和prev指针)
// 插入数据时,在桶中第一个元素为树节点时,调用putTreeVal方法插入数据
/**
** h 表示需要插入节点的hash值
** k 表示相应的键
** v 表示相应的值
**/
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
int h, K k, V v) {
Class<?> kc = null;
// 搜索状态标志
boolean searched = false;
// 获取红黑树的根节点
TreeNode<K,V> root = (parent != null) ? root() : this;
// 第一步开始查找hash值为h, key为k, value 为v的节点插入位置
for (TreeNode<K,V> p = root;;) {
int dir, ph; K pk;
// 说明插入的位置在p的左边
if ((ph = p.hash) > h)
dir = -1;
// 说明插入的位置在p的右边
else if (ph < h)
dir = 1;
// 需要插入的键已经存在,直接返回
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
return p;
// 对于hash值相等情况,看相应key是否可以比较大小 ,满足下面条件表示不可以比较大小
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0) {
if (!searched) {
TreeNode<K,V> q, ch;
// 标识只进行一次深度优先查找, 因为一次就知道结果。
searched = true;
// 深度优先遍历查找
if (((ch = p.left) != null &&
(q = ch.find(h, k, kc)) != null) ||
((ch = p.right) != null &&
(q = ch.find(h, k, kc)) != null))
return q;
}
// 对于那些哈希值相同但不可比较的元素排序规则
dir = tieBreakOrder(k, pk);
}
// 第二个步骤, 依据第一个步骤查找过程中的dir值,来进行左右孩子的选择
TreeNode<K,V> xp = p;
// 表明相应左孩子或者右孩子为null, 可以插入到此位置
if ((p = (dir <= 0) ? p.left : p.right) == null) {
// 当前节点的下一个节点
Node<K,V> xpn = xp.next;
// 新创建一个树形节点, next值为原来p的next
TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);
// 设置左右孩子
if (dir <= 0)
xp.left = x;
else
xp.right = x;
// 设置next 和prev
xp.next = x;
x.parent = x.prev = xp;
if (xpn != null)
((TreeNode<K,V>)xpn).prev = x;
// 插入之后的元素平衡调整, moveRootToFront方法调整桶中的第一个元素为红黑树的根节点
moveRootToFront(tab, balanceInsertion(root, x));
return null;
}
}
}
// 插入元素之后的平衡操作,
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
TreeNode<K,V> x) {
// xp 表示插入节点的父节点
// xpp表示插入节点的祖父节点
// xppl,xppr 表示插入节点的父节点或者兄弟节点
x.red = true; // 一般设置插入元素的颜色为红色,避免违反黑色完美平衡原则
for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
// 情景1 x是根节点, 设置颜色为黑色并返回。
if ((xp = x.parent) == null) {
x.red = false;
return x;
}
// 情景2. 插入节点的父节点为黑色, 并不影响红黑树的平衡
else if (!xp.red || (xpp = xp.parent) == null)
return root;
// 情景3. 插入节点的父节点为红色,
// 情景3.1 插入节点的父节点为祖父节点的左孩子
if (xp == (xppl = xpp.left)) {
// 3.1.1 叔叔节点存在,并且为红节点, 那么情况就是黑红红, 变为红黑黑
// 如果xpp的父节点为红色,那么把xpp看作插入节点进行平衡操作
if ((xppr = xpp.right) != null && xppr.red) {
xppr.red = false;
xp.red = false;
xpp.red = true;
// 把xpp看作新的插入节点,进行平衡操作
x = xpp;
}
else {// 3.1.2 叔叔节点不存在或者为黑节点,
//3.1.2.1 插入节点是其父节点的右子节点
if (x == xp.right) {
//先对p节点进行左旋, 接着把p设置为插入节点x = xp得到情景3.2.2
root = rotateLeft(root, x = xp);
// 重新获取父节点xp和祖父节点xpp
xpp = (xp = x.parent) == null ? null : xp.parent;
}
// 3.1.2.2 插入节点是其父节点的左子树
// 将p设置为黑色, 将pp设置为红色, pp进行右旋
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateRight(root, xpp);
}
}
}
}
else {// 3.2 插入节点的父节点是祖父节点的右孩子,
//3.2.1 插入节点的叔叔节点存在且为红色
if (xppl != null && xppl.red) {
// 叔叔节点变为黑色, 父节点变为黑色, 祖父节点变为红色
// 把xpp作为新的插入单元,进行调整
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
else {// 3.2.2 插入节点的叔叔节点不存在或者为黑色
// 3.2.2.1 插入节点是父节点的左孩子
if (x == xp.left) {
// 以父节点进行右旋操作, 设置插入点为父节点, 接着如3.3.2.2
root = rotateRight(root, x = xp);
// 更新父节点及祖父节点
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {// 3.3.2.2 插入节点为父节点的右子树
// 把父节点变成黑色, 把祖父节点变成红色, 以祖父节点为旋转点左旋。
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateLeft(root, xpp);
}
}
}
}
}
}
// balanceInsertion方法具体逻辑如下图

情景3.1.1 插入节点的父节点xp为红色, 插入节点的父节点xp是祖父节点xpp的左孩子, 插入节点的叔叔节点xppr存在并且为红节点 , 具体案例如下图
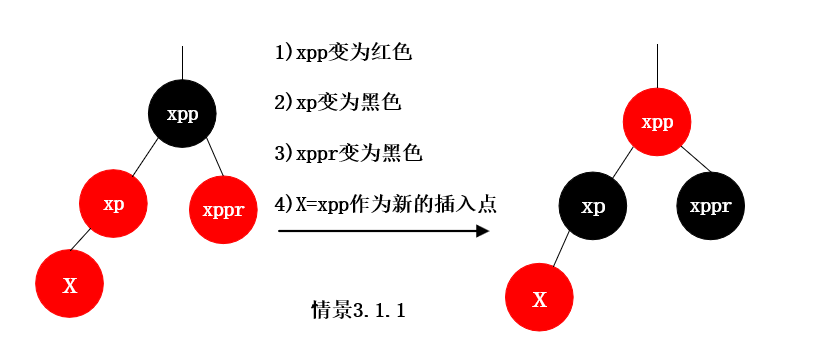
情景3.1.2.1 插入节点的父节点为红色, 插入节点的父节点是祖父节点的左孩子, 插入节点的叔叔节点不存在或者为黑节点, 插入节点是其父节点的右子树

情景3.1.2.2 插入节点的父节点为红色, 插入节点的父节点是祖父节点的左孩子, 插入节点的叔叔节点不存在或者为黑节点, 插入节点是其父节点的左子树
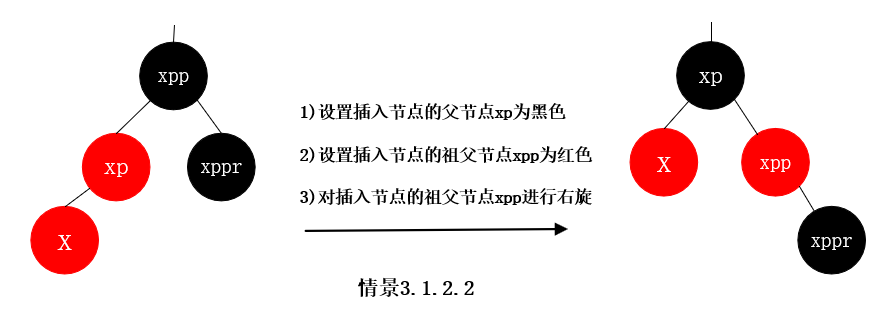
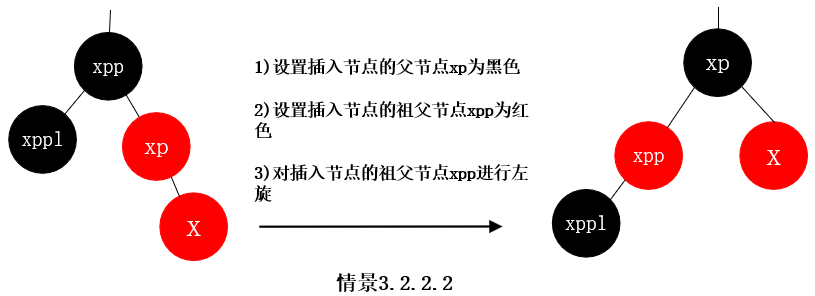
情景3.2.1 插入节点的父节点为红色, 插入节点的父节点是祖父节点的右孩子, 插入节点的叔叔节点存在且为红色
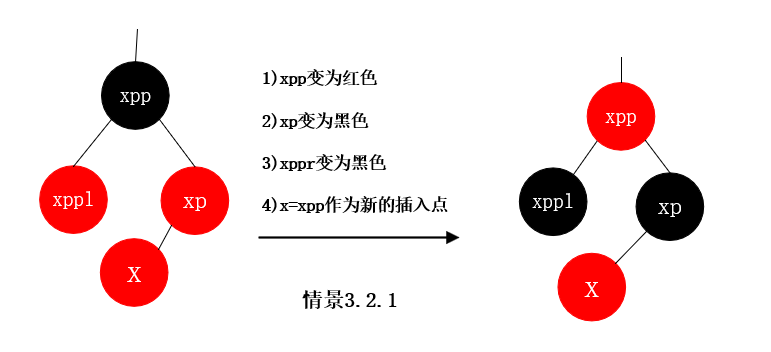
情景3.2.2.1 插入节点的父节点为红色, 插入节点的父节点是祖父节点的右孩子, 插入节点的叔叔节点不存在或者为黑节点, 插入节点x是其父节点xp的左孩子
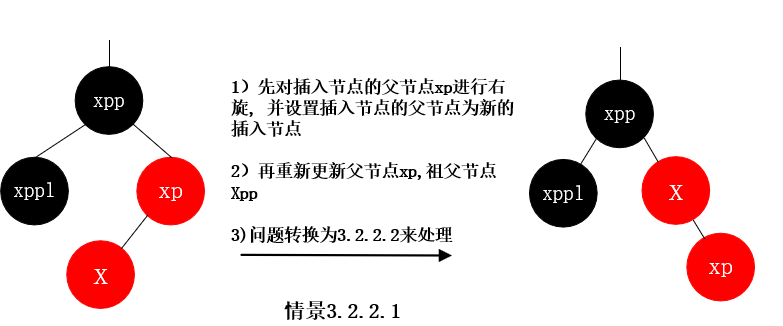
情景3.2.2.2 插入节点的父节点为红色, 插入节点的父节点是祖父节点的右孩子, 插入节点的叔叔节点不存在或者为黑节点, 插入节点x是其父节点xp的右孩子
// 插入节点x插入完成后, 经过平衡调整可能出现根节点的变动,比如原来桶中的节点不再是根节点。需要调用moveRootToFornt来调整桶中根节点。
/**
* 确保root就是散列桶中第一个元素. 首先判断树的根节点和散列桶中的第一个元素是否相等
* 如果不相等, 说明需要调整根节点为散列桶第一个元素, 先把树根节点从双向链表指针next和prev中释放出来,然后再用next和prev连接散列桶第一个元素和红黑树的根节点。
*/
static <K,V> void moveRootToFront(Node<K,V>[] tab, TreeNode<K,V> root) {
int n;
if (root != null && tab != null && (n = tab.length) > 0) {
int index = (n - 1) & root.hash;
TreeNode<K,V> first = (TreeNode<K,V>)tab[index];
if (root != first) { // 不相等, 说明平衡调整的过程中散列桶第一个元素改变啦。
Node<K,V> rn;
// 设置第一个元素为root
tab[index] = root;
// root节点的前驱
TreeNode<K,V> rp = root.prev;
// root节点的后继
if ((rn = root.next) != null)
// 前驱和后继关联
((TreeNode<K,V>)rn).prev = rp;
if (rp != null)
rp.next = rn;
// 设置first的前驱
if (first != null)
first.prev = root;
root.next = first;
// 根节点没有前驱
root.prev = null;
}
assert checkInvariants(root);
}
}
红黑树的删除操作包含三种情景
情景1:若删除节点无子节点,直接删除。
情景2:若删除节点只有一个子节点,用子节点替换删除节点。
情景3:若删除节点有两个子节点,用后继节点(大于删除节点的最小节点)替换删除节点。
删除思想:删除节点被替代后,再不考虑节点的键值的情况下,对于树来说,可以认为删除的是替代节点。如下图所示,再不看键值对的情况下,图中最终结果是删除Q所在的位置。

基于上面所说的三种删除情景可以相互转化并且最终都是转换为情景1
情景2:删除节点用其唯一的子节点替换为删除节点后,可以认为删除的是子节点,若子节点又有两个子节点,那么相当于转换为情景3,一直自定向下转换,总是能转换为情景1
情景3:删除节点用后继节点,如果后继节点有右子树,那么相当于转换为情景2,否则情景1。
删除树节点方法分析
第一步: 当前节点脱离双向链表, 使当前节点删除后,不影响整个双向链表中的next和pre
第二步: 当前节点脱离红黑树,即修改相应的left和right孩子指针
首先按照不同的情景1,2,3,找到删除节点p对应的替换节点replacement, 对于情景2 替换节点就是删除节点中不为null的子节点。对于情景3, 如果后继节点有右子树, 转换为情景2,替换节点就是右子节点, 否则变为情景1, 替换节点和删除节点重合。
如果替换节点和删除节点没重合,先用替换节点替换删除节点再执行平衡红黑树操作。否则, 直接执行红黑树平衡操作,最后再删除掉替换节点。
final void removeTreeNode(HashMap<K,V> map, Node<K,V>[] tab,
boolean movable) {
int n;
// 散列桶数组未初始化
if (tab == null || (n = tab.length) == 0)
return;
//散列到哪个桶
int index = (n - 1) & hash;
TreeNode<K,V> first = (TreeNode<K,V>)tab[index], root = first, rl;
TreeNode<K,V> succ = (TreeNode<K,V>)next, pred = prev;
// 如果要删除的节点是根节点, 那么直接设置删除节点的后继为新的根节点
if (pred == null)
tab[index] = first = succ;
else // 设置删除节点的前驱节点的后继节点为删除节点的后继
pred.next = succ;
// 设后继节点的前驱为删除节点的前驱
if (succ != null)
succ.prev = pred;
// 如果散列桶只有删除节点一个元素, 直接返回
if (first == null)
return;
// 找出桶中的真实根节点
if (root.parent != null)
root = root.root();
// 如果散列桶中元素个数太少, 把树形结构转换为普通链表结构
if (root == null
|| (movable
&& (root.right == null
|| (rl = root.left) == null
|| rl.left == null))) {
tab[index] = first.untreeify(map); // too small
return;
}
// 上面主要是当前节点脱离双链表, 下面是当前节点脱离红黑树
// p 当前节点, pl 当前节点的左孩子节点(简称左孩子),
// pr当前节点的右孩子节点(右孩子), replacement 替换节点
TreeNode<K,V> p = this, pl = left, pr = right, replacement;
// 左右孩子节点都不为空, 问题是情景3
if (pl != null && pr != null) {
TreeNode<K,V> s = pr, sl;
// 情景3采取措施找到后继节点, 替换删除节点
while ((sl = s.left) != null) // find successor
s = sl;
// 交换删除节点p和替换节点s的颜色
boolean c = s.red; s.red = p.red; p.red = c; // swap colors
// 保存替换节点s的右孩子
TreeNode<K,V> sr = s.right;
// 保存当前节点的父节点
TreeNode<K,V> pp = p.parent;
// 删除节点的右孩子节点pr没有左孩子节点, 则 删除节点的父指针指向右孩子节点s,右孩子节点的右指针指向当前节点
if (s == pr) { // p was s's direct parent
p.parent = s;
s.right = p;
}
else { // 当前节点的右孩子节点有左孩子
TreeNode<K,V> sp = s.parent;
// 当前节点的父指针指向s的父节点
if ((p.parent = sp) != null) {
// s是其父节点的左孩子, s的父节点sp的左指针指向当前节点
if (s == sp.left)
sp.left = p;
else
sp.right = p;
}
// s的右孩子为当前节点的右孩子
if ((s.right = pr) != null)
pr.parent = s;
}
// 上面都是右边调整, 下面开始当前节点的左边调整
p.left = null; // 当前节点的左孩子为null
// 当前节点的右孩子为s原来的右孩子sr
if ((p.right = sr) != null)
sr.parent = p;
// s的左孩子是原来p的左孩子
if ((s.left = pl) != null)
pl.parent = s;
// 设置pp的左孩子或右孩子,用s来替换p再pp中的位置
// 如果s的父节点不存在,则表明s是根节点
if ((s.parent = pp) == null)
root = s;
else if (p == pp.left)
pp.left = s;
else
pp.right = s;
// 找到替换点
if (sr != null)
replacement = sr;
else
replacement = p;
}
// 情景2, 删除节点只有一个子节点
else if (pl != null)
replacement = pl;
else if (pr != null)
replacement = pr;
else // 情景1, 删除节点没有子节点
replacement = p;
if (replacement != p) {
// 表明属于情景2,3情况, 删除p节点,并且更新pp的左右孩子节点
TreeNode<K,V> pp = replacement.parent = p.parent;
if (pp == null)
root = replacement;
else if (p == pp.left)
pp.left = replacement;
else
pp.right = replacement;
p.left = p.right = p.parent = null;
}
// 如果删除点p是红色,那么直接返回不需要平衡。否则平衡删除之后的树
// replacement可以就是删除节点, 也可以是删除节点的后继节点
TreeNode<K,V> r = p.red ? root : balanceDeletion(root, replacement);
if (replacement == p) { // 对于没有子树节点的删除,直接把此节点从树中分离就行
TreeNode<K,V> pp = p.parent;
p.parent = null;
if (pp != null) {
if (p == pp.left)
pp.left = null;
else if (p == pp.right)
pp.right = null;
}
}
if (movable)
moveRootToFront(tab, r);
}
删除元素之后的平衡操作

// root根节点, x表示替换节点, 这边的替换节点存在两种情况,
//第一种是替换节点和删除节点不重合, 那么删除节点已经被删除
// 第二种替换节点和删除节点重合, 那么删除节点目前还未被删除
static <K,V> TreeNode<K,V> balanceDeletion(TreeNode<K,V> root,
TreeNode<K,V> x) {
// xp 表示替换节点的父节点
// xpl, xpr表示替换节点的父节点或者叔叔节点
for (TreeNode<K,V> xp, xpl, xpr;;) {
// 表明删除之后的树结构为null, 或者根节点为x
if (x == null || x == root)
return root;
// 说明删除之后,x是根节点,直接把颜色设置为黑色
else if ((xp = x.parent) == null) {
x.red = false;
return x;
}
// 情况1.如果替换节点x的颜色为红色,
//由于p的颜色为黑色,因此替换节点需要保持和删除节点同一种颜色。
else if (x.red) {
x.red = false;
return root;
}
// 情况2.替换节点是黑色,
//情况2.1替换节点是其父节点的左子树
else if ((xpl = xp.left) == x) {
//情况2.1.1替换节点的兄弟节点是红节点
if ((xpr = xp.right) != null && xpr.red) {
xpr.red = false;
xp.red = true;
root = rotateLeft(root, xp);
xpr = (xp = x.parent) == null ? null : xp.right;
}
// 情况2.1.2 替换节点的兄弟节点不存在
if (xpr == null)// 替换节点的兄弟节点为null
x = xp;
else {
// 2.1.3 替换节点的兄弟节点不为null,且其颜色为黑色(为什么说是黑色,
//因为经过2.1.1的条件下,替换节点的兄弟节点一定为黑色)
TreeNode<K,V> sl = xpr.left, sr = xpr.right;
// 2.1.3.1替换节点的兄弟节点的子节点都为黑色
if ((sr == null || !sr.red) &&
(sl == null || !sl.red)) {
// 将替换节点的兄弟节点xpr颜色设置为红色
// 把x移动到xp, 即替换点的父节点作为新的替换节点
// 实际上是把x的黑色移动到xp上
xpr.red = true;
x = xp;
}
else {
// 2.1.3.2 替换节点的兄弟节点的右子节点是黑色,左子节点为红色
if (sr == null || !sr.red) {
// 将替换节点的兄弟节点的左子节点sl设置为黑色,
// 将替换节点的兄弟节点xpr设置为红色
//对xpr节点进行右旋
//更新xpr和xp信息
if (sl != null)
sl.red = false;
xpr.red = true;
root = rotateRight(root, xpr);
xpr = (xp = x.parent) == null ?
null : xp.right;
}
// 2.1.3.3 替换节点的兄弟节点的右子节点是红色, 左子节点任意颜色
// 兄弟节点xpr设置为父节点xp的颜色
// 兄弟节点的右孩子节点sr设置为黑色
//父节点xp设置为黑色
// 对xp进行左旋
if (xpr != null) {
xpr.red = (xp == null) ? false : xp.red;
if ((sr = xpr.right) != null)
sr.red = false;
}
if (xp != null) {
xp.red = false;
root = rotateLeft(root, xp);
}
x = root;
}
}
}
else { // symmetric 和上述步骤对称
// 2.2 替换节点是其父节点的右孩子
// 2.2.1 替换节点的兄弟节点是红色
if (xpl != null && xpl.red) {
// 将兄弟节点xpl设置为黑色
// 将父节点xp设置为红色
// 对父节点xp进行右旋操作
// 进行情景2.2.2.1的处理
xpl.red = false;
xp.red = true;
root = rotateRight(root, xp);
xpl = (xp = x.parent) == null ? null : xp.left;
}
// 2.2.2 兄弟节点不存在
if (xpl == null)// 无法理解为什么会出现这种情况??
x = xp;
else {// 2.2.3 替换节点的兄弟节点是黑色
TreeNode<K,V> sl = xpl.left, sr = xpl.right;
// 2.2.3.1 替换节点的兄弟节点的子节点都为黑色
if ((sl == null || !sl.red) &&
(sr == null || !sr.red)) {
// 将替换节点的兄弟节点设置为红色
// 将父节点射为新的替换节点
xpl.red = true;
x = xp;
}
else {
// 2.2.3.2 替换节点的兄弟节点的左节点为黑色, 右节点为红色
//将兄弟节点xpl设置为红色
// 将兄弟节点的右节点设置为黑色
//对兄弟节点xpl进行左旋
//得到情景2.2.3.3
if (sl == null || !sl.red) {
if (sr != null)
sr.red = false;
xpl.red = true;
root = rotateLeft(root, xpl);
xpl = (xp = x.parent) == null ?
null : xp.left;
}
// 2.2.3.3 替换节点的兄弟节点的左子节点为红色, 右子节点任意颜色
//将兄弟节点xpl的颜色设置为父节点Xp的颜色
//兄弟节点的左孩子sl的颜色设置为黑色
//父节点xp的颜色设置为黑色
//对父节点xp进行右旋
if (xpl != null) {
xpl.red = (xp == null) ? false : xp.red;
if ((sl = xpl.left) != null)
sl.red = false;
}
if (xp != null) {
xp.red = false;
root = rotateRight(root, xp);
}
x = root;
}
}
}
}
}
balanceDeletion删除元素之后的平衡调整案例
情况1: 删除节点为黑色,替换节点x的颜色为红色, 这表明替换点和删除不是同一个点,从而直接把替换点设置为黑色就好啦。
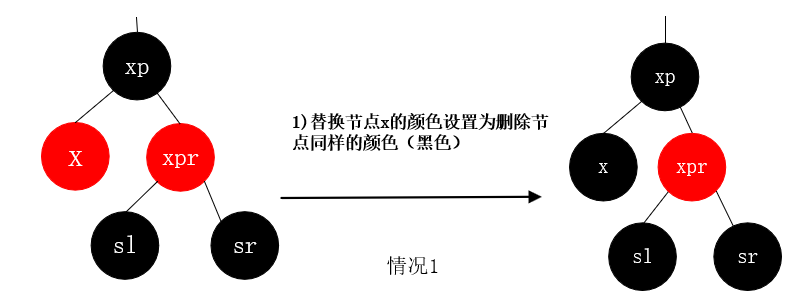
情况2.1.1: 删除节点为黑色, 替换节点是其父节点的左子树, 替换节点的兄弟节点是红节点。 我们需要向右边借一个节点来平衡删除节点之后的黑色不平衡。

情况2.1.2: 删除节点为黑色, 替换节点是其父节点的左子树,替换节点的兄弟节点不存在。我觉得这种情况不会出现,因为刚开始树是平衡或者相差一个黑节点的状态。我们假设下图中x替换点和删除点不重合, 那么原本的树会相差两个黑节点,不是平衡状态。因此假设无效。接着我们假设下图x替换点和删除点重合,那么下图应该是平很状态,显然下图不满足条件,因此假设无效。所以,不可能会存在这种状态???????好疑惑啊!!!!!!
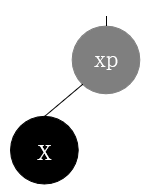
情况2.1.3.1:删除节点为黑色, 替换节点是其父节点的左子树, 替换节点的兄弟节点存在且颜色为黑色, 替换节点的兄弟节点的子节点都为黑色(可能不存在子节点,因为nil也是黑节点)
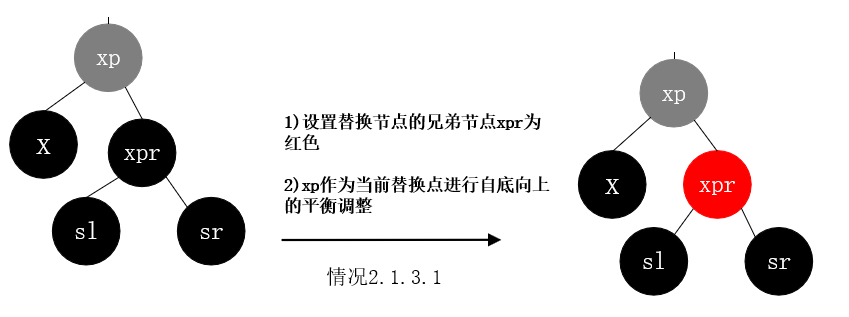
情况2.1.3.2: 删除节点为黑色, 替换节点是其父节点的左子树, 替换节点的兄弟节点存在且颜色为黑色, 替换节点的兄弟节点的右子节点是黑色 左子节点为红色
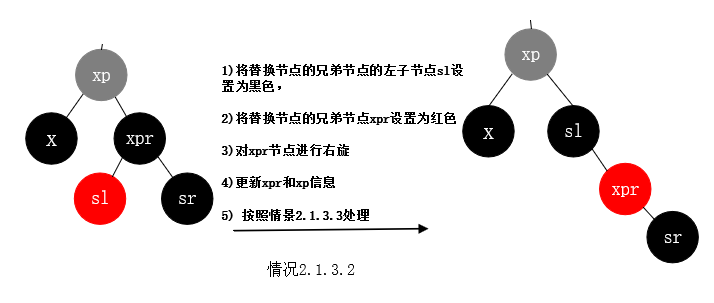
情况2.1.3.3: 删除节点为黑色, 替换节点是其父节点的左子树, 替换节点的兄弟节点存在且颜色为黑色, 替换节点的兄弟节点的右子节点是红色 左子节点任意颜色
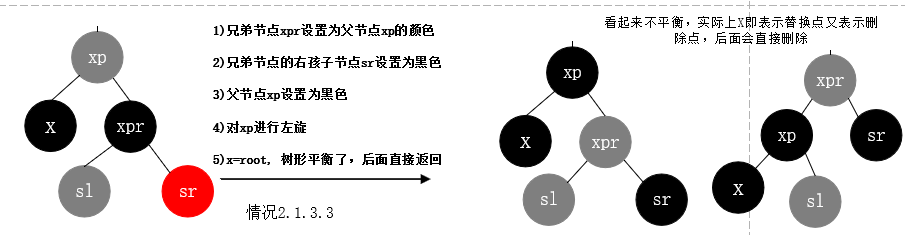
替换节点是父节点的右子树情况和上述左子树情况对称
情况2.2.1: 删除节点为黑色, 替换节点是黑色, 替换节点是其父节点的右子树, 替换节点的兄弟节点是红色。
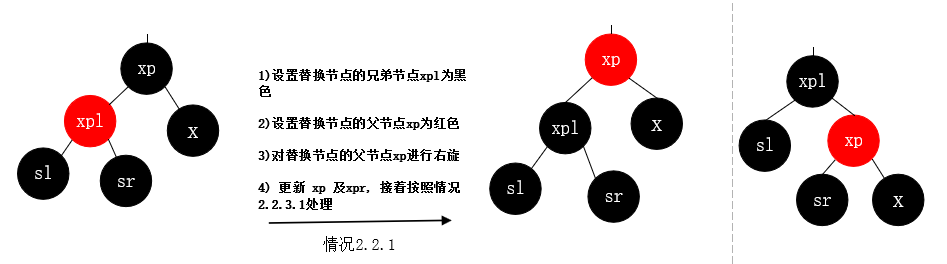
情况2.2.3.1: 删除节点为黑色, 替换节点是黑色, 替换节点是其父节点的右子树, 替换节点的兄弟节点是黑色, 替换节点的兄弟节点的子节点都为黑色。
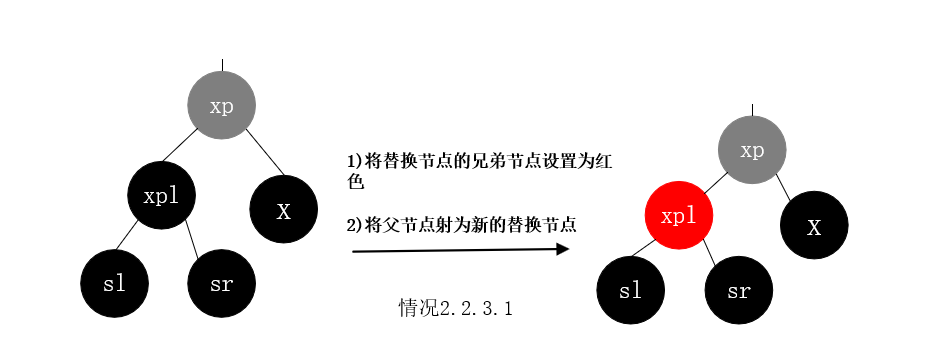
情况2.2.3.2: 删除节点为黑色, 替换节点是黑色, 替换节点是其父节点的右子树, 替换节点的兄弟节点是黑色,替换节点的兄弟节点的左节点为黑色 右节点为红色。
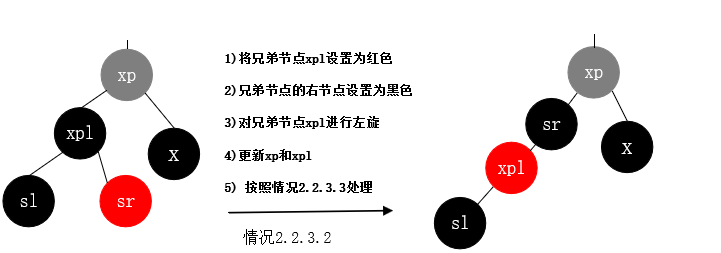
情况2.2.3.3: 删除节点为黑色, 替换节点是黑色, 替换节点是其父节点的右子树, 替换节点的兄弟节点是黑色,替换节点的兄弟节点的左子节点为红色右子节点任意颜色
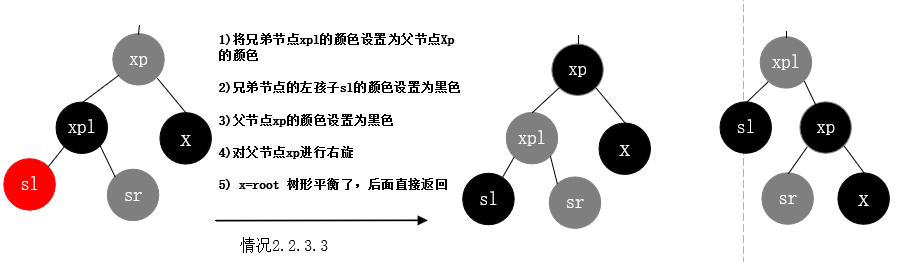
两个删除之后的调整案例
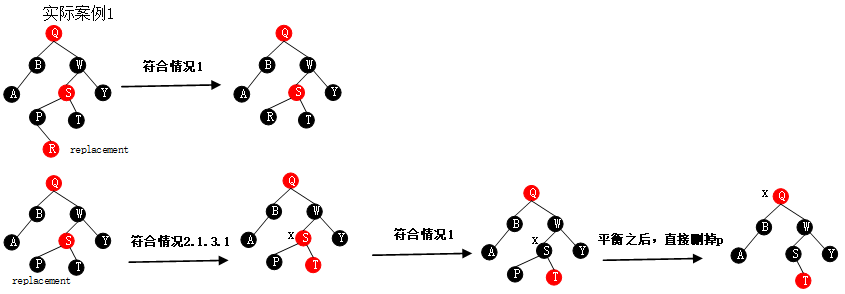
// 树形化方法分析, 此方法是TreeNode类中的方法, 它主要使用相应桶中的第一个元素来调用此方法,从而构造树形结构。普通节点链表中的每一个节点,插入到新构建的树形结构中包含两部。
第一步: 在树中找到插入位置,然后插入。 第二步:插入之后的平衡调整问题。
final void treeify(Node<K,V>[] tab) {
TreeNode<K,V> root = null;
for (TreeNode<K,V> x = this, next; x != null; x = next) {
next = (TreeNode<K,V>)x.next;
x.left = x.right = null;
if (root == null) {
x.parent = null;
x.red = false;
root = x;
}
else {
K k = x.key;
int h = x.hash;
Class<?> kc = null;
for (TreeNode<K,V> p = root;;) {
int dir, ph;
K pk = p.key;
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0)
// 默认的一种判断不可比较元素的大小的方法。也是为了保持记录的大小关系一致性
dir = tieBreakOrder(k, pk);
TreeNode<K,V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
x.parent = xp;
if (dir <= 0)
xp.left = x;
else
xp.right = x;
root = balanceInsertion(root, x);
break;
}
}
}
}
// 调整桶中第一个元素为树结构中的根节点
moveRootToFront(tab, root);
}
treeifyBin 方法对给定散列桶进行树形化,此方法首先设置双链表指针next和prev,接着调用treeify方法来树形化相应的桶中所有的元素。 treeifyBinf 方法在树形化之前会检查是否满足树形化条件(只检查第二个条件)
树形化条件有两个
第一对应桶中元素的个数超过阈值TREEIFY_THRESHOLD=8(在调用此方法时,已经满足此条件)
第二散列桶数组大小是否超过阈值 MIN_TREEIFY_CAPACITY, 没有超过阈值则进行扩容操作
/**
*hash 需要树形化的桶对应的散列码
*如果由于散列桶数组太小,不满足树形化条件的化,则进行rehash扩容操作
*/
final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
resize();
else if ((e = tab[index = (n - 1) & hash]) != null) {
TreeNode<K,V> hd = null, tl = null;
do { // 第一步设置双向链表, next和prev两个指针
TreeNode<K,V> p = replacementTreeNode(e, null);
if (tl == null)
hd = p;
else {
p.prev = tl;
tl.next = p;
}
tl = p;
} while ((e = e.next) != null);
// 第二步构建树结构, left和right两个指针
if ((tab[index] = hd) != null)
hd.treeify(tab);
}
}'''
部分参考下面文章
https://www.jianshu.com/p/e136ec79235c
https://www.jianshu.com/p/7b38abfc3298?utm_source=oschina-app 


