in front : 肯定不会写一些单纯的链表、栈、队列、二叉树啦 ,少年你别那么单纯。。。
学习该文章需要熟练掌握并理解的基础知识:链表、栈、队列、二叉树。。。
(最近在尝试费曼学习法哦)
下面进入今天的正题:
one:单调栈与单调队列
相信很多人一眼就明白了关键之处,没错就是单调。单调就是单调递增或单调递减,那么这种著名的单调思想有什么用呢?这种有序的思想在于及时排除不可能的(一定不是最优解的选项),保持策略集合(栈、队列)的高度有效性和秩序性。
简单来讲就是当数据进入(栈、队列)中是,若不满足单调性(单增或单减中选一个),则通过(pop)出栈、出队列来维持单调。很多小伙伴是不是想到函数单调呀 ,没错没有数学就没有算法。以我的理解就是用来处理一些最值问题。
运用单调栈
problem 1: 最大矩形面积
-
给定非负整数数组 ,数组中的数字用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱形图
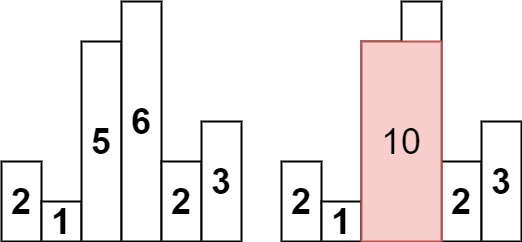
中,能够勾勒出来的矩形的最大面积。
- 输入: 输出:
- 6 10
- 2 1 5 6 2 3
- 解释:最大的矩形为图中红色区域,面积为 10
从左到右考虑,矩形一个一个进入。
首先,如果矩形的高度从左到右单调递增,那么答案是多少? 我们可以以每个矩形的高作为最终勾勒出的高,并向右延伸(递增是只能向右延伸的),在所有这样的勾勒出矩形面积更新找到最大值就是答案。
如果下一个矩形的高度比上一个小,那么该矩形利用左边的矩形(之前的)一起勾勒出新的矩形面积时,这块矩形的高度就不可能超过自己的高度。那么中间比该矩阵高的矩阵的高度信息就没有用处了。既然没有用处,为什么不把这些之前的比新入矩阵更高的矩阵全删了,把删了的矩阵宽度和加到新入矩阵的宽度中。这样我们维护的矩阵序列就成了一个单调递增的序列了,问题就变得简单了。
可以发现我们的操作都是在数组末尾进行的,所以这就是一个栈的结构啦。新入矩阵比栈顶矩阵高,直接进栈。新入矩阵比栈顶矩阵低,我们不断弹出比该矩阵高的矩阵,并用一个宽度为这些删去的矩阵宽度和加到新入矩阵的宽度中。最终变成了一个单调递增的序列,此时我们从栈顶向下考虑,不断增加width,乘以当前矩形的高度,更新ans)
add:(注意我们在新入矩阵时删除这些比新入矩形高的矩形也是一段单调递增的矩阵序列 这段序列也是要考虑的 在边删时 弹出时记录可能勾勒出的矩阵并更新答案)
可能讲的不是很清楚对于初学者来说。。。
但总结起来就时两点 首先要明白单调递增的矩阵序列是处理的 其次是怎么才能把序列变成单调递增序列 注意我们删去的把宽度加在新入矩阵上的矩阵序列也是递增序列 最后得到的也是递增矩阵序列。这就是单调栈咯 利用单调思想 (个人的一些thinking:其实感觉其中也有把问题拆成小问题的的思想 是设计算法与解决问题的重要思想 如dp、分治与递归等都是把大问题拆分成小问题。 )
#include<bits/stdc++.h> #define int long long using namespace std; const int N = 1e5 + 5; int a[N]; int s[N],w[N],idx; //s数组模拟栈 w数组记录栈里记录的矩阵的宽度 idx记录栈顶 signed main() { int n, ans = 0; scanf("%lld", &n); for (int i = 1; i <= n; i++) { scanf("%lld", &a[i]); } for (int i = 1; i <= n; i++) { if (a[i] > s[idx]) { //如果大于栈顶元素直接进栈 s[++idx] = a[i]; w[idx] = 1; } else { int width1 = 0;
//把比新入矩阵高的原有矩阵一个个出栈 此时不要忘记了这段比新入矩阵高的矩阵也是一段单调递增矩阵序列也是要考虑的
//用处理单调递增矩阵序列的方法 从后往前(从栈顶到下)一次勾勒出可能满足题意的矩形 不断更新ans while (s[idx] > a[i]) { width1 += w[idx]; ans = max(ans, width1 * s[idx]); idx--; } s[++idx] = a[i]; w[idx] = width1 + 1; //把之前删去的数组宽度加到新入矩形的宽度里 } } int width2 = 0; //此时再按照处理单调子序列的方法处理最终的递增矩形序列并更新答案即可 for (int i = idx; i >=1; i--) { width2 += w[i]; ans = max(ans, width2 * s[i]); } cout << ans; }
运用单调队列:
problem 2:最大子列和
输入一个长度为 n 的整数序列,从中找出一段长度不超过 m 的连续子序列,使得子序列中所有数的和最大。注意: 子序列的长度至少是1。
首先求连续子序列的和,我们的做法是把序列的前缀和先求出来,前缀和之差等于连续子序列之和。(这里有一定算法基础的应该很自然想得到,其实也是dp的思想)我们发现,当前缀和递减时,那么这样用后面减去前面就为负数了,这样肯定不是正确答案,所有,我们只需要维护出单调递增的前缀和序列就可以了,如果前缀和数组的某些数造成了递减,直接删去。
使用队列维护序列使其单调,就是单调队列,我们这里使用队列维护,队尾进,队头出。
1.判断队头的决策与 i (1<=i<=n)的距离是否超出m的范围,超出则出队。
2.更新ans。
3.删除队尾那些使其不递增的数
4.最后把i作为一个新的决策入队。
#include<bits/stdc++.h> using namespace std; const int N=3e5+10; int a[N]; int ans=-1<<31;//负无穷大 int q[N]; int t,h;//t是队尾,h是队头,用数组模拟队列 int main() { int n,m; cin>>n>>m; for(int i=1;i<=n;i++) { cin>>a[i]; a[i]+=a[i-1];//计算前缀和 } for(int i=1;i<=n;i++) {
//下面几步可以代几个数据进去理解一下。 if(q[h]<i-m) h++;//维护单调队列,队头。 ans=max(ans,a[i]-a[q[h]]); //更新ans while(h<=t&&a[q[t]]>=a[i]) t--;//维护单调队列,队尾。 q[++t]=i; //把i作为一个新的决策入队 } cout<<ans<<endl; }
由于每个元素至多入队一次,出队一次,所以时间复杂度为O(n)。它的思想也是在决策集合(队列)中及时排除一定不是最优解的选择(利用单调性)。
运用单调队列优化dp
引:单调栈和单调队列的本质都是借助单调性,及时排除不可能的决策,我们回想上一个单调队列的题目。ans=max{ a[i]-min( a[j] )}(i-m<=j<=i-1),有粗浅了解一些动态规划的同学已经知道,i就对应动态规划里的“状态”,j就对应动态规划里的“决策”,我们发现决策的范围(i-m<=j<=i-1),都和 i 线性相关,且前面的常数都一样,即范围的上下界变化都是一致的,单调队列非常适合优化这种问题,把不必要的决策优化掉。(把O(n*m)优化成O(n))
problem 3: 例题:2022 Jiangsu Collegiate Programming Contest Tutorial
C - Jump and Treasure (可直接点击)
可以得到状态转移方程,f [i] = max (f [j]) + a[i] i−j≤p,这是一个经典的单调队列优化 dp 的模型,利用单调队列(单调性)优化不必要的决策。
#include<bits/stdc++.h> #define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0); using namespace std; const int N = 1e6 + 10; int T, n, m, k; int va[N]; int dp[N]; //走到这个i点的最小花费,选择i点。 int anw[N]; int q[N], hh, tt; int solve(int x) { if (x > m) return -1; hh = 0, tt = -1; q[++tt] = 0; for (int i = x; i <= n; i += x) { while (hh <= tt && (q[hh] + m) < i) ++hh; //维护单调队列,队头。 dp[i] = dp[q[hh]] + va[i]; //这里先更新,你才能把dp[i]放进去比较 //转移 while (hh <= tt && dp[q[tt]] <= dp[i]) --tt; //维护单调队列,队尾。 q[++tt] = i;//进队列,从队列尾进。 } while (hh <= tt && q[hh] + m < n + 1) ++hh;//队列头的位置 return dp[q[hh]]; } signed main() { IOS; cin >> n >> k >> m; for (int i = 1; i <= n; i++) cin >> va[i]; for (int i = 1; i <= n; i++) anw[i] = solve(i); while (k--) { int x; cin >> x; if (anw[x] == -1) cout << "Noob\n"; else cout << anw[x] << "\n"; } }
two:字符串hash
字符串hash把一个字符串映射成了一个非负整数(没错就是函数的映射概念)。取一个值p,把字符串看成p进制数,分配一个大于0的数值,代表每种字符。例:S="abc",a=1,b=2,c=3......(以此类推),H(s)=1*p2+2*p+3。字符串hash就是一种这么简单容易理解的数据结构。
problem 4:139. 回文子串的最大长度 - AcWing题库
#include<bits/stdc++.h> using namespace std; typedef unsigned long long ULL; //直接用unsigned int long long 类型存储这个hash值 //在计算中不处理算数溢出问题,产生溢出时相当于自动对2^64取模 //避免了低效的取模运算 const int N = 2000010, P = 131; ULL hl[N], hr[N], p[N]; char str[N]; ULL get(ULL h[], int l, int r) { return h[r] - h[l - 1] * p[r - l + 1]; } signed main() { int T = 1, n; while (cin >> str + 1 && strcmp(str + 1, "END")) { n = strlen(str + 1); for (int i = n * 2; i; i -= 2) { str[i] = str[i / 2]; str[i - 1] = 'a' + 26; } p[0] = 1, n *= 2; for (int i = 1, j = n; i <= n; i++, j--) { hl[i] = hl[i - 1] * P + str[i];// 正序哈希 hr[i] = hr[i - 1] * P + str[j];// 逆序哈希 p[i] = p[i - 1] * P; } int res = 0; for (int i = 1; i <= n; i++) { int l = 0, r = min(i - 1, n - i); while (l < r) //二分寻半径 { int mid = l + r + 1 >> 1; if (get(hl, i - mid, i - 1) != get(hr, n - (mid + i) + 1, n - (i + 1) + 1)) r = mid - 1; else l = mid; } if (str[i - l] <= 'z') res = max(res, l + 1); else res = max(res, l); } printf("Case %d: %d\n", T++, res); } }
(努力更新中)



