机器学习十讲第三讲
1. 数学知识回顾:点到平面距离、梯度下降法、最大似然估计
点到平面的距离:
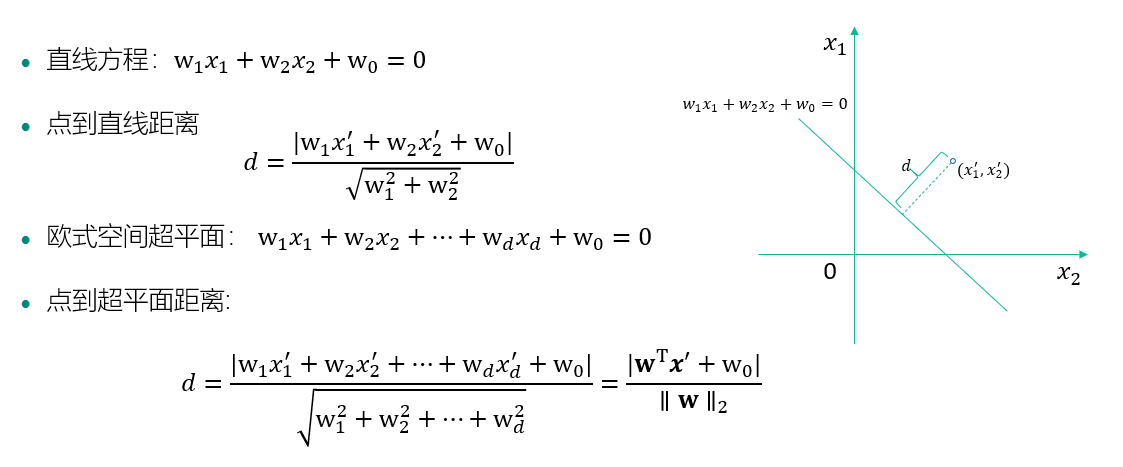
梯度下降法:

随机梯度下降法
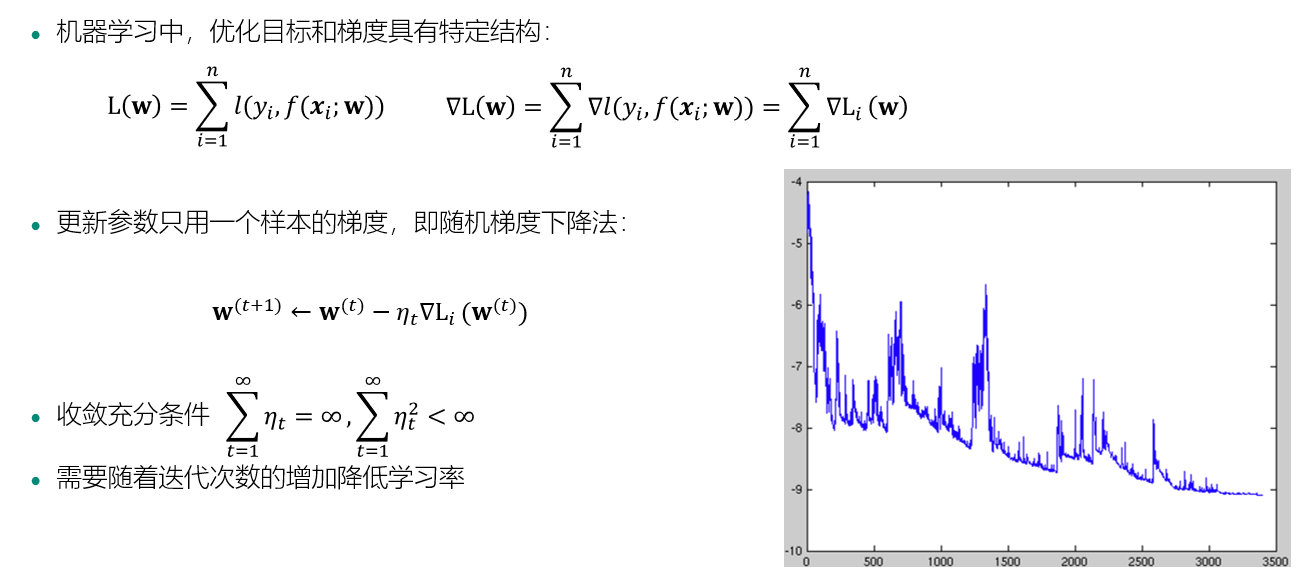
最大似然估计:


什么是分类:

如何做分类:

感知机、支持向量机和逻辑回归

训练集的矩阵表示
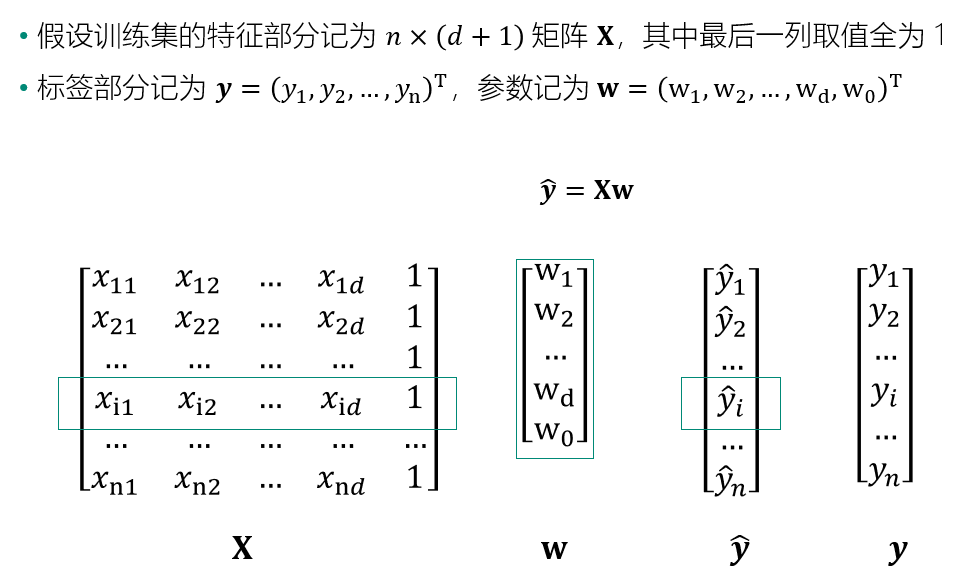
2. 感知机

感知机的优化目标
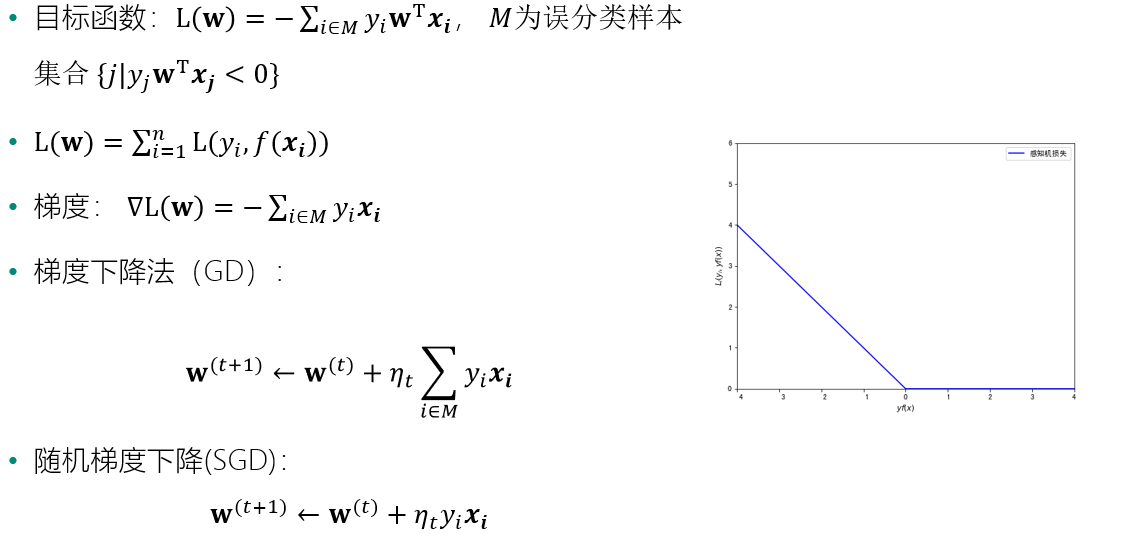
感知机算法:
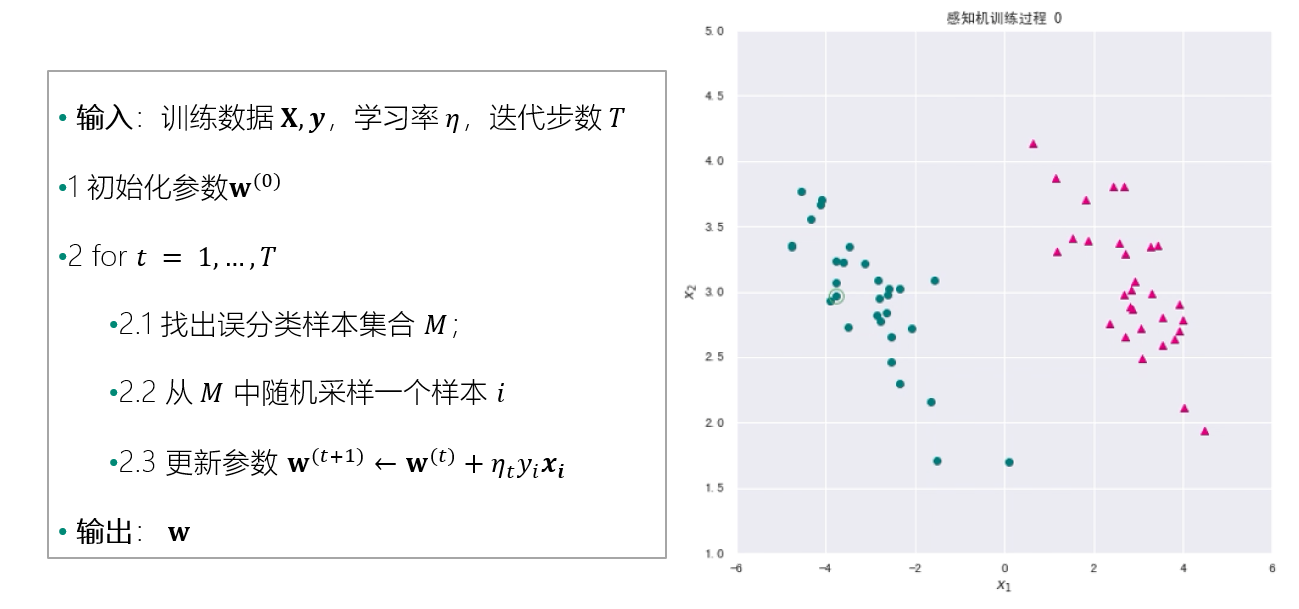
3. 支持向量机
间隔最大化

样本损失函数

优化目标

非线性:核技巧
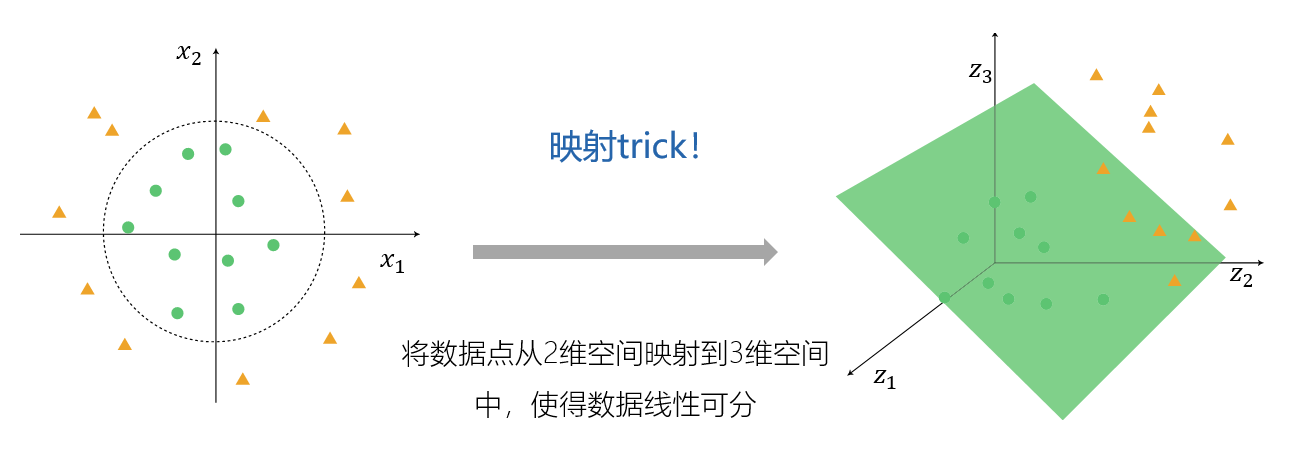
4. 逻辑回归
赋予样本概率解释

似然函数和负对数似然函数

损失函数
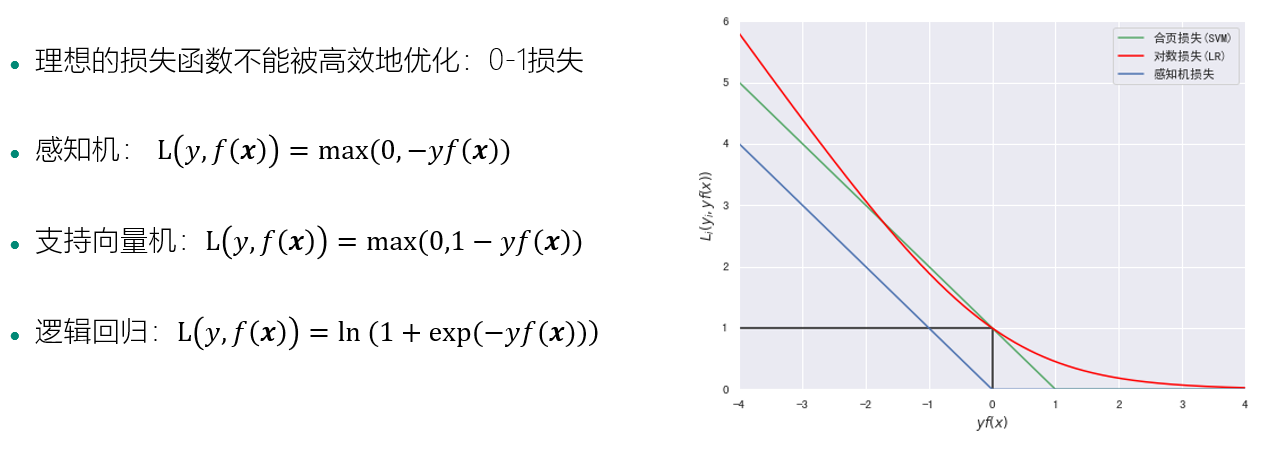
5. 分类模型估计和Sklearn 分类模块
分类问题的评价指标

Sklearn 分类模块介绍
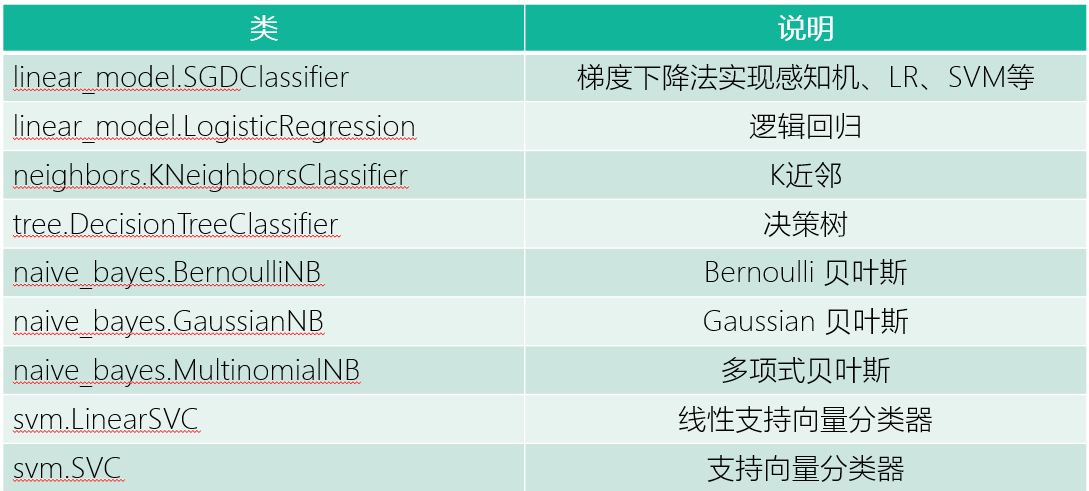

6. 案例:使用感知机、逻辑回归和支持向量机进行中文新闻分类
1 生成数据集
首先使用 sklearn 中的 datasets 模块生成一个随机的二分类数据集。
from sklearn import datasets random_samples = datasets.make_classification(n_samples=60, #样本数量 n_classes=2, #类别数量 n_features=2, #特征数量 n_informative=2,#有信息特征数量 n_redundant=0, #冗余特征数量 n_repeated=0, # 重复特征数量 n_clusters_per_class=1, #每一类的簇数 flip_y=0, # 样本标签随机分配的比例 class_sep=3,#不同类别样本的分散程度 random_state=203)
为了便于后续处理,我们将生成的数据封装到 Pandas 的 DataFrame 中。 数据集数据包含两个特征,特征名为 x1 和 x2,标签值存放在 label 中。为了后续处理方便,我们给数据集添加一个取值全为 1 的列 ones。
import pandas as pd data = pd.DataFrame(data=random_samples[0],columns=["x1","x2"]) data["label"] = random_samples[1] data["ones"] = 1 #添加一个取值全为 1 的列 `ones` data.head()
在本案例即将实现的算法中,我们假设标签取值为 1 或 -1,观察上表 label 列取值可见,默认的取值为 0 或 -1 。应用 map 方法,我们将 label 列的取值映射为 1 和 -1 。
data["label"] = data["label"].map({0:-1,1:1}) # 将 y 的取值替换成 1 和 -1
为了直观地了解数据,我们将数据集用散点图绘制出来。matplotlib.pyplot 模块的 scatter 函数可以绘制散点图,它的主要参数为横轴数据 x ,纵轴数据 y,点的颜色 c ,点的形状等 marker 。
数据集中正样本和负样本需要进行区分,我们首先将他们进行分离。
data_pos = data[data["label"]==1] # 筛选出正样本 data_neg = data[data["label"]==-1] # 筛选出负样本
将绘图框大小设置成 (8,8),然后将正样本画成洋红色(c="#E4007F")的三角形(marker="^"),将负样本画成深绿色(c="#007979")的圆形(marker="^")。
import matplotlib.pyplot as plt %matplotlib inline plt.rcParams['axes.unicode_minus'] = False plt.figure(figsize=(8, 8)) #设置图片尺寸 plt.scatter(data_pos["x1"],data_pos["x2"],c="#E4007F",marker="^") # 类别为1的数据绘制成洋红色 plt.scatter(data_neg["x1"],data_neg["x2"],c="#007979",marker="o") # 类别为-1的数据绘制成深绿色 plt.xlabel("$x_1$") #设置横轴标签 plt.ylabel("$x_2$") #设置纵轴标签 plt.xlim(-6,6) #设置横轴显示范围 plt.ylim(1,5) #设置纵轴显示范围 plt.show()
假设我们学习到的决策直线方程为 w1x1+w2x2+w0=0w1x1+w2x2+w0=0,即直线上的点满足以下关系 x2=−w1w2x1−w0w2x2=−w1w2x1−w0w2。所以一旦得到直线方程,我们首先生成横轴数据 x1,然后根据上述公式计算对应的纵轴取值 x2 ,最后利用 matplotlib 的 plot 函数就可以将直线绘制出来。
import numpy as np w = [1,1,-4] x1 = np.linspace(-6, 6, 50) x2 = - (w[0]/w[1])*x1 - w[2]/w[1]
plt.figure(figsize=(8, 8)) #设置图片尺寸
plt.scatter(data_pos["x1"],data_pos["x2"],c="#E4007F",marker="^") # 类别为1的数据绘制成洋红色
plt.scatter(data_neg["x1"],data_neg["x2"],c="#007979",marker="o") # 类别为-1的数据绘制成深绿色
plt.plot(x1,x2,c="gray") # 画出分类直线
plt.xlabel("$x_1$") #设置横轴标签
plt.ylabel("$x_2$") #设置纵轴标签
plt.xlim(-6,6) #设置横轴显示范围
plt.ylim(1,5) #设置纵轴显示范围
plt.show()
感知机的损失函数为L(w)=−∑xi∈Myi(wTxi)L(w)=−∑xi∈Myi(wTxi),其中MM为误分类样本集合。训练姐中没有误分类样本时,损失函数L(w)L(w)为0,误分类样本数量越少,误分类样本与超平面的距离就越近,因此损失函数也就越小。
可由损失函数得出梯度如下:
随机选取一个误分类样本(xi,yi)(xi,yi),对参数ww的更新方法如下:
其中ηη为学习率,0<η≤10<η≤1,这样通过迭代就可以使损失函数减小,直到损失函数为0。
使用随机梯度下降法的感知机算法为:

下面用一个 perception 函数实现上述算法。为了深入观察算法运行过程,我们保留了每一轮迭代的参数 ww,并对每一轮迭代中随机选取的样本也进行了记录。所以,perception 函数返回三个取值: 最终学习到的参数 w, 每轮迭代的参数 W, 每轮迭代随机选取的样本 mis_samples 。
def perception(X,y,learning_rate,max_iter=1000): w = pd.Series(data=np.zeros_like(X.iloc[0]),index=X.columns) # 初始化参数 w0 W = [w] # 定义一个列表存放每次迭代的参数 mis_samples = [] # 存放每次误分类的样本 for t in range(max_iter): # 2.1 寻找误分类集合 M m = (X.dot(w))*y #yw^Tx < 0 的样本为误分类样本 X_m = X[m <= 0] # 误分类样本的特征数据 y_m = y[m <= 0] # 误分类样本的标签数据 if(len(X_m) > 0): # 如果有误分类样本,则更新参数;如果不再有误分类样本,则训练完毕。 # 2.2 从 M 中随机选取一个样本 i i = np.random.randint(len(X_m)) mis_samples.append(X_m.iloc[i,:]) # 2.3 更新参数 w w = w + learning_rate * y_m.iloc[i]*X_m.iloc[i,:] W.append(w) else: break mis_samples.append(pd.Series(data=np.zeros_like(X.iloc[0]),index=X.columns)) return w,W,mis_samples
现在,让我们使用上一节生成的数据集来测试一下上述感知机算法吧。
w_percept,W,mis_samples = perception(data[["x1","x2","ones"]], data["label"],1,max_iter=1000)
首先,将学习到的感知机的决策直线可视化,观察分类效果。
x1 = np.linspace(-6, 6, 50)
x2 = - (w_percept[0]/w_percept[1])*x1 - w_percept[2]/w_percept[1]
plt.figure(figsize=(8, 8)) #设置图片尺寸 plt.scatter(data_pos["x1"],data_pos["x2"],c="#E4007F",marker="^") # 类别为1的数据绘制成洋红色 plt.scatter(data_neg["x1"],data_neg["x2"],c="#007979",marker="o") # 类别为-1的数据绘制成深绿色 plt.plot(x1,x2,c="gray") # 画出分类直线 plt.xlabel("$x_1$") #设置横轴标签 plt.ylabel("$x_2$") #设置纵轴标签 plt.title('手动实现的感知机模型') plt.xlim(-6,6) #设置横轴显示范围 plt.ylim(1,5) #设置纵轴显示范围 plt.show()
由于已经记录了每一轮迭代中参数和选取的样本,我们将感知机的学习过程动态展示出来。我们可以借助 matplotlib.animation 动画模块来实现。在我们的动画中,样本数据保持不变,每个图片中变化的是决策实现和随机选取的样本。下面的 init_draw 函数是动画最开始时绘制的内容,只包含数据。update_draw 则是每次更新的内容,我们根据参数将决策直线进行更新,将选取的样本用圆圈进行标记。
#plt.rcParams['figure.dpi'] = 120 #分辨率 fig, ax = plt.subplots(figsize=(8, 8)) line, = ax.plot([],[],c="gray") ## 决策直线对象 dot, = ax.plot([],[],"go", linewidth=2, markersize=12,markerfacecolor='none') ## 误分类样本对象 def init_draw(): # 展现样本数据 ax.set_title("感知机训练过程") ax.scatter(data_pos["x1"],data_pos["x2"],c="#E4007F",marker="^") # 类别为1的数据绘制成洋红色 ax.scatter(data_neg["x1"],data_neg["x2"],c="#007979",marker="o") # 类别为-1的数据绘制成深绿色 plt.xlabel("$x_1$") plt.ylabel("$x_2$") plt.xlim(-6,6) plt.ylim(1,5) def update_draw(i): # 实现动画中每一帧的绘制函数,i为第几帧 ax.set_title("感知机训练过程 "+ str(i)) w = W[i] #获取当前迭代的参数 x1 = np.linspace(-6, 6, 50) x2 = - (w[0]/w[1])*x1 - w[2]/w[1] line.set_data(x1,x2) #更新决策直线绘制 dot.set_data(mis_samples[i]["x1"],mis_samples[i]["x2"]) # 更新选取的样本标记 plt.close() #演示决策面动态变化 import matplotlib.animation as animation from IPython.display import HTML animator = animation.FuncAnimation(fig, update_draw, frames= range(0,len(W)), init_func=init_draw,interval=2000) HTML(animator.to_jshtml())
/explorer/pyenv/jupyter-py36/lib/python3.6/site-packages/ipykernel_launcher.py:19: RuntimeWarning: invalid value encountered in double_scalars
接下来,我们将分别使用两种不同的优化方法进行逻辑回归算法的实现。已知逻辑回归的目标函数为负对数似然函数 NLL(w)=∑ni=1ln(1+e−yiwTxi)NLL(w)=∑i=1nln(1+e−yiwTxi),梯度为 ∇NLL(w)=−∑ni=1yixi1+eyiwTxi∇NLL(w)=−∑i=1nyixi1+eyiwTxi ,则:
-
使用梯度下降法求解的迭代公式为:
w(t+1)←w(t)+ηt∑i=1nyixi1+eyiw(t)Txiw(t+1)←w(t)+ηt∑i=1nyixi1+eyiw(t)Txi -
使用随机梯度下降法的迭代求解公式为:
w(t+1)←w(t)+ηtyixi1+eyiw(t)Txiw(t+1)←w(t)+ηtyixi1+eyiw(t)Txi
首先,我们来一起实现使用梯度下降求解的逻辑回归算法:
import numpy as np # 定义梯度下降法求解的迭代公式 def logistic_regression(X,y,learning_rate,max_iter=1000): # 初始化w w = np.zeros(X.shape[1]) for t in range(max_iter): # 计算yX yx = y.values.reshape((len(y),1)) * X # 计算1 + e^(yXW) logywx = (1 + np.power(np.e,X.dot(w)*y)).values.reshape(len(y),1) w_grad = np.divide(yx,logywx).sum() # 迭代w w = w + learning_rate * w_grad return w
我们将数据及标签带入上面定义的函数,学习率设为 0.5 ,迭代次数为1000次,输出训练好的参数,并将分类结果进行可视化。
# 输出训练好的参数 w = logistic_regression(data[["x1","x2","ones"]], data["label"],0.5,max_iter=1000) print(w) # 可视化分类结果 x1 = np.linspace(-6, 6, 50) x2 = - (w[0]/w[1])*x1 - w[2]/w[1] plt.figure(figsize=(8, 8)) plt.scatter(data_pos["x1"],data_pos["x2"],c="#E4007F",marker="^") # 类别为1的数据绘制成洋红色 plt.scatter(data_neg["x1"],data_neg["x2"],c="#007979",marker="o") # 类别为-1的数据绘制成深绿色 plt.plot(x1,x2,c="gray") plt.xlabel("$x_1$") plt.ylabel("$x_2$") plt.xlim(-6,6) plt.ylim(1,5) plt.show()
x1 43.891185 x2 -4.351429 ones -3.605057 dtype: float64
接下来,我们一起实现使用随机梯度下降法的逻辑回归算法,随机梯度下降法的迭代求解公式为:
# 定义随机梯度下降法求解的迭代公式 def logistic_regression_sgd(X,y, learning_rate, max_iter=1000): # 初始化w w = np.zeros(X.shape[1]) for t in range(max_iter): # 随机选择一个样本 i = np.random.randint(len(X)) # 计算yx yixi = y[i] * X.values[i] # 计算1 + e^(yxW) logyiwxi = 1 + np.power(np.e, w.T.dot(X.values[i])*y[i]) w_grad = yixi / logyiwxi # 迭代w w = w + learning_rate * w_grad return w
我们将学习率设为 0.5,迭代次数为1000次,并输出训练好的参数,将分类结果可视化。
# 输出训练好的参数 w = logistic_regression_sgd(data[["x1","x2","ones"]], data["label"],0.5,max_iter=1000) print(w) # 可视化分类结果 x1 = np.linspace(-6, 6, 50) x2 = - (w[0]/w[1])*x1 - w[2]/w[1] plt.figure(figsize=(8, 8)) plt.scatter(data_pos["x1"],data_pos["x2"],c="#E4007F",marker="^") # 类别为1的数据绘制成洋红色 plt.scatter(data_neg["x1"],data_neg["x2"],c="#007979",marker="o") # 类别为-1的数据绘制成深绿色 plt.plot(x1,x2,c="gray") plt.xlabel("$x_1$") plt.ylabel("$x_2$") plt.xlim(-6,6) plt.ylim(1,5) plt.show()



