图总结

一.思维导图

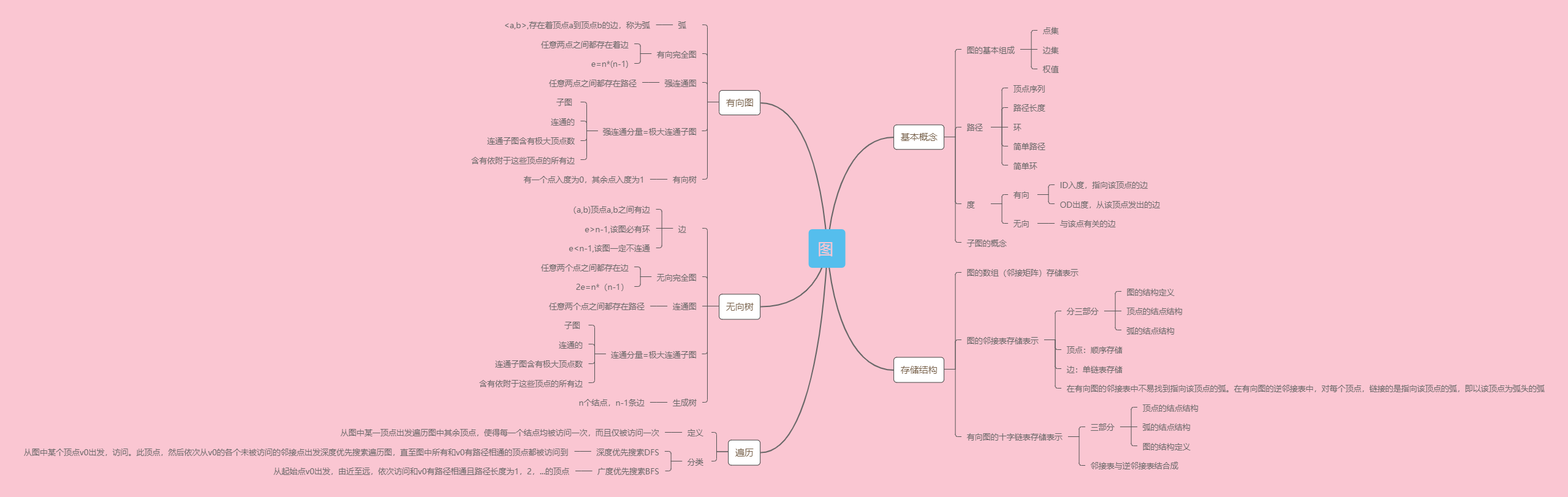
二.图的重要概念
1.图的基本概念和术语
（1）图之间的关系可以是任意的，任意两个数据元素之间都可能相关。
(2) 顶点：数据元素。
(3) 边or弧：从一个顶点到另一个顶点的路径。<V,M>表示弧，（V,M)表示边，V是弧尾，W是弧头，此时为有向图，否则为无向图。
(4) 对于无向图，边的取值范围是0到1/2n(n-1)。有1/2n(n-1)条边的无向图为完全图。对于有向图，边的取值范围0到n(n-1),n*(n-1)称作有向完全图。
2.图的存储结构
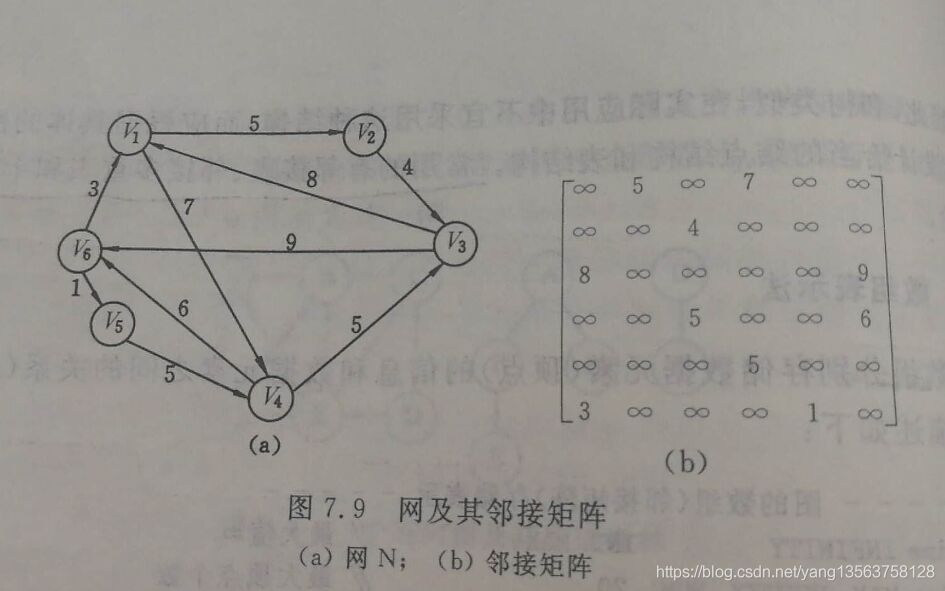
常见的图的存储结构分为：邻接表，邻接多重表，十字链表。能方便使用的是邻接表。

3.图的遍历
从图的某一顶点出发访问图的其他顶点，且只访问一次，叫图的遍历。
(1) 图的深度优先遍历（DFS):它从图中某个顶点v出发，访问此顶点，然后从v未被访问的邻接点出发深度优先遍历图，直至图中所有和v有路径相同的顶点都被访问
到。

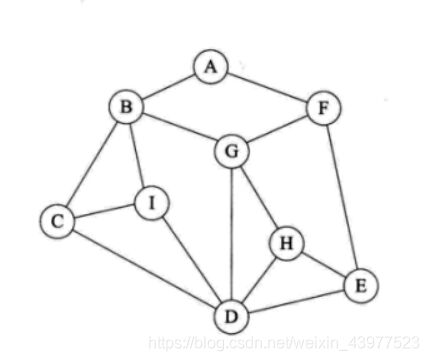
首先我们从A点出发，我们给自己定一个原则，在没有碰到重复顶点的情况下，始终向右手边走。于是我们依据右手通行原则，走到了B顶点，然后再走到了C顶 
点，继续走又走到了D顶点，接着又走到了E顶点，接着又走到F顶点，在F点我们发现右手边是A点，是已经访问过的点，于是我们走到了G顶点，在G点发现B、D两 
点都已经访问过了，于是走到H点，到了H点后发现没有没被访问过的点，退回到G点，G点也没有，所以退回F点，F点一样没有，所以退回到E点，E一样，再退回 
到D点，到了D点还有I点没有被访问过,走到I点，到了I点发现没有没被访问过的点，退回到D点，D点也没有，退回到C点，C点也没有，退回到B点，B点也没有， 
退回到A点。A点也没有。此时遍历过程结束。

(2) 图的广度优先遍历（BFS)

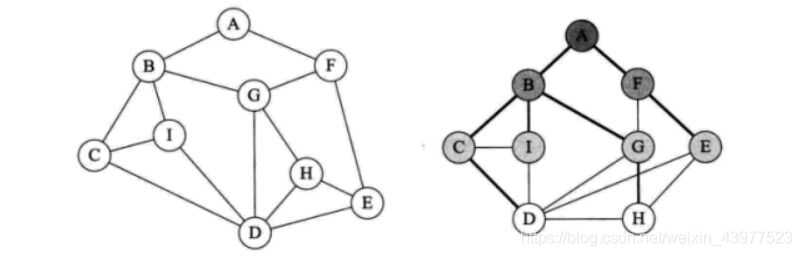
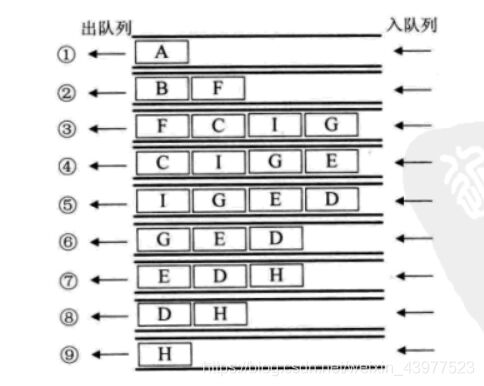
首先，先将A点入队，A点被访问过了，队列不能为空，将A出队，然后将A未访问的邻接点B,F入队。此时队还不为空，将B出队，然后将B的未访问的邻接点
C,I,G入队。队仍然不为空，将F出队，再将F的未访问邻接点E入队。队依然不为空，将C出队，然后把C的未访问的邻接点D入队。队依然不为空，将I出队，I没
有未被访问的邻接点。此时队仍然不为空，将G出队，再将G的未访问邻接点H入队。然后队不为空E出队，E没有未被访问的邻接点。然后队依然不为空D出队，D
没有未被访问的邻接点。然后队不为空H出队，H没有未被访问的邻接点。最后队为空。结束。
具体过程如下图：

4.最小生成树
(1) 最小生成树不是唯一的，最小生成树的树形不唯一，但最小生成树的边的权值和是唯一的。
(2) 图的各边权值互不相等，则图的最小生成树唯一。
(3) 最小生成树的边数=n-1。
普利姆（prime):第一种：先将一个起点加入最小生成树，之后不断寻找与最小生成树相连的边权最小的边能通向的点，并将其加入最小生成树，直至所有顶点都在最小生成树中。

           第二种：将一个图的顶点分为两部分，一部分是最小生成树中的结点（A集合），另一部分是未处理的结点（B集合）。
                  首先选择一个结点，将这个结点加入A中，然后，对集合A中的顶点遍历，找出A中顶点关联的边权值最小的那个（设为v），将此顶点从B中 
                  删除，加入集合A中。
                  递归重复步骤2，直到B集合中的结点为空，结束此过程。
                  A集合中的结点就是由Prime算法得到的最小生成树的结点，依照步骤2的结点连接这些顶点，得到的就是这个图的最小生成树。

克鲁斯卡尔(kluskal):在剩下的所有未选取的边中，找最小边，如果和已选取的边构成回路，则放弃，选取次小边。
三.疑难问题总结
对图的广度优先遍历还不是很理解。