树,二叉树，查找算法总结

1.思维导图

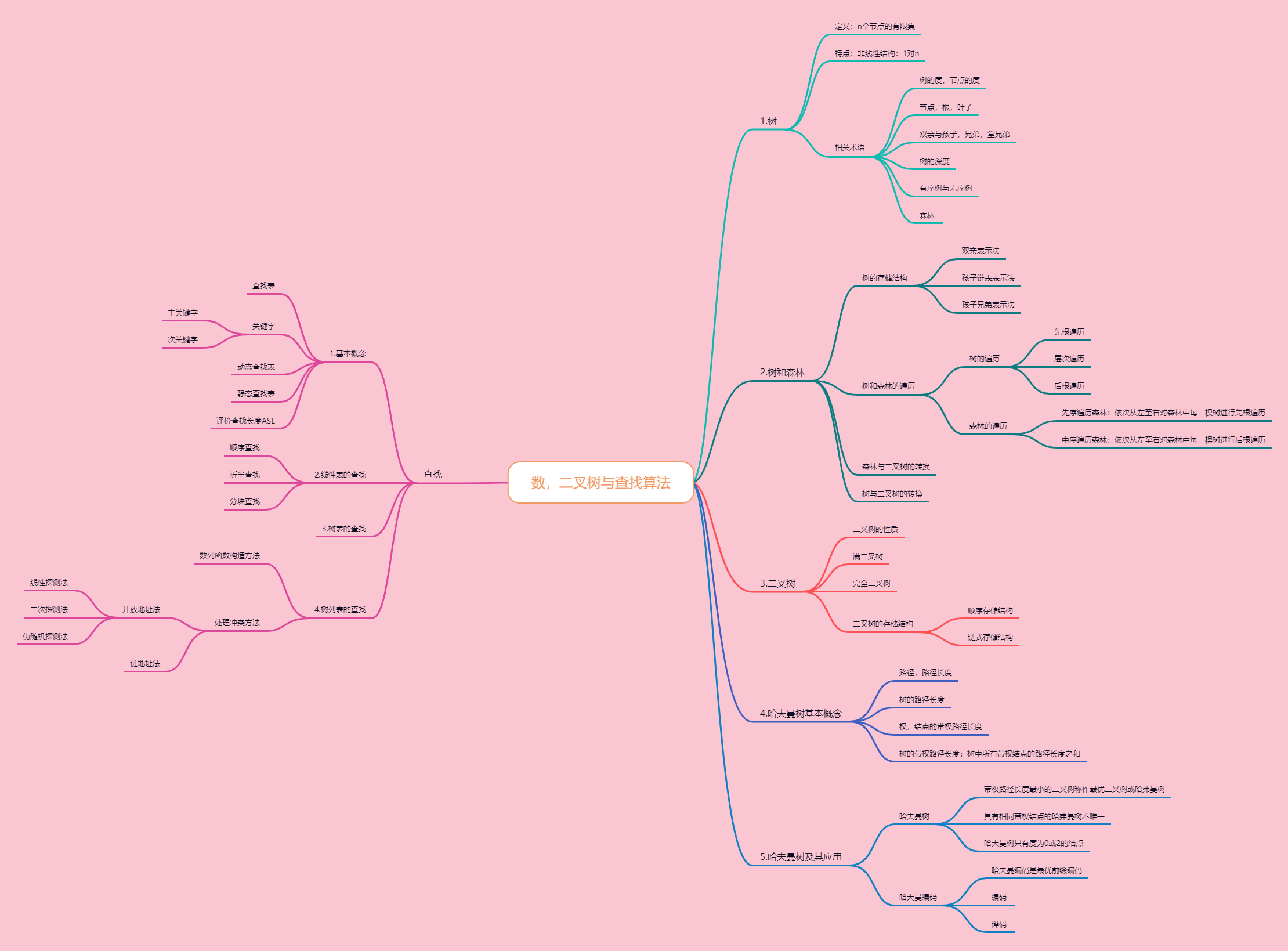
2.树，二叉树的重要概念
（1）树包含的基本概念
结点：树的数据元素
结点的度：结点挂接的子树数
结点的层次：从根到该节点的层数（根结点算第一层）
终端结点：度为0的结点，即叶子
分支结点：度不为0的结点
树的度：所有结点中度的最大值
树的深度：所有结点中最大的层数
双亲：上层的那个结点
孩子：下层结点的子树的根
兄弟：同一双亲的同层结点
堂兄弟：双亲位于同一层的结点
祖先：从根到该结点所经分支的所有结点
子孙：该结点下层子树中任一结点
（2）二叉树（二叉树的结构最简单，规律性最强；所有树均能转为唯一对应的二叉树，不失一般性。二叉树不是树。）
特殊二叉树：1.满二叉树：除叶子结点外的结点度均为2
2.完全二叉树：只有最后一层叶子不满且全部集中在左边
关系：满二叉树必为完全二叉树，完全二叉树不一定是满二叉树
（3）二叉树的性质
1.在二叉树的第i层上至多有2^(i-1)个
2.深度为k的二叉树至多有2^k-1个结点，至少有k个结点
3.叶子结点数=度为2的结点数+1
4.对完全二叉树，若从上至下，从左至右编码，则编号为i的结点，其左孩子的编号一定为2i,其右孩子的编号一定为2i+1,其双亲的编号一定为i/2
(4)二叉树的遍历

3.哈夫曼树：最优二叉树，即带权路径长度最短的二叉树。
哈夫曼树的构造过程：1.对结点权值升序排序，从结点序列中选择两个权值最小的结点，小的放在左边，大的放在右边。创建新的结点，如选择1，2实数作为结点，
则创建的结点的权为3。
2.从序列中删除上一步选择的两个结点，再选一个最小的，将新建的结点加入序列。重复执行以上两步，最终节点序列中剩余的一个节点即为
最终的根结点。
3.哈夫曼编码：在每个路径上都添上0或1，左0右1。从根结点数到对应的叶子结点，路径上的值拼接起来就是叶子结点字母的应该的编码。1

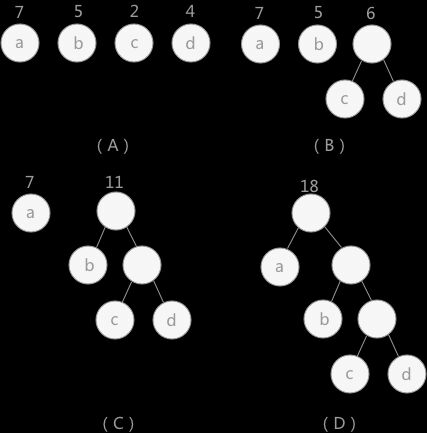
如上图所示，（A)给定了四个结点a,b,c,d,权值分别为7，5，2，4；第一步如(B)所示，找出现有权值中最小的两个2，4，相应的结点c,d构
建一个新的二叉树，树根的权值为2+4=6，同时将原有权值中的2，4删掉，将新的权值6加入，进入（C)，重复之前的步骤。直到（D)中，所有
结点构成一个全新的二叉树，即为哈夫曼树。