Codeforces 706D Trie树/multiset
Author has gone out of the stories about Vasiliy, so here is just a formal task description.
You are given q queries and a multiset A, initially containing only integer 0. There are three types of queries:
- "+ x" — add integer x to multiset A.
- "- x" — erase one occurrence of integer x from multiset A. It's guaranteed that at least one x is present in the multiset A before this query.
- "? x" — you are given integer x and need to compute the value
![]() , i.e. the maximum value of bitwise exclusive OR (also know as XOR) of integer x and some integer y from the multiset A.
, i.e. the maximum value of bitwise exclusive OR (also know as XOR) of integer x and some integer y from the multiset A.
Multiset is a set, where equal elements are allowed.
The first line of the input contains a single integer q (1 ≤ q ≤ 200 000) — the number of queries Vasiliy has to perform.
Each of the following q lines of the input contains one of three characters '+', '-' or '?' and an integer xi (1 ≤ xi ≤ 109). It's guaranteed that there is at least one query of the third type.
Note, that the integer 0 will always be present in the set A.
For each query of the type '?' print one integer — the maximum value of bitwise exclusive OR (XOR) of integer xi and some integer from the multiset A.
10
+ 8
+ 9
+ 11
+ 6
+ 1
? 3
- 8
? 3
? 8
? 11
11
10
14
13
After first five operations multiset A contains integers 0, 8, 9, 11, 6 and 1.
The answer for the sixth query is integer 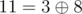 — maximum among integers
— maximum among integers 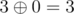 ,
, 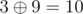 ,
, 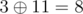 ,
, 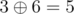 and
and 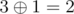 .
.
题意:
+表示吧这个数加到集合中,-表示把这个数从集合中减去一次,?表示集合里面的一个y使的x^y最大;
分析:
Trie树。
#include<bits/stdc++.h> using namespace std; const int N=1e7+9; int a[N][2],cal[N]; int tot; void add(int x,int y) //插入或删除一个元素 { int cur=0; for(int i=31;i>=0;i--){ int t=(x>>i)&1; if(!a[cur][t])a[cur][t]=tot++; cur=a[cur][t]; cal[cur]+=y; } } int query(int x) { int cur=0,ans=0; for(int i=31;i>=0;i--){ int t=(x>>i)&1; if(cal[a[cur][t^1]]){ ans+=(1<<i); cur=a[cur][t^1]; } else cur=a[cur][t]; } return ans; } int main() { int n,x; char op; tot=1; add(0,1); scanf("%d",&n); for(int i=0;i<n;i++){ cin>>op>>x; if(op=='+'){ add(x,1); } else if(op=='-'){ add(x,-1); } else{ printf("%d\n",query(x)); } } return 0; }
或者可以直接用multiset模拟:
#include<bits/stdc++.h> using namespace std; const int N=1e7+9; int main() { int n,x; char op; multiset<int>s; s.insert(0); scanf("%d",&n); for(int i=0;i<n;i++){ cin>>op>>x; if(op=='+'){ s.insert(x); } else if(op=='-'){ s.erase(s.find(x)); } else{ int ans=0; for(int i=31;i>=0;i--){ ans|=(~x&(1<<i)); multiset<int>::iterator it=s.lower_bound(ans); if(it==s.end()||*it>=ans+(1<<i)){ // cout<<ans<<endl; ans^=1<<i; } } printf("%d\n",x^ans); } } return 0; }


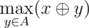 , i.e. the maximum value of bitwise exclusive OR (also know as XOR) of integer
, i.e. the maximum value of bitwise exclusive OR (also know as XOR) of integer 
 浙公网安备 33010602011771号
浙公网安备 33010602011771号