Codeforces 685B 树形dp

题意：给出有n个点的树，有q次询问某个点的重心是什么？

Input

The first line of the input contains two integers n and q (2 ≤ n ≤ 300 000, 1 ≤ q ≤ 300 000) — the size of the initial tree and the number of queries respectively.

The second line contains n - 1 integer p₂, p₃, ..., p_n (1 ≤ p_i ≤ n) — the indices of the parents of the nodes from 2 to n. Node 1 is a root of the tree. It's guaranteed that p_i define a correct tree.

Each of the following q lines contain a single integer v_i (1 ≤ v_i ≤ n) — the index of the node, that define the subtree, for which we want to find a centroid.

Output

For each query print the index of a centroid of the corresponding subtree. If there are many suitable nodes, print any of them. It's guaranteed, that each subtree has at least one centroid.

Example

Input

7 4
1 1 3 3 5 3
1
2
3
5

Output

3
2
3
6

Note

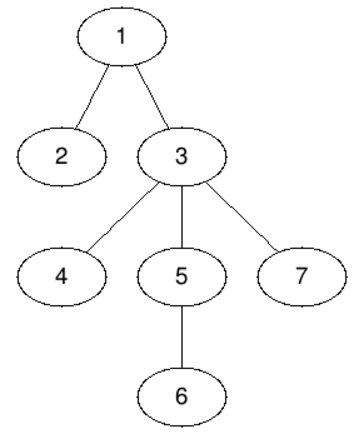
The first query asks for a centroid of the whole tree — this is node 3. If we delete node 3 the tree will split in four components, two of size 1 and two of size 2.

The subtree of the second node consists of this node only, so the answer is 2.

Node 3 is centroid of its own subtree.

The centroids of the subtree of the node 5 are nodes 5 and 6 — both answers are considered correct.

分析：

粘一下别人的题解：

先算出每个子树的节点个数，然后找里面最大的一棵子树，重心必然在这棵子树上（很明显的，因为重心是删除它之后，剩下的子树里面节点最大的最小，所以重心应该是在最大的子树里面），然后必然是在最大的子树的重心的上面，这也是显然的，所以可以直接从最大的子树的重心往上，直到找到第一个点满足num[res[u]]≥num[u]−num[res[u]]就是答案了

#include<bits/stdc++.h>
using namespace std;
const int N=3e5+9;
int f[N],ans[N],num[N];
vector<int>e[N];
void dfs1(int u)
{
    num[u]=1;
    for(int i=0;i<e[u].size();i++){
        int v=e[u][i];
        dfs1(v);
        num[u]+=num[v];
    }
}
void dfs2(int u)
{
    ans[u]=u;
    int p=0;
    for(int i=0;i<e[u].size();i++){
        int v=e[u][i];
        dfs2(v);
        if(num[v]>num[e[u][p]])p=i;
    }
    if(e[u].size()>0){
        ans[u]=ans[e[u][p]];
        while(ans[u]!=u){
            if(num[ans[u]]>=num[u]-num[ans[u]])break;
            ans[u]=f[ans[u]];
        }
    }
}
int main()
{
    int n,q;
    cin>>n>>q;
    for(int i=2;i<=n;i++){
        scanf("%d",&f[i]);
        e[f[i]].push_back(i);
    }
    dfs1(1);
    dfs2(1);
    while(q--){
        int x;
        scanf("%d",&x);
        printf("%d\n",ans[x]);
    }
    return 0;
}