KMP字符串匹配算法——PMT数组的计算
Leetcode 28.找出字符串中第一个匹配项的下标
KMP算法和PMT的介绍
KMP算法就是在暴力的基础上,记录之前已经匹配的部分,在失配时,减少重复比较的次数
- 前缀:不包含最后一个字符,包含第一个字符,连续子串
- 后缀:不包含第一个字符,包含最后一个字符,连续子串
- PMT数组:对应字符串的最大前缀与最大后缀相同时的长度
PMT数组的求法(模式匹配的过程)
字符串S与自己进行模式匹配
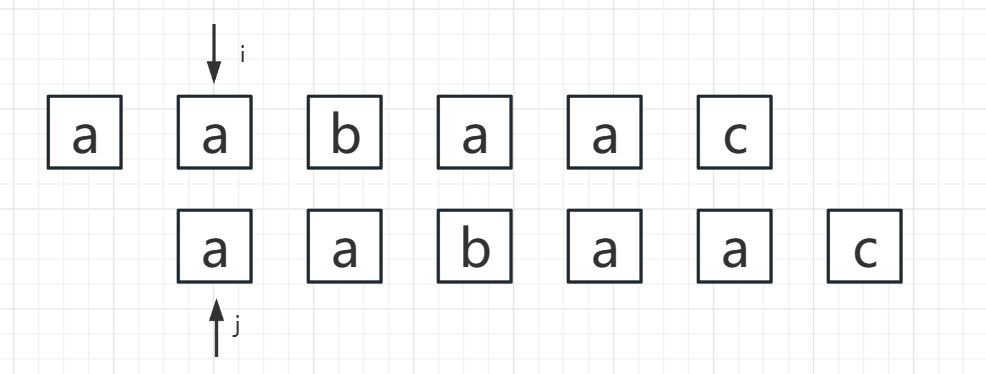
- i:主串的下标,j:模式串的下标
- j < i, i指的是当前字符串的后缀,j指的就是前缀
- PMT[i]:0 ~ i 的最大公共前缀后缀长度
- PMT[0] = 0 (当只有一个字符的时候,前缀和后缀都是空)
匹配规则(直接看具体过程会好理解)
存在的两个问题
- S[i] == S[j] ——> 说明:1 ~ i 与 0 ~ j 匹配成功,此时长度为:i 或 j + 1,选哪个?
- S[i] != S[j] ——> 说明:1 ~ i 与 0 ~ j 匹配失败,此时 j 应该往前移动,j 如何移动?
解决方法
- 在匹配成功之前,是可能出现失配的情况的,此时,匹配上的后缀长度,就不再是从 1 到 i 了,但前缀长度是固定的,都是 0 ~ j,所以当匹配成功时,PMT[i] = j + 1
- 首先 PMT[0...j-1] 都是计算完成的,也就是说失配时,0 ~ j-1 和 i-j ~ i-1 已经匹配成功,0 ~ j-1 的最长公共前缀后缀长度已经求出了,假设为 c,则 0 ~ c-1,和 j-c ~ j-1是相同的,所以此时 j 应该移动到 c ,即:j = PMT[j-1]
- 0 ~ c-1 == j-c ~ j-1 == i-j ~ i-j+C-1 == i-c ~ i-1
- 0 到 c-1,和 i-c 到 i-1 已经匹配成功,所以,下一次该匹配 S[c] 和 S[i]
- j 往前移动时,万一到 0 还未匹配上,此时就会超出有效下标,所以需要特判一下
具体过程
- i = 1,j = 0
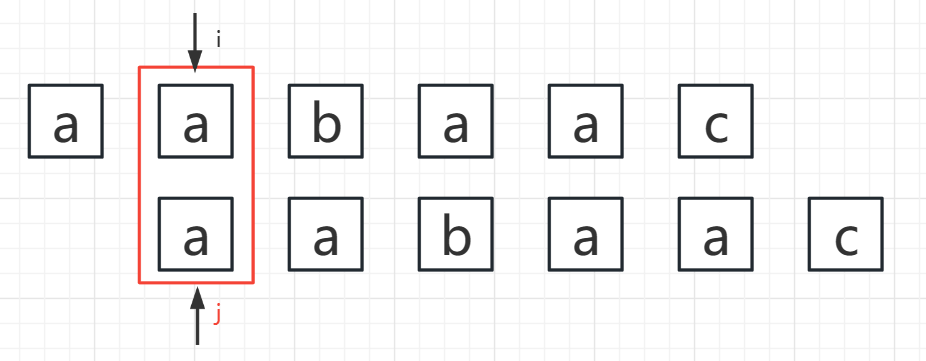
S[i] == S[j] ——> 此时,1 ~ i == 0 ~ j,前缀后缀长度为1,所以 PMT[i] = 1
i,j 同时后移
- i = 2,j = 1
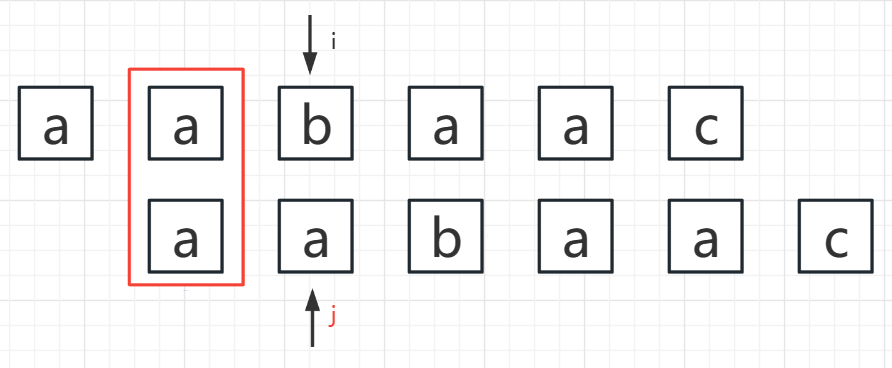
S[i] != S[j] ——> 此时,1 ~ i != 0 ~ j, 前缀后缀收缩,前缀收缩为:2 ~ i,后缀收缩为:0 ~ j-1,S[i] 要与 S[j-1] 比较,...... 能不能利用PMT提高效率?
- i = 2,j = 0
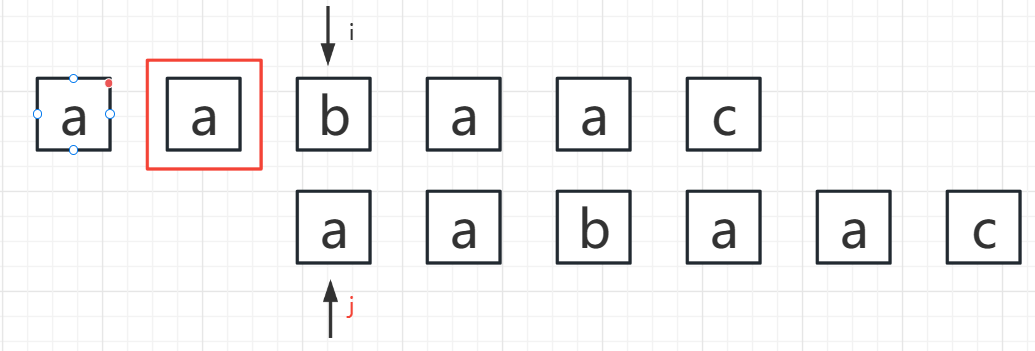
S[i] != S[j] ——> 继续收缩,j 变为 -1,说明收缩到空,最长公共前缀后缀为空,PMT[2] = 0,i++
- i = 3,j = 0
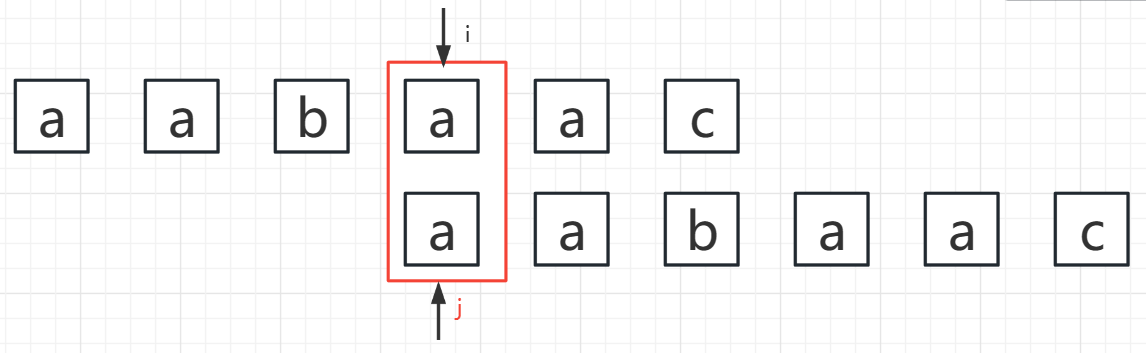
S[i] == S[j] ——> PMT[i] = len(0 ~ j) = j + 1 = 1,i++,j++
- i = 4,j = 1
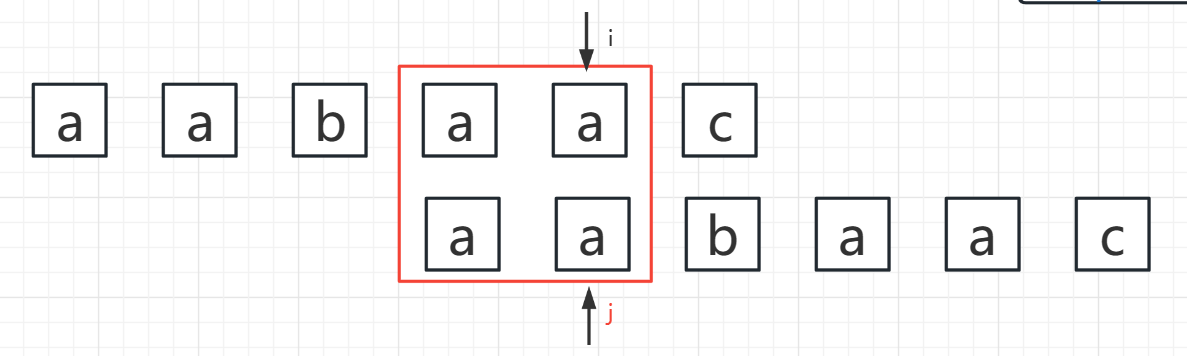
S[i] == S[j] ——> PMT[i] = j + 1 = 2,i++,j++
- i = 5,j = 2
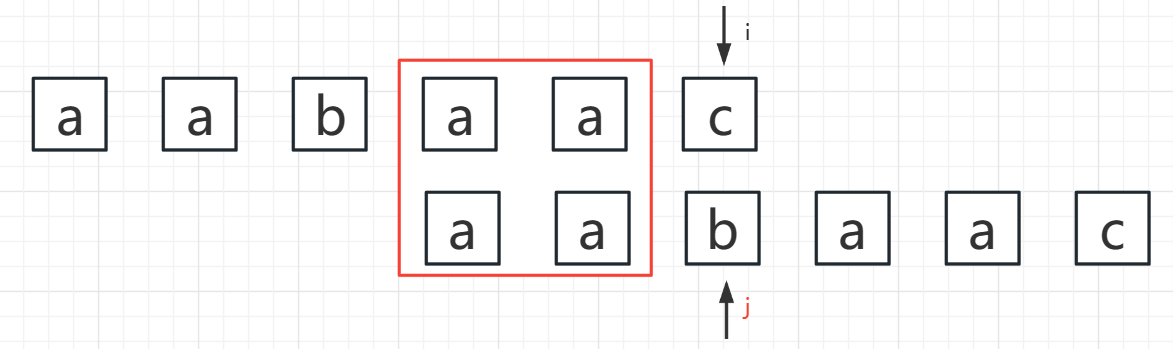
S[i] != S[j] ——> 前缀,后缀开始收缩,但是 0 ~ j-1 与 i-j ~ i-1已经匹配成功,目前已知 0 ~ j-1 的最长公共前缀后缀 c,j 移动到最长公共前缀的后一个,也就是 c,即:j = PMT[j-1] = c = PMT[1] = 1
- i = 5,j = 1
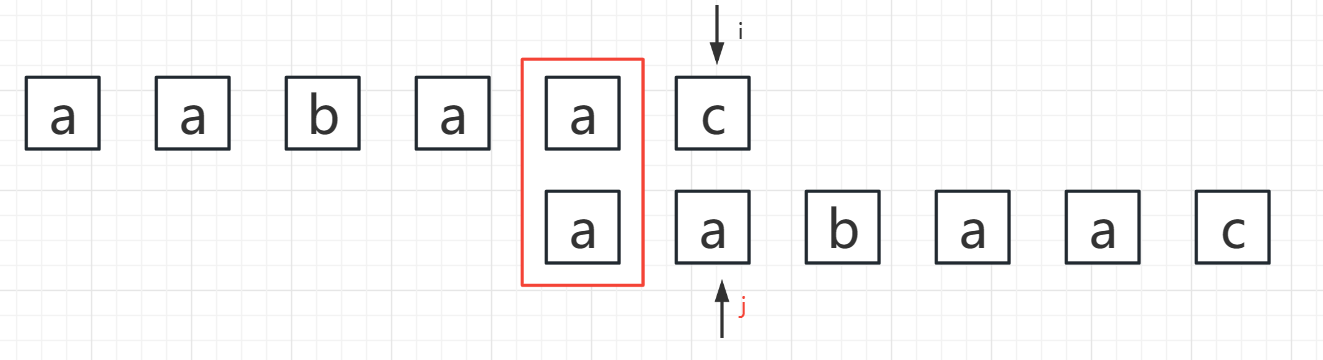
S[i] != S[j] ——> 收缩,j = PMT[j-1] = PMT[0] = 0
- i = 5,j = 0
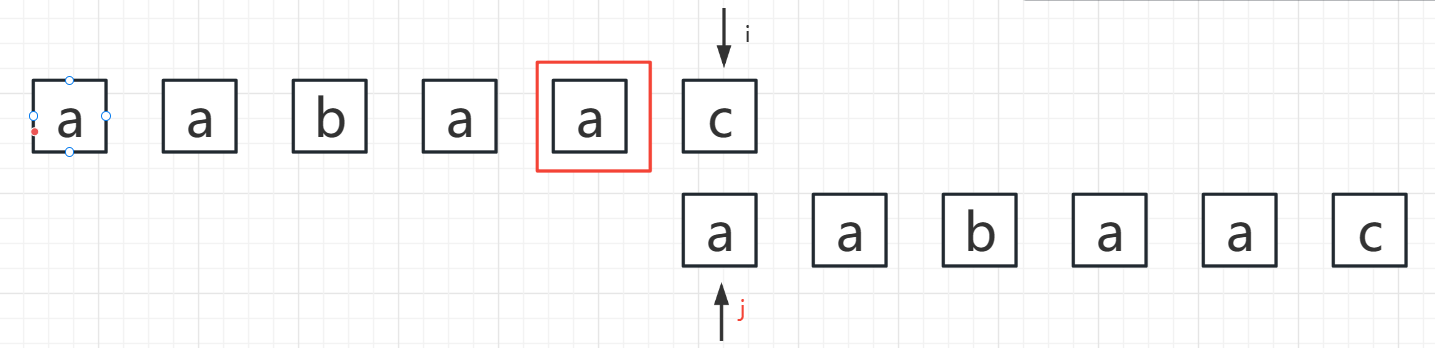
S[i] != S[j] ——> 收缩,此时前缀后缀为空,说明最长公共前缀后缀为空,即:PMT[i] = 0
总结与代码实现
总结
- PMT[0] = 0,i = 1,j = 0
- S[i] == S[j],PMT[i] = j+1,i++,j++
- S[i] != S[j], j > 0,j = PMT[j-1],返回步骤2
- S[i] != S[j],j == 0,PMT[i] = 0,i++
代码实现
GO实现
func GetPMT(needle string) []int {
pmt := make([]int, len(needle))
i := 1
j := 0
for i < len(needle) {
if needle[i] == needle[j] {
pmt[i] = j + 1
j++
i++
} else {
for needle[i] != needle[j] {
if j > 0 {
j = pmt[j-1]
} else {
pmt[i] = 0
i++
break
}
}
}
}
return pmt
}



