KMP算法（详解）
KMP算法
解决的问题就是在字符串（也叫主串）中的模式（pattern）定位问题。
说简单点就是我们平时常说的关键字搜索。模式串就是关键字（接下来称它为P），如果它在一个主串（接下来称为T）中出现，就返回它的具体位置，否则返回-1（常用手段）。
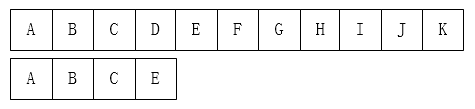
首先，对于这个问题有一个很单纯的想法
Brute-Force（暴力）算法：从左到右一个个匹配，如果这个过程中有某个字符不匹配，就跳回去，将模式串向右移动一位。
我们可以这样初始化：
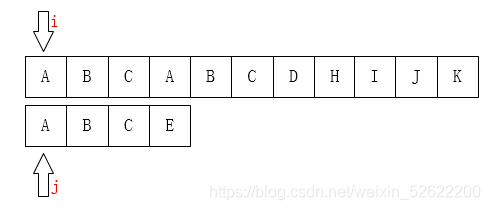
之后我们只需要比较i指针指向的字符和j指针指向的字符是否一致。如果一致就都向后移动，如果不一致，如下图：
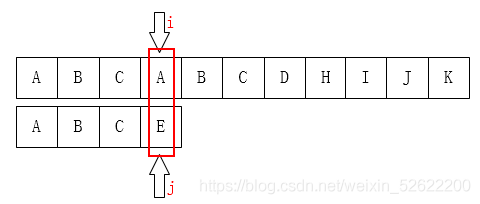
A和E不相等，那就把i指针移回第1位（假设下标从0开始），j移动到模式串的第0位，然后又重新开始这个步骤：
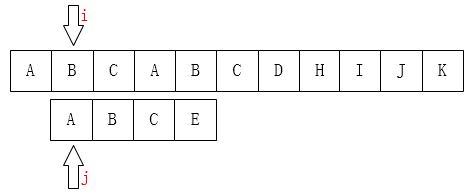
基于这个想法我们可以得到以下的程序：
# 字符串匹配的暴力解法
def brute_force(ts, ps):
t = [c for c in ts]
p = [c for c in ps]
i = 0 # 主串的位置
j = 0 # 模式串的位置
while i < len(t) and j < len(p):
if t[i] == p[j]: # 当两个相同，就比较下一个
i += 1
j += 1
else:
i = i - j + 1 # 一旦不匹配，i后退
j = 0
if j == len(p):
return i - j # 返回主串的开始位置
else:
return -1
上面的程序是没有问题的，但不够好！
如果是人为来寻找的话，肯定不会再把i移动回第1位，因为主串匹配失败的位置前面除了第一个A之外再也没有A了，我们为什么能知道主串前面只有一个A？因为我们已经知道前面三个字符都是匹配的！（这很重要）。移动过去肯定也是不匹配的！有一个想法，i可以不动，我们只需要移动j即可，如下图：
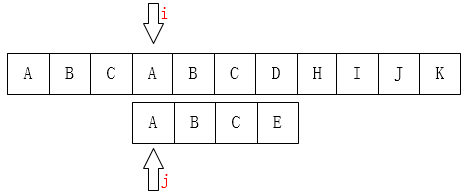
上面的这种情况还是比较理想的情况，我们最多也就多比较了再次。但假如是在主串“SSSSSSSSSSSSSA”中查找“SSSSB”，比较到最后一个才知道不匹配，然后i回溯，这个的效率是显然是最低的。
提取加速匹配的信息
KMP 算法主要是通过消除主串指针的回溯来提高匹配的效率
利用已经部分匹配这个有效信息，保持i指针不回溯，通过修改j指针，让模式串尽量地移动到有效的位置。
所以，整个KMP的重点就在于当某一个字符与主串不匹配时，我们应该知道j指针要移动到哪？
接下来我们自己来发现j的移动规律
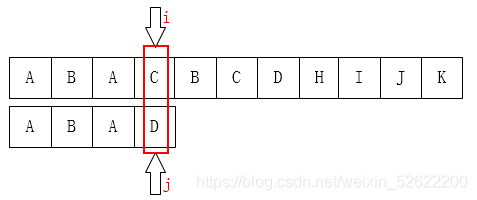
如图：C和D不匹配了，我们要把j移动到哪？显然是第1位。为什么？因为前面有一个A相同啊
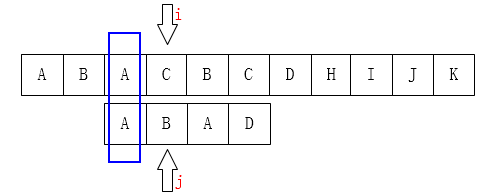
如下图也是一样的情况：
可以把j指针移动到第2位，因为前面有两个字母是一样的：
至此我们可以大概看出一点端倪，当匹配失败时，j要移动的下一个位置k。
存在着这样的性质：最前面的k个字符和j之前的最后k个字符是一样的。
如果用数学公式来表示是这样的:
P[0 ~ k-1] == P[j-k ~ j-1]
这个相当重要，如果觉得不好记的话，可以通过下图来理解：
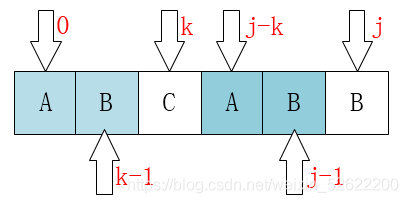
弄明白了这个就应该可能明白为什么可以直接将j移动到k位置了。
因为:
当T[i] != P[j]时
有T[i-j ~ i-1] == P[0 ~ j-1]
由P[0 ~ k-1] == P[j-k ~ j-1]
必然：T[i-k ~ i-1] == P[0 ~ k-1]
怎么求这个（这些）k呢？因为在P的每一个位置都可能发生不匹配，也就是说我们要计算每一个位置j对应的k，所以用一个数组next来保存，next[j] = k，表示当T[i] != P[j]时，j指针的下一个位置。
def get_next(ps):
p = [c for c in ps]
next = [-1] * len(p)
next[0] = -1
j = 0
k = -1
while j < len(p) - 1:
if k == -1 or p[j] == p[k]:
j += 1
k += 1
next[j] = k
else:
k = next[k]
return next
这个版本的求next数组的算法应该是流传最广泛的，代码是很简洁。可是真的很让人摸不到头脑，它这样计算的依据到底是什么？
现在要始终记住一点，next[j]的值（也就是k）表示，当P[j] != T[i]时，j指针的下一步移动位置。
先来看第一个：当j为0时，如果这时候不匹配，怎么办？
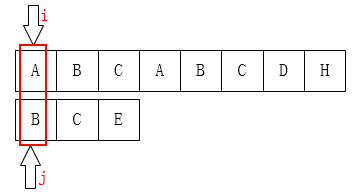
像上图这种情况，j已经在最左边了，不可能再移动了，这时候要应该是i指针后移。所以在代码中才会有next[0] = -1;这个初始化。
如果是当j为1的时候呢？
显然，j指针一定是后移到0位置的。因为它前面也就只有这一个位置了
下面这个是最重要的，请看如下图：
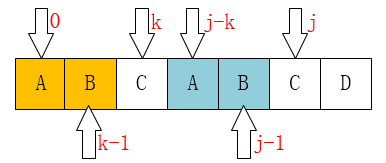
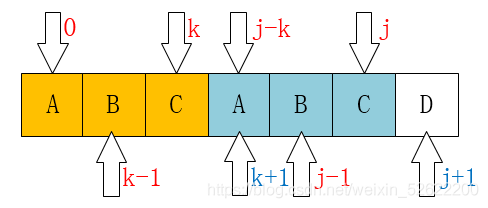
请仔细对比这两个图。
我们发现一个规律：
当P[k] == P[j]时，
有next[j+1] == next[j] + 1
其实这个是可以证明的：
因为在P[j]之前已经有P[0 ~ k-1] == p[j-k ~ j-1]。（next[j] == k）
这时候现有P[k] == P[j]，我们是不是可以得到P[0 ~ k-1] + P[k] == p[j-k ~ j-1] + P[j]。
即：P[0 ~ k] == P[j-k ~ j]，即next[j+1] == k + 1 == next[j] + 1。
这里的公式不是很好懂，还是看图会容易理解些。
那如果P[k] != P[j]呢？比如下图所示：
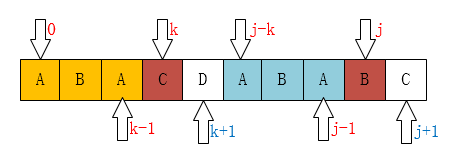
像这种情况，如果你从代码上看应该是这一句：k = next[k];为什么是这样子？你看下面应该就明白了
现在你应该知道为什么要k = next[k]了吧！像上边的例子，我们已经不可能找到[ A，B，A，B ]这个最长的后缀串了，但我们还是可能找到[ A，B ]、[ B ]这样的前缀串的。所以这个过程像不像在定位[ A，B，A，C ]这个串，当C和主串不一样了（也就是k位置不一样了），那当然是把指针移动到next[k]啦。
有了next数组之后就一切好办了，我们可以动手写KMP算法了：
def kmp(ts, ps):
t = [c for c in ts]
p = [c for c in ps]
i, j = 0, 0
next = get_next(ps)
while i < len(t) and j < len(p):
if j == -1 or t[i] == p[j]: # 当j为-1时，要移动i，j需要归零
i += 1
j += 1
else:
j = next[j] #j回到指定的位置
if j == len(p):
return i - j
else:
return -1
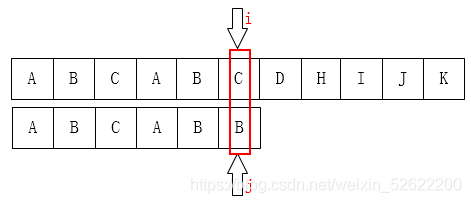
最后，来看一下上边的算法存在的缺陷。来看第一个例子
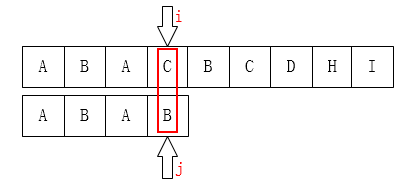
显然，当我们上边的算法得到的next数组应该是[ -1，0，0，1 ]
所以下一步我们应该是把j移动到第1个元素咯：
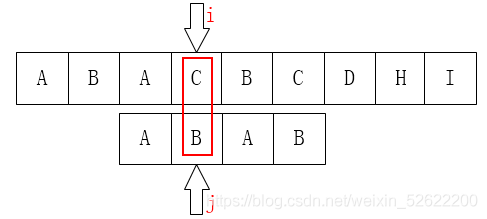
不难发现，这一步是完全没有意义的。因为后面的B已经不匹配了，那前面的B也一定是不匹配的，同样的情况其实还发生在第2个元素A上。
显然，发生问题的原因在于P[j] == P[next[j]]。
所以我们也只需要添加一个判断条件即可：
def get_next(ps):
p = [c for c in ps]
next = [-2] * len(p)
next[0] = -1
j = 0
k = -1
while j < len(p) - 1:
if k == -1 or p[j] == p[k]:
j += 1
k += 1
if p[j] == p[k]: # 当两个字符相等时，要跳过
next[j] = next[k]
else:
next[j] = k
else:
k = next[k]
return next
另外求解：
class Solution:
def kmp(self , S: str, T: str) -> int:
# write code here
if S == '':
return 0
n = len(S)
m = len(T)
next = [0] * n
count = 0
j = 0
for i in range(1, n):
while j > 0 and S[j] != S[i]:
j = next[j - 1]
if S[j] == S[i]:
j += 1
next[i] = j
j = 0
for i in range(m):
while j > 0 and S[j] != T[i]:
j = next[j - 1]
if S[j] == T[i]:
j += 1
if j == n:
count += 1
j = next[j - 1]
return count
