逻辑回归
LogisticRegression逻辑回归
引言:
机器学习 解决的问题,大体上分为两种 预测 和 分类。
预测: 一般采用是回归模型,比如最常用的 线性回归;
分类:采用的有 决策树,KNN, 支持向量机, 朴素贝叶斯等等模型。
其实本质上来讲是一样的,都是通过对已有数据的学习,构建模型,然后对未知的数据进行预测,若是连续的数值预测就是回归问题,若是离散的类标号预测,就是分类问题。
这里面有一类比较 特殊 的算法,就是逻辑回归(logistic regression) 。它叫“回归”,可见基本思路还是回归的那一套,同时,逻辑回归又是标准的解决分类问题的模型。换句话说,逻辑回归是用与回归类似的思路解决了分类问题
阶跃函数
现在有n个数据元组{X1, X2, X3, ..., Xn},每个数据元组对应了一个类标号yi,同时每个数据元组Xi有m个属性,假设现在面临的是一个简单二分类问题,类标号为0, 1两种。如果使用简单的回归方法对已知数据进行曲线拟合,得到如下线性方程:
z = f(x) = w0 + w1*x1 + ...+ wm * xm
注: 并不是说回归只能解决二分类问题, 但是用到多分类时,算法并没有发生变化, 只是用的次数更多了而已
实际上,逻辑回归分类的办法与SVM是一致的,都是在空间中找到曲线,将数据点按相对曲线的位置,分成上下两类。
也就是说,对于任意测试元组X, f(x)可以根据其正负性而得到类标号。直接依靠拟合曲线的函数值是不能得到类标号的,还需要一种理想的“阶跃函数”,将函数值按照正负性分别映射为0,1类标号。这样的阶跃函数ϕ(z)如下表示
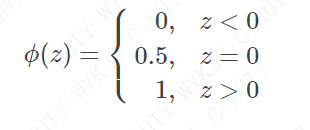
然而,直接这样设计阶跃函数不方便后面的优化计算,因为函数值不连续,无法进行一些相关求导。所以,逻辑回归中,大家选了一个统一的函数,也就是Sigmoid函数,如公式(1)所示:
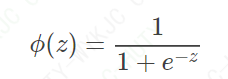
Sigmoid函数的图像如下图所示,当z>0时,Sigmoid函数大于0.5;当z<0时,Sigmoid函数小于0.5。所以,我们可以将拟合曲线的函数值带入Sigmoid函数,观察ϕ(z)与0.5的大小确定其类标号
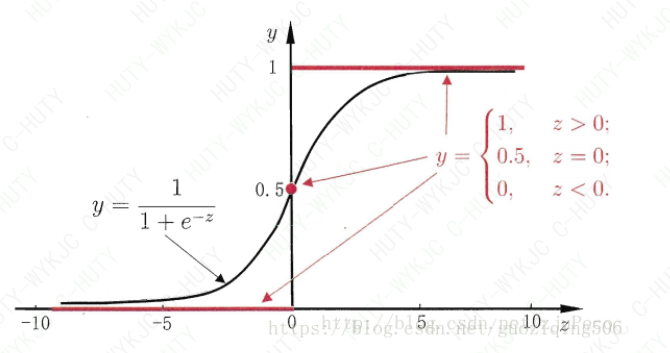
Sigmoid函数还有一个好处,那就是因为其取值在0,1之间。所以可以看做是测试元组属于类1的后验概率,即p(y=1|X)p(y=1|X)。其实这一点从图像也可以看出来:zz的值越大,表明元组的空间位置距离分类面越远,他就越可能属于类1,所以图中zz越大,函数值也就越接近1;同理,zz越小,表明元组越不可能属于类1.
代价函数
阶跃函数告诉我们,当得到拟合曲线的函数值时,如何计算最终的类标号。但是核心问题仍然是这个曲线如何拟合。既然是回归函数,我们就模仿线性回归,用误差的平方和当做代价函数。代价函数如公式(2)所示:
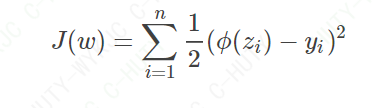
其中,zi=WTXi+w0zi=WTXi+w0,yi为Xi真实的类标号。按说此时可以对代价函数求解最小值了,但是如果你将ϕ(z)=1/(1+e^(-z)), 带入公式(2)的话,那么当前代价函数的图像是一个非凸函数,非凸函数有不止一个极值点,导致不容易做最优化计算。也就是说,公式(2)的这个代价函数不能用。(凸函数的应用可以,关联到最大期望算法)
那自然要想办法设计新的代价函数。我们在上面说了,ϕ(z)的 取值 可以看做是测试元组属于类1的 后验概率,所以可以得到下面的结论:
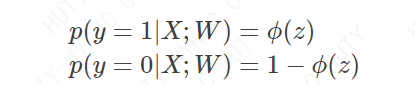
更进一步,上式也可以这样表达:

公式(3)表达的含义是在参数W下,元组类标号为y的后验概率。假设现在已经得到了一个抽样样本,那么联合概率∏ni=1p(yi|Xi;W)∏i=1np(yi|Xi;W)的大小就可以反映模型的代价:联合概率越大,说明模型的学习结果与真实情况越接近;联合概率越小,说明模型的学习结果与真实情况越背离。
而对于这个联合概率,我们可以通过计算 参数的最大似然估计 的那一套方法来确定使得联合概率最大的参数W,此时的W就是我们要选的最佳参数,它使得联合概率最大(即代价函数最小),下面看具体的运算步骤。
逻辑回归步骤:
有上述可知:
逻辑回归本质: 极大似然估计
写出最大似然函数,并进行对数化处理
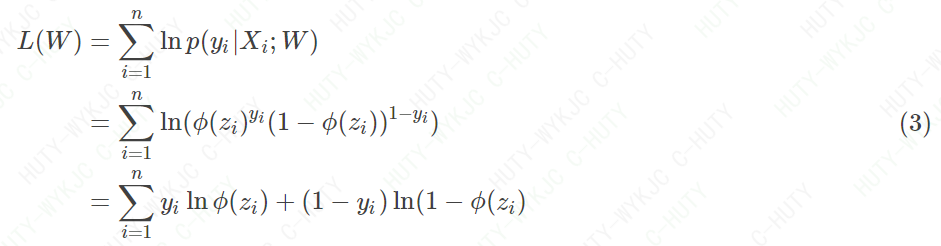
通过上面的分析,显然−L(W)就是代价函数J(W)。为方便后面的推导,我把J(W)也写出来:

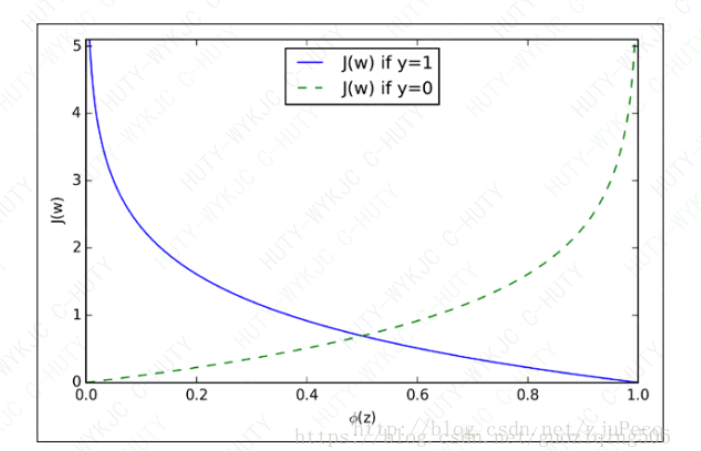
可以看出,如果类标号为1,那么ϕ(z)的取值在[0,1]范围内增大时,代价函数减小,说明越接近真实情况,代价就越小;如果类标号为0,也是一样的道理
用梯度下降方法计算代价函数最小值
如果能求出代价函数的最小值,也就是最大似然函数的最大值。那么得到的权重向量W就是逻辑回归的最终解。但是通过上面的图像,你也能发现,J(W)是一种非线性的S型函数,不能直接利用偏导数为0求解。于是我们采用梯度下降法
首先,根据梯度的相关理论,我们知道梯度的负方向就是代价函数下降最快的方向。因此,我们应该沿着梯度负方向逐渐调整权重分量wj,直到得到最小值,所以每个权重分量的变化应该是这样的
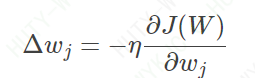
其中η为学习率,控制步长。而∂J(W)/∂wj可以如下计算:
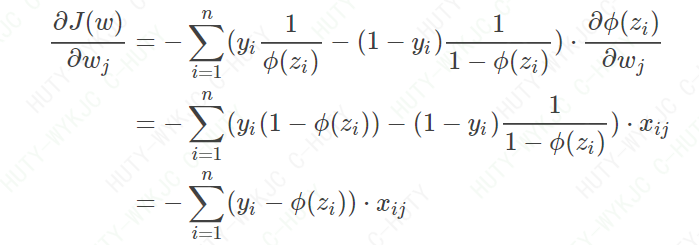
上式的推导中用到了Sigmoid函数ϕ(z)的一个特殊的性质:

这样,我们就得到了梯度下降法更新权重的变量

最后,说一下权重向量的初始化问题。一般用接近于0的随机值初始化wjwj,比如在区间[−0.01,0.01]内均匀选取。这样做的理由是如果wi很大,则加权和可能也很大,根据Sigmoid函数的图像(即本文的第一个图像)可知,大的加权和会使得ϕ(zi)的导数接近0,则变化速率变缓使得权重的更新变缓。
#!/usr/bin/env python3
# -*- coding:utf-8 -*-
"""
Logistic回归梯度上升优化算法
"""
import numpy as np
import random
def loadDataSet(filePath):
dataMat = []
labelMat = []
fr = open(filePath)
for line in fr.readlines():
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
labelMat.append(int(lineArr[2]))
return dataMat, labelMat
def sigmoid(intX):
"""
sigmoid 函数
:param intX:
:return:
"""
return 1.0 / (1 + np.exp(-intX))
def gradAscent(dataMatIn, classLabels):
"""
梯度上升算法
:param dataMatIn: 二维numpy数组,每一列代表不同的特征
:param classLabels:
:return:
"""
dataMatrix = np.mat(dataMatIn)
labelMat = np.mat(classLabels).transpose() # 计算矩阵转置
m, n = np.shape(dataMatrix)
alpha = 0.001 # 步长
maxCycles = 500 # 迭代次数
weights = np.ones((n, 1)) # 初始权重
# 循环更新权重
for k in range(maxCycles):
h = sigmoid(dataMatrix * weights)
error = (labelMat - h)
weights = weights + alpha * dataMatrix.transpose() * error
return weights
def randomGradAscent(dataMatrix, classLabels):
"""
随机梯度上升算法
:param dataMatrix:
:param classLabels:
:return:
"""
m, n = np.shape(dataMatrix)
alpha = 0.001
weights = np.ones(n)
for i in range(m):
h = sigmoid(np.sum(dataMatrix[i] * weights))
error = classLabels[i] - h
weights = weights + alpha * error * dataMatrix[i]
return weights
def stocGradAscent(dataMatrix, classLabels, numIter=150):
"""
随机梯度上升算法,在大量迭代后达到了稳定值,但是在存在一些小的周期性波动
产生这一现象原因,数据集并非线性可分,
解决部分数据线性不可分,加快收敛速度
:param dataMatrix:
:param classLabels:
:param numIter:
:return:
"""
m, n = np.shape(dataMatrix)
weights = np.ones(n)
for j in range(numIter):
dataIndex = range(m)
for i in range(m):
alpha = 4 / (1.0 + j + i) + 0.01 # alpha 每次迭代时进行调整
randIndex = int(random.uniform(0, len(dataIndex)))
h = sigmoid(np.sum(dataMatrix[randIndex] * weights))
error = classLabels[randIndex] - h
weights = weights + alpha * error * dataMatrix[randIndex]
del(dataIndex[randIndex])
return weights
# 疝气病症预测病马的死亡率
def classifyVector(intX, weights):
prob = sigmoid(np.sum(intX*weights))
if prob > 0.5:
return 1
else:
return 0
def colicTest(trainFilePath="D:\\workplace\\data\\tensorflow\\logistic_data\\horse-colic.data",
testFilePath="D:\\workplace\data\\tensorflow\\logistic_data\\horse-colic.test"):
frTrain = open(trainFilePath)
frTest = open(testFilePath)
trainingSet = []
trainingLabels = []
for line in frTrain.readlines():
currLine = line.strip().split()
lineArr = []
for i in range(21):
lineArr.append(float(currLine[i]))
trainingSet.append(lineArr)
trainingLabels.append(float(currLine[21]))
trainWeights = stocGradAscent(np.array(trainingSet), trainingLabels, 500)
errorCount = 0
numTestVec = 0
for line in frTest.readlines():
numTestVec += 1
currLine = line.strip().split('\t')
lineArr = []
for i in range(21):
lineArr.append(float(currLine[i]))
if int(classifyVector(np.array(lineArr), trainWeights)) != int(currLine[21]):
errorCount += 1
errorRate = (float(errorCount) / numTestVec)
print(f'the error rate of this test is : {errorRate}')
return errorRate
def multiTest():
numTests = 10
errorSum = 0
for k in range(numTests):
errorSum += colicTest()
print(f'after {numTests} iterations the averages error rate is : {errorSum/float(numTests)}')
if __name__ == '__main__':
multiTest()
参考链接:
https://blog.csdn.net/guoziqing506/article/details/81328402
https://blog.csdn.net/zjuPeco/article/details/77165974



