POJ 1185 炮兵阵地 【状压DP】

<题目链接>

题目大意：

司令部的将军们打算在N*M的网格地图上部署他们的炮兵部队。一个N*M的地图由N行M列组成，地图的每一格可能是山地（用"H" 表示），也可能是平原（用"P"表示），如下图。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示： 

                                                 

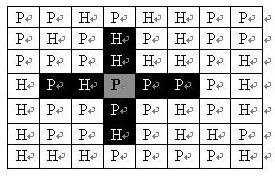
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 
现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

输入：

第一行包含两个由空格分割开的正整数，分别表示N和M； 
接下来的N行，每一行含有连续的M个字符('P'或者'H')，中间没有空格。按顺序表示地图中每一行的数据。N <= 100；M <= 10。

输出：

仅一行，包含一个整数K，表示最多能摆放的炮兵部队的数量。

解题分析：

从形式和数据范围来看，不难看出是一道状压DP的题。因为第$i$行与前两行的状态有关，所以我们这里用$dp[i][j][k]$来表示第$i$行为第$j$种状态，$k$则表示上一行的状态。

#include <cstdio>
#include <algorithm>
using namespace std;

const int MAXR = 110, MAXC = 15, MAXM = 70;
#define legal(a,b) a&b

int n,m,top;
int base[MAXR],state[MAXM],num[MAXM],dp[MAXR][MAXM][MAXM]; //dp[i][j][k]，表示第i行，j表示第i行的状态，k表示第i-1行的状态
char graph[MAXR][MAXC]; 

inline bool ok(int x){      //在同一行的角度下，先判断这个状态是否可行
    if(x&(x<<1) || x&(x<<2))return false;
    return true;
}
inline int Count(int x){     //计算这个状态下，该行所放士兵的数量
    int ans=0;
    while(x){
        ans+=x&1;
        x>>=1;
    }return ans;
}
inline void init(){
    top=0;
    for(int i=0;i<(1<<m);i++){
        if(!ok(i))continue;
        num[top]=Count(i);     //记录每个状态对应士兵的数量
        state[top++]=i;        //预处理出初始的所有可行状态
    }
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=0;i<n;i++){
        scanf("%s",graph[i]);
        for(int j=0;j<m;j++)
            if(graph[i][j]=='H')base[i]+=1<<j;
    }
    init();
    for(int i=0;i<top;i++){     //初始化第一行
        if(legal(state[i],base[0]))continue;
        dp[0][i][0]=num[i];
    }
    for(int i=0;i<top;i++){    //初始化第二行 ,i表示第二行的状态
        if(legal(state[i],base[1]))continue;
        for(int j=0;j<top;j++){    //j表示第一行的状态
            if(legal(state[j],base[0]))continue;
            if(legal(state[i],state[j]))continue;
            dp[1][i][j]=max(dp[1][i][j],dp[0][j][0]+num[i]);
        }
    }

    for(int r=2;r<n;r++){    //枚举第r行
        for(int i=0;i<top;i++){    //第r行的状态
            if(legal(state[i],base[r]))continue;
            for(int j=0;j<top;j++){    //第r-1行的状态
                if(legal(state[j],base[r-1]))continue;
                if(legal(state[i],state[j]))continue;
                for(int k=0;k<top;k++){     //第r-2行的状态
                    if(legal(state[k],base[r-2]))continue;
                    if(legal(state[j],state[k]))continue;
                    if(legal(state[i],state[k]))continue;
                    dp[r][i][j]=max(dp[r][i][j],dp[r-1][j][k]+num[i]);
                }
            }
        }
    }
    int ans=0;
    for(int i=0;i<top;i++)
        for(int j=0;j<top;j++)
            ans=max(ans,dp[n-1][i][j]);    //从最后一行的所有状态中挑选一个最大的
    printf("%d\n",ans);
}