树上差分
树上差分
首先,什么是差分呢?
差分,又名差分函数或差分运算,差分的结果反映了离散化之间的一种变化,是研究离散数学的一种工具,常用函数差近似导数。(感谢bai度百科)
说人话,在数组中就是后一个数减去前一个数的值搞到一个集合里,这玩意儿就是差分数组。
那么,什么是树上差分呢?
树上差分,顾名思义,就是在树上进行差分,以起到优化复杂度的目的。主要作用是对树上的路径进行修改和查询操作,在修改多、查询少的情况下复杂度比较优秀。当然这类问题也可以通过其他手段解决,但是呢,树上差分十分的简洁,可以避免调很久玄学错误。
先来一道例题banziti
题目意思大概就是给你一棵树,然后再给你几组起点终点,起点终点的树上距离经过的每一个点都要+1。求最大点权。
怎么用树上差分解决这个问题呢?如果起点x,终点y,就先开一个新的数组a[],然后在a[x]处+1,a[y]处+1,a[LCA(x,y)]处-1,a[fa[LCA(x,y)]]处-1,再将每一个a[p]点(1≤p≤n)更新为它和它儿子的点权之和。这时每一个点的a[]值就是它们的访问次数了。
代码如下:
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int SIZE=500009; 4 5 int n,m,ans; 6 int cnt,tot; 7 int head[SIZE],nex[SIZE*2],to[SIZE*2],a[SIZE]; 8 int size[SIZE],d[SIZE],fa[SIZE],dfn[SIZE],rev[SIZE],son[SIZE],top[SIZE]; 9 10 void add(int u,int v){ 11 to[++tot]=v; 12 nex[tot]=head[u];head[u]=tot; 13 } 14 15 void dfs(int x,int f){ 16 size[x]=1;fa[x]=f;d[x]=d[f]+1; 17 for(int i=head[x];i;i=nex[i]){ 18 int y=to[i]; 19 if(y==f) continue; 20 dfs(y,x); 21 size[x]+=size[y]; 22 if(size[son[x]]<size[y]) son[x]=y; 23 } 24 } 25 void dfs2(int x){ 26 if(son[fa[x]]!=x){top[x]=x;} 27 else{top[x]=top[fa[x]];} 28 dfn[++cnt]=x; 29 rev[x]=cnt; 30 if(son[x]) dfs2(son[x]); 31 for(int i=head[x];i;i=nex[i]){ 32 int y=to[i]; 33 if(y==fa[x]||y==son[x]) continue; 34 dfs2(y); 35 } 36 } 37 int LCA(int x,int y){ 38 if(d[x]<d[y]) swap(x,y); 39 while(top[x]!=top[y]){ 40 if(d[top[x]]<d[top[y]]) swap(x,y); 41 x=fa[top[x]]; 42 } 43 if(d[x]>d[y]) swap(x,y); 44 return x; 45 } 46 void dfss(int x,int f){ 47 for(int i=head[x];i;i=nex[i]){ 48 int y=to[i]; 49 if(y==f) continue; 50 dfss(y,x); 51 a[x]+=a[y]; 52 } 53 } 54 int main(){ 55 d[1]=1; 56 cin>>n>>m; 57 for(int i=1;i<n;i++){ 58 int u,v; 59 cin>>u>>v; 60 add(u,v); 61 add(v,u); 62 } 63 dfs(1,0); 64 dfs2(1); 65 for(int i=1;i<=m;i++){ 66 int x,y; 67 cin>>x>>y; 68 int kkk=LCA(x,y); 69 a[x]++;a[y]++; 70 a[kkk]--; 71 a[fa[kkk]]--; 72 } 73 dfss(1,0); 74 for(int i=1;i<=n;i++) ans=max(ans,a[i]); 75 cout<<ans; 76 return 0; 77 }
再来一道闇の連鎖
每一条附加边都有以下性质,它们都使得原图搞成一个环,而每一条附加边的两个端点总是在图上。
先分类讨论各种情况,如果第一次切断的是不在环上的边,那么我们任意切掉一条附加边就可以完成任务,答案ans+=不在环上的边的数量*M。如果第一次切断的是只连着一条附加边的边,那么我们切掉该附加边就可达成杀死闇の連鎖的目的ans+=只连着一条附加边的边的数量。如果第一次切断的是连着多条附加边的边,那么对不起,没有任何办法,无法杀死闇の連鎖。
所以我的问题转化成了如何求以上数据(不在环上的边的数量,只连着一条附加边的边的数量)。
因为附加边具有最开始描述的(指斜体部分)性质。我们想到了树上差分!每当出现一条附加边,我就将它的两个端点在树上最短路所经过的边的边权+1,处理边权的最常用方式就是将边权下放。访问时如果a[p]=0(2≤p≤n)ans+=M;访问时如果a[p]=1(2≤p≤n)ans+=1。最后输出ans就对了。
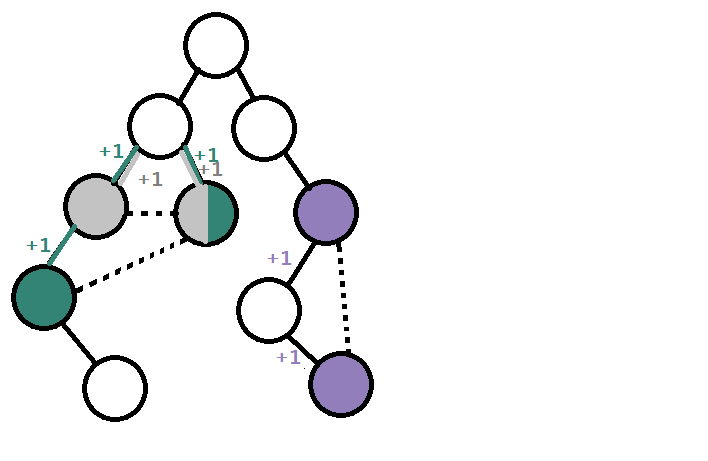
接下来是可可爱爱的代码啦~
1 #include<bits/stdc++.h> 2 using namespace std; 3 4 const int SIZE=200009; 5 int n,m,ans,tot,cnt; 6 int head[SIZE],nex[SIZE*2],to[SIZE*2],a[SIZE]; 7 int siz[SIZE],d[SIZE],fa[SIZE],dfn[SIZE],rev[SIZE],son[SIZE],top[SIZE]; 8 9 void add(int u,int v){ 10 to[++tot]=v; 11 nex[tot]=head[u];head[u]=tot; 12 } 13 14 void dfs(int x,int f){ 15 siz[x]=1;fa[x]=f;d[x]=d[f]+1; 16 for(int i=head[x];i;i=nex[i]){ 17 int y=to[i]; 18 if(y==f) continue; 19 dfs(y,x); 20 siz[x]+=siz[y]; 21 if(siz[son[x]]<siz[y]) son[x]=y; 22 } 23 } 24 void dfs2(int x){ 25 if(son[fa[x]]!=x){top[x]=x;} 26 else{top[x]=top[fa[x]];} 27 dfn[++cnt]=x; 28 rev[x]=cnt; 29 if(son[x]) dfs2(son[x]); 30 for(int i=head[x];i;i=nex[i]){ 31 int y=to[i]; 32 if(y==fa[x]||y==son[x]) continue; 33 dfs2(y); 34 } 35 } 36 int LCA(int x,int y){ 37 if(d[x]<d[y]) swap(x,y); 38 while(top[x]!=top[y]){ 39 if(d[top[x]]<d[top[y]]) swap(x,y); 40 x=fa[top[x]]; 41 } 42 if(d[x]>d[y]) swap(x,y); 43 return x; 44 } 45 46 void dfss(int x,int f){ 47 for(int i=head[x];i;i=nex[i]){ 48 int y=to[i]; 49 if(y==f) continue; 50 dfss(y,x); 51 a[x]+=a[y]; 52 } 53 } 54 55 signed main(){ 56 cin>>n>>m; 57 for(int i=1;i<n;i++){ 58 int u,v; 59 cin>>u>>v; 60 add(u,v);add(v,u); 61 } 62 dfs(1,0); 63 dfs2(1); 64 for(int i=1;i<=m;i++){ 65 int x,y,z; 66 cin>>x>>y; 67 z=LCA(x,y); 68 a[x]++;a[y]++;a[z]-=2; 69 } 70 dfss(1,0); 71 for(int i=2;i<=n;i++){ 72 if(a[i]==0) ans+=m; 73 else if(a[i]==1) ans++; 74 } 75 cout<<ans; 76 return 0; 77 }
很快啊,就A了道困难题
总结一下,单说树上差分这种思想的话,那可真是非常简单啊,可是你做题的时候压根想不到用树上差分啊。aaaaaaaxxxxxxxbbbbbbb


