tensorflow 莫烦教程
1,感谢莫烦
2,第一个实例:用tf拟合线性函数
import tensorflow as tf import numpy as np # create data x_data = np.random.rand(100).astype(np.float32) y_data = x_data*0.1 + 0.3 #先创建我们的线性函数目标 #搭建模型 Weights = tf.Variable(tf.random_uniform([1], -1.0, 1.0)) biases = tf.Variable(tf.zeros([1])) y = Weights*x_data + biases #计算误差,然后根据误差调节loss loss = tf.reduce_mean(tf.square(y-y_data)) optimizer = tf.train.GradientDescentOptimizer(0.5) train = optimizer.minimize(loss) #我们的目标是让误差尽量小 init = tf.global_variables_initializer() # 注册和初始化变量 sess = tf.Session() #创建会话, sess.run(init) # 开始运行。tf需要在会话里运行,原因不明 for step in range(201): sess.run(train) if step % 20 == 0: #每训练一段时间打印一下结果 print(step, sess.run(Weights), sess.run(biases))
3,会话控制session
import tensorflow as tf # create two matrixes matrix1 = tf.constant([[3,3]]) #tf.constant表示常量 matrix2 = tf.constant([[2], [2]]) product = tf.matmul(matrix1,matrix2) #两个同类型是数相乘,不同于tf.multiply(),这只是表示运算的步骤,而不是过程 #要想运行两个数相乘得到结果,有以下两种方法
# method 1 sess = tf.Session() result = sess.run(product) print(result) sess.close() # method 2 with tf.Session() as sess: result2 = sess.run(product) print(result2)
4,变量Variable
和python不一样的是,tf中只有定义了是变量的才是变量,这一点和一直以来的习惯不一样
语法:
import tensorflow as tf state = tf.Variable(0, name='counter') # 定义常量 one one = tf.constant(1) # 定义加法步骤 (注: 此步并没有直接计算) new_value = tf.add(state, one) # 将 State 更新成 new_value update = tf.assign(state, new_value) #但是以上步骤没有一步是直接运算的,要运算还需要载入变量 init = tf.global_variables_initializer() #激活变量是这样滴 #激活以后还是需要放在会话中运行 with tf.Session() as sess: sess.run(init) for _ in range(3): sess.run(update) print(sess.run(state))
5,placeholder传入值
import tensorflow as tf #在 Tensorflow 中需要定义 placeholder 的 type ,一般为 float32 形式 input1 = tf.placeholder(tf.float32) input2 = tf.placeholder(tf.float32) # mul = multiply 是将input1和input2 做乘法运算,并输出为 output ouput = tf.multiply(input1, input2) with tf.Session() as sess: print(sess.run(ouput, feed_dict={input1: [7.], input2: [2.]})) #placeholder到底像raw_input 呢还是argv呢
6,掰弯利器激励函数
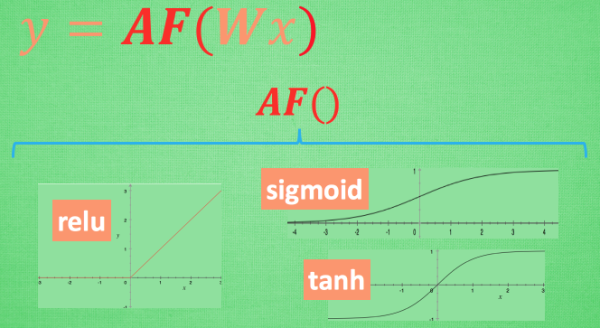
7,添加层
#!coding=utf-8 import tensorflow as tf
import numpy as np def add_layer(inputs, in_size, out_size, activation_function=None): Weights = tf.Variable(tf.random_normal([in_size, out_size])) biases = tf.Variable(tf.zeros([1, out_size]) + 0.1) #加0.1是为了不让它为0 Wx_plus_b = tf.matmul(inputs, Weights) + biases #最基础的函数:权重乘以x加上偏移量为y #如果激励函数为none,那我们得到的Wx_plus_b就是结果,如果有激励函数,那就需要把结果套上一层激励函数 if activation_function is None: outputs = Wx_plus_b else: outputs = activation_function(Wx_plus_b) return outputs
建造神经网络:
x_data = np.linspace(-1,1,300, dtype=np.float32)[:, np.newaxis] noise = np.random.normal(0, 0.05, x_data.shape).astype(np.float32) y_data = np.square(x_data) - 0.5 + noise #y=x的平方减去0.5加上干扰 #np.linspace意思的创建一个从-1到1的一维数组,这个数组里有300个元素,x_data的数字类型是float32。 #np.newaxis例如:print(np.arange(0, 10)[:, np.newaxis]) 结果将是[[0] [1] [2] [3] [4] [5] [6] [7] [8] [9]] #noise是故意插入数组中的干扰数字,省的算出权重和偏移量过快
xs = tf.placeholder(tf.float32, [None, 1])
ys = tf.placeholder(tf.float32, [None, 1])
#定义隐藏层,inputs为xs,大小为一个,经过10个隐藏层,激励函数为tf.nn.relu l1 = add_layer(xs, 1, 10, activation_function=tf.nn.relu) #输出层,输出层的输入值为l1,输入的值有10个,输出只有一层,激活函数是没有的 prediction = add_layer(l1, 10, 1, activation_function=None) #层虽然定义好了,我们仍旧需要通过训练优化参数,损失函数为,对二者差的平方求和再取平均。 loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - prediction), reduction_indices=[1])) #学习效率就等于 train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss) init = tf.global_variables_initializer() # 对变量进行初始化,然后会话中开始跑 sess = tf.Session() sess.run(init) #开始训练 for i in range(1000): # 注意当运算要用到placeholder时,就需要feed_dict这个字典来指定输入 sess.run(train_step, feed_dict={xs: x_data, ys: y_data}) if i % 50 == 0: # to see the step improvement print(sess.run(loss, feed_dict={xs: x_data, ys: y_data}))
训练得到的结果是loss损失的大小,损失越来越小,越来越接近实际值:
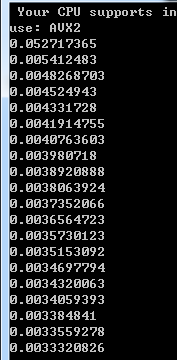
8,结果可视化
可视化需要用到的依赖包是:matplotlib,目测豆瓣和清华的镜像没法用,不知原因,直接按照教程来一遍吧。
实例:
#!coding=utf-8 import tensorflow as tf import numpy as np import matplotlib.pyplot as plt def add_layer(inputs, in_size, out_size, activation_function=None): Weights = tf.Variable(tf.random_normal([in_size, out_size])) biases = tf.Variable(tf.zeros([1, out_size]) + 0.1) #加0.1是为了不让它为0 Wx_plus_b = tf.matmul(inputs, Weights) + biases #最基础的函数:权重乘以x加上偏移量为y #如果激励函数为none,那我们得到的Wx_plus_b就是结果,如果有激励函数,那就需要把结果套上一层激励函数 if activation_function is None: outputs = Wx_plus_b else: outputs = activation_function(Wx_plus_b) return outputs x_data = np.linspace(-1,1,300, dtype=np.float32)[:, np.newaxis] noise = np.random.normal(0, 0.05, x_data.shape).astype(np.float32) y_data = np.square(x_data) - 0.5 + noise #y=x的平方减去0.5加上干扰 #np.linspace意思的创建一个从-1到1的一维数组,这个数组里有300个元素,x_data的数字类型是float32。 #np.newaxis例如:print(np.arange(0, 10)[:, np.newaxis]) 结果将是[[0] [1] [2] [3] [4] [5] [6] [7] [8] [9]] #noise是故意插入数组中的干扰数字,省的算出权重和偏移量过快 xs = tf.placeholder(tf.float32, [None, 1]) ys = tf.placeholder(tf.float32, [None, 1]) #定义隐藏层,inputs为xs,大小为一个,经过10个隐藏层,激励函数为tf.nn.relu l1 = add_layer(xs, 1, 10, activation_function=tf.nn.relu) #输出层,输出层的输入值为l1,输入的值有10个,输出只有一层,激活函数是没有的 prediction = add_layer(l1, 10, 1, activation_function=None) #层虽然定义好了,我们仍旧需要通过训练优化参数,损失函数为,对二者差的平方求和再取平均。 loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - prediction), reduction_indices=[1])) #学习效率就等于 train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss) init = tf.global_variables_initializer() # 对变量进行初始化,然后会话中开始跑 sess = tf.Session() sess.run(init) #开始训练 fig=plt.figure() #先生成一个图片框,画板类似的 ax=fig.add_subplot(1,1,1) #参数 111 的意思是: 显示一个图 或者写成 (1,1,1);参数 349 的意思是:将画布分割成 3 行 4 列,图像画在从左到右从上到下的第 9 块 ax.scatter(x_data,y_data) plt.show()
就目前而言,先把x_data ,y_data的取值画出来,x_data是在-1到1之间取了300个点,y_data是x_data的平方加上噪音,目前是这样的图:
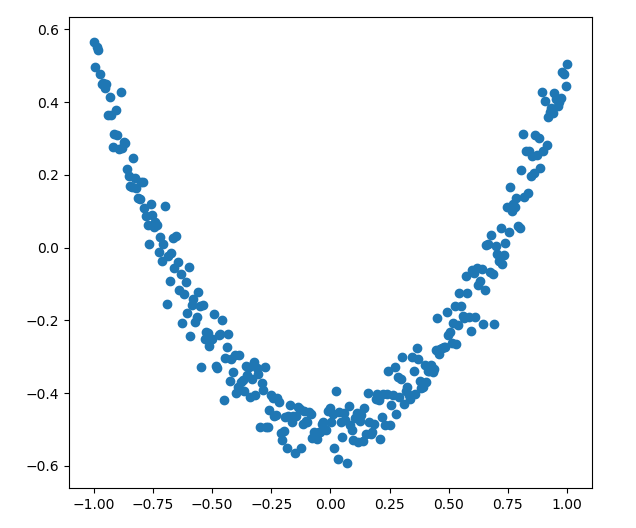
fig=plt.figure() #先 生成一个图片框,画板类似的 ax=fig.add_subplot(1,1,1) #参数 111 的意思是: 显示一个图 或者写成 (1,1,1);参数 349 的意思是:将画布分割成 3 行 4 列,图像画在从左到右从上到下的第 9 块 ax.scatter(x_data,y_data) plt.ion() #为了让画板能被不断更新添加,如果只有一个show()函数,那就只能画一次 plt.show() for i in range(1000): # 注意当运算要用到placeholder时,就需要feed_dict这个字典来指定输入 sess.run(train_step, feed_dict={xs: x_data, ys: y_data}) if i % 50 == 0: # to see the step improvement #print(sess.run(loss, feed_dict={xs: x_data, ys: y_data})) try: ax.lines.remove(lines[0]) #去掉画的第一条线,第一次没有这条线,所以except跳过去了 except Exception: pass prediction_value=sess.run(prediction,feed_dict={xs:x_data}) lines=ax.plot(x_data,prediction_value,'r',lw=5) #画一条连续的线,画完了必须要移除,否则画不了下一条 plt.pause(0.1)
虽然不是很懂,但是可以看到训练的结果确实是不断拟合原始数据哦。啦啦。至于为什么不大懂,估计是numpy和matplotlib包以前没用过的原因。
题外话,激活函数是可以变化的哦, tf.nn.sigmoid(x), tf.nn.relu(x),tf.nn.tanh(x), tf.nn.softplus(x)经过本人实践证明,同样的条件下,l1 = add_layer(xs, 1, 10, activation_function=tf.nn.softplus)是拟合最好的。据说它是这个: log(exp( features) + 1)



